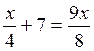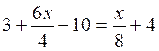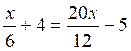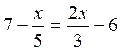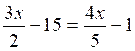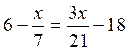Index warmaths	Liste des leçons
Ici _corrigé	DOC : Elève.

Leçon	Titre
N°7	Equation contenant une fraction de « x »

Ecritures :

Rappel 1: On ne peut pas additionner deux fractions qui n’ont pas le même dénominateur.

Rappel 2 :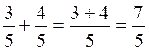

La somme de deux fractions de même dénominateur est égale à une troisième fraction qui aura pour numérateur « la somme des numérateurs » et pour dénominateur « le dénominateur commun ».

Rappel 3 :

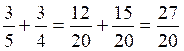
Pour faire l’addition de deux fractions de dénominateur différent il faut :

-Trouver un dénominateur commun (faire le produit des dénominateurs : ici 5 fois 4 =20)

- Réduire les fractions au même dénominateur , c’est à dire transformer chaque fraction en fraction équivalente de dénominateur égal à « 20 »

Tel que :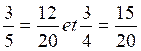

FIN des rappels 

COURS

Soit à résoudre l’équation :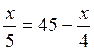

a) Rassemblons les « x » dans le premier membre On a :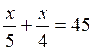

b) Faisons l’addition des deux fractions, après les avoir réduites au même dénominateur :

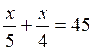Devient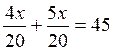

Soit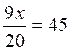

c) Calcul de « x » :

Nous calculons « x » :

- soit en passant par le produit en croix : 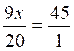; 9x = 900 ; x=100

-

- par la règle de trois :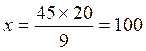

-

- Par une simple division :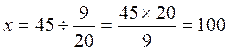

On retiendra : quand plusieurs termes en « x » sont « fractionnaires »,on les isole dans un membre. On effectue leur opération après avoir réduit au même dénominateur. Une règle de trois ou une simple division ou en passant par le produit en croix permet alors de calculer « x ».

Leçon	Titre
N°7	TRAVAUX d’AUTO - FORMATION sur Equations contenant plusieurs fractions de « x » .

TRAVAUX N° 7 d ’ AUTO - FORMATION : CONTROLE

Dans une équation qui comprend plusieurs fractions de « x » que faut-il faire ?

TRAVAUX N°7 d ‘ AUTO - FORMATION EVALUATION

Exercices : Résoudre les équations suivantes :

I)		· a
II)		· b
III)		· c

Pb 1: Deux cubitainers ont même contenance. Mais on vide le premier de ses 3/4 et le second de ses 4/5 , il reste dans le premier 6 litres de plus que le second. Quelle est la contenance de chaque cubitainer.

Pb2 : Un grand père donne successivement 1/3 puis 1/4 de sa fortune primitive à son petit-fils. Il compte qu’il donne ainsi 10 000 euros. Quelle était cette fortune ?

CORRIGE :

Exercices : Résoudre les équations suivantes :

IV)		· a
V)		· b
VI)		· c

Pb 1: Deux cubitainers ont même contenance. Mais on vide le premier de ses 3/4 et le second de ses 4/5 , il reste dans le premier 6 litres de plus que le second. Quelle est la contenance de chaque cubitainer.

Pb2 : Un grand père donne successivement 1/3 puis 1/4 de sa fortune primitive à son petit-fils. Il compte qu’il donne ainsi 10 000 euros. Quelle était cette fortune ?