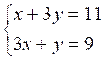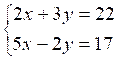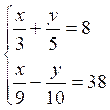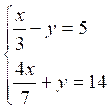|
|
|
DOC : Formation Individualisée |
DOC : Elève. |
|
ALGEBRE. N°
33 |
Information « TRAVAUX » ;Cliquer sur le mot !. |
|
OBJECTIFS :-
médiation en algèbre. |
I )
Pré requis:
|
i9 |
Le calcul numérique |
:i |
|
i9 |
Liste des objectifs
« passerelle » 3ème / Seconde. |
:i |
|
i9 |
:i |
II )
ENVIRONNEMENT du dossier :
|
Dossier suivant : 33 |
III
)
LECON n°32: Rectification d’énoncés. Problèmes à 2 inconnues.
IV)
INFORMATIONS « formation
leçon » :
|
|
Travaux auto - formation. |
|
Corrigé des travaux auto - formation. |
|||
V ) DEVOIRS ( écrits):
|
Devoir diagnostique L tests. |
|
|
Devoir
Auto - formatif (intégré
au cours) |
|
|
Devoir Formatif « Contrôle :
savoir » ; (remédiation) |
|
|
|
|
|
Devoir sommatif. |
|
|
Devoir certificatif : (remédiation) |
|
* remédiation :
ces documents peuvent être réutilisés ( tout ou
partie) pour conclure une formation .
|
Leçon |
Titre |
|
N°32 |
Rectification
d’énoncés. Problèmes
à 2 inconnues |
|
Rectification d’énoncés. Problèmes à 2 inconnues |
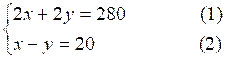
1° Problème :
Un élève rentrant de l’école explique à sa mère que la
coopérative scolaire se propose d’organiser une excursion. Le trésorier a reçu des propositions de deux
compagnies de transports automobiles. La première, qui prend 8 euros par
kilomètre parcouru et 10 euro par élève pour le déjeuner, demande 493 euros. La
deuxième demande 7,50 euros par kilomètre et 9 euros par élève pour le repas,
elle peut fournir un prix de 453 euros.
Le garçon, pour mettre
sa mère à l’épreuve, lui a demandé de
calculer combien d’enfants participent à l’excursion et quelle est la distance
parcourue.
La mère affirme, qu’il
y a une erreur dans l’énoncé. Pourquoi ?
Le garçon n’est pas
très sûr des prix globaux donnés par les sociétés de transports. Il sait que le
nombre de participants est « 25 » et que la distance est celle que la
mère a trouvée. Calculez les prix globaux et rétablissez le véritable système
des deux équations.
II) Solution.
Soit « x »
élèves et « y » kilomètres parcourus.
On peut écrire :
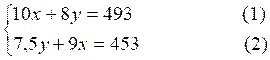
Nous multiplions les
deux membres de l’équation (1)
par « 9 » et ceux
de l’équation (2) par « 10 » :
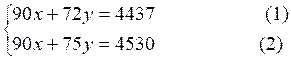
On opère la
différence : 3y =
4530 - 4437
3y = 93
D’où y = 93 : 3 = 31 ; La distance à parcourir est donc
de 31 kilomètres.
Portons cette valeur de
« y » dans l’équation (1) :
(8´ 31 )
+ 10x = 493
soit 248 + 10x = 493
10x = 493 - 248
10x = 245
D’où x = 245 : 10 ; x = 24,5
« x » étant
le nombre des participants ; il ne peut pas y avoir 24 participants et
demi.
Puisque nous savons
qu’il y a 25 participant et la distance est de 31 km, on peut écrire :
(10´ 25) + (8´ 31) = 498
(9´ 25) + (7,5´ 31) = 457,50
Ce qui donne le nouveau
système qui devrait être retenu :
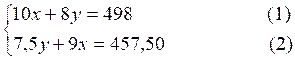
|
Algèbre :
Titre |
|
|
N°33 |
TRAVAUX d’Auto -
FORMATION sur Rectification d’énoncés. |
Reprise du contrôle de
l’objectif « 31 »
Compléter les phrases
suivantes :
I) Avant de choisir une
méthode de résolution que doit -on faire en présence du système ?
II) quand utilise- t-on la méthode par substitution ?
III) Donner la règle de procédure
permettant de résoudre un système à 2 inconnues par substitution :
1°) Raymond a entendu l’entrepreneur qui racontait ceci :
« J’avais des hommes sur un chantier. Je les payais 50 euros par
jour. Je n’en étais pas satisfait. J’ai
fait venir des spécialistes : je les paie 5 euros de plus par jour, et
bien qu’il y en ait 10 de moins ils m’ont fait le même travail avec une
économie de 255 euros ». Raymond ne
sait pas exactement combien il y avait d’hommes employés au début. Calculez-
le. Les données de Raymond sont- elles bonnes ? Pourquoi ?
Sachant que la deuxième équipe a touché 750 euros, rétablir l’équation
réelle et l’énoncé normal du problème.
2°) Dans une société de 12 personnes, on a fait une collecte. Chaque
membre honoraire a donné 10 euros et chaque membre actif 6 euros. La somme
totale est recueillie par un trésorier, qui, pour faire l’appoint, a mis de sa
poche un billet (qu’il croît être de 5 ou 10 euros). La somme totale recueillie
se monte à 109 euros. Peut-on rechercher le nombre de membres actifs, et le
trésorier peut- il savoir le montant du billet qu’il a donné en surplus ?
CORRIGE :
Résoudre :
Résoudre les systèmes suivants :
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
Problème :
1°) Raymond a entendu l’entrepreneur qui racontait
ceci : « J’avais des hommes sur un chantier. Je les payais 50 euros
par jour. Je n’en étais pas satisfait.
J’ai fait venir des spécialistes : je les paie 5 euros de plus par jour,
et bien qu’il y en ait 10 de moins ils m’ont fait le même travail avec une
économie de 255 euros ». Raymond ne
sait pas exactement combien il y avait d’hommes employés au début. Calculez-
le. Les données de Raymond sont- elles bonnes ? Pourquoi ?
Sachant
que la deuxième équipe a touché 750 euros, rétablir l’équation réelle et
l’énoncé normal du problème.
2°)
Dans une société de 12 personnes, on a fait une collecte. Chaque membre
honoraire a donné 10 euros et chaque membre actif 6 euros. La somme totale est
recueillie par un trésorier, qui, pour faire l’appoint, a mis de sa poche un
billet (qu’il croît être de 5 ou 10 euros). La somme totale recueillie se monte
à 109 euros. Peut-on rechercher le nombre de membres actifs, et le trésorier
peut- il savoir le montant du billet qu’il a donné en surplus ?