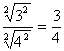|
Test suivant : |
|
|
Calcul NUMERIQUE |
SERIE N° 7: Niveau 3 |
-w-r-v- |
CORRIGE RACINES
|
TEST |
COURS |
Devoir
Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
Corrigé évaluation
|
Prérequis: Encadrement d' un résultat
|
SOS
Cours |
I ) remplacer dans les lettres par
les nombres suivants et faire le calcul :
avec
x= 16 et y =
9 (remarque : 16 et 9 sont des carrés
parfaits; nous connaissons la racine carrée de 16 (4) et de 9 (3) , ces valeurs
sont choisies pour faciliter la compréhension)
|
|
|
|
|
|
( |
( |
|
|
|
( |
( |
|
|
|
|
|
|
|
|
|
=
= 4
= 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Le calcul est impossible |
On ne peut faire la racine carré d'un nombre
négatif ! |
|
|
|
|
|
|
|
|
|
|
) 2
) 2
) 2
) 2 =162 = 256
=
=12
=
=
=
=
=
=
+
=
=
= 2,6457513
=
=
= "Erreur"
-II )
Transformer en vue de simplifier les calculs :
|
|
|
|
|
|
|
5 |
|
|
|
2 |
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + 4 =
7 |
|
|
|
|
|
|
|
=
3-4 |
|
|
( |
= 81 |
|
|
|
|
|
|
|
|
|
+
= 
) 2III)
Résoudre :
|
: 7 = |
7 2 = ( |
: 7 2 = 30+x 49 = 30+x 49 - 30 = x ;
19 = x ; conclusion « x » vaut 19 |
|
50 = |
50 2 = ( |
50 2 =1600+x2 2500 - 1600 = x2
30 = x |
|
|
|
|
|
|
|
|
CALCULS:
A )
Trouver les racines carrées parfaits des multiples de dixLmettre une croix dans la case correspondante
|
|
|
|
|
100 |
|
|
|
101 |
|
|
|
102 |
x |
|
|
103 |
|
|
|
104 |
x |
|
|
105 |
|
|
|
106 |
|
|
|
10 7 |
|
|
|
10 8 |
x |
|
B )
soit un nombre « x » ; trouver
la racine carrée du nombre :
|
|
|
|
|
x =0,25 |
|
0,5 |
|
x = 7,29 |
|
2,7 |
|
x = 33,64 |
|
5,8 |
|
x = 81 |
|
9 |
|
x = 291 600 |
|
540 |
|
x = 2 744 000 |
|
1656,502339 |
|
x = 1,5746 |
|
39681,22982 |
C
)Deuxième série d’exercices en relation avec la racne carrée d’un produit:
|
|
|
|
|
|
|
4 fois 5 =20 |
|
|
|
|
|
|
|
|
|
|
|
=630 |
|
|
|
=1600 |
|
|
|
=600 |
=20
=56
D )
Troisième série d’exercices en relation avec avec la racine d’un quotient:
Ces exercices utilisent des carrés parfaits
|
|
|
|
|
|
|
1,6 |
|
|
|
1,5 |
|
|
|
7 |
E ) Se
ramener aux carrés parfaits; en se souvenant que tout nombre « à
virgule » peut se mettre sous forme de fraction de dénominateur égal a
...........
|
|
|
|
|
|
|
9,3 |
|
|
|
0,86 |
=
F ) Quatrième série d’exercices en relation avec la racine carrée
d’une addition ou d’une soustraction ,
et les transformations
|
|
|
|
|
|
|
6,32455532 |
|
|
|
37,74917218 |
|
|
|
5,385164807 |
|
|
|
9,219544457 |
|
|
|
44,82186966 |
|
|
|
8,136952747 |
|
|
|
65 |
|
|
|
57 |
|
|
|
55 |
=
=
=
=
=
=
=
=
=G ) Cinquième série d’exercices: Donner une
valeur approchée d’une racine d’un nombre
1 ° ) Calculer les expressions suivantes avec la précision du dixième
|
|
|
|
|
|
|
2,2 |
|
|
|
4,1 |
|
|
|
69,0 |
2 ° ) Calculer les expressions suivantes avec la précision du centième
|
|
|
|
|
|
|
4,80 |
|
|
|
94,00 |
|
|
|
9,15 |
3 °) Calculer les expressions suivantes avec la précision du millième
|
|
|
|
|
|
|
9,434 |
|
|
|
9,7417 |
|
|
|
9,149 |
|
|
|
10,247 |
|
|
|
4,376 |
|
|
|
impossible |
H ) ENCADREMENT
D’UN RESULTAT :
On donne le résultat
des exercices suivants :
=4,4647451
=21,111276
=4,3742992
=4,717694
=2,6754054
= -3
Donner le résultat
sous la forme: n < 
< n +1
ou n est un entier naturel et X un nombre (entier ou décimal
)
|
: n |
< |
|
< |
n +1 |
|
4 |
|
|
|
5 |
|
21 |
|
|
|
22 |
|
4 |
|
|
|
5 |
|
4 |
|
|
|
5 |
|
2 |
|
|
|
3 |
|
-4 |
|
|
|
-3 |