Pré requis

 

La division euclidienne et division de N par 10 ;100;….1000 ;…

 

ENVIRONNEMENT du dossier:

 

Index   warmaths	Objectif précédent  92 Le dixième Le centième Le millième	Objectif suivant : 1° ) le nombre décimal 37a 2°)Le système métrique	Tableau        39 @ Liste des activités avec les nombres décimaux

39 DOSSIER   Relation  entre le nombre décimal   D

et la division d’un  N par 10 ou un multiple de dix

TEST	COURS	Devoir  Contrôle	Devoir évaluation	Interdisciplinarité		Correction évaluation  et contrôle

 

 

 

 Relation entre les  nombres D   sont  des « N »  divisés  par 10;100; 1000 …………………..et le système décimal

     Tel que  D à 1 chiffre après la virgule est égal à un  N : 10

                   Tel que  D à 2 chiffres après la virgule est égal à un  N : 100

                   Tel que  D à 3 chiffres après la virgule est égal à un  N : 1000          

 

 

COURS

 

 

 

Rappels :

 

*NOMBRE : un nombre est un alignement horizontal de chiffres..

*GRANDEUR : on appelle « grandeur »  un nombre associé à une unité.

 

* Le nombre sert à mesurer des « quantités ».   (quantifier)

 

*Le nombres décimal se compose de deux grandes parties séparées par une virgule:

 

La partie entière : devant la virgule

la partie entière est « découpée » de la même façon que les nombres entiers .appelée des « multiples de dix ». ( voir : numération d ’ un nombre entier)

La  partie décimale : derrière la virgule

                          La partie décimale : appelée sous multiple de dix

le premier chiffre après la virgule s’appelle : le  « dixième » (unité divisée en dix parties égales)

 le deuxième chiffre représente les centièmes d ‘ unité   ( voir les dixièmes de dixième )

le  troisième chiffre représente les millièmes d’unité ; ainsi de suite

 

 

Relation entre les  nombres D   et « N »

 

 Les entiers divisés par  10 ; 100 ; 1000 , donne les nombres décimaux  et permet de mettre en place le système décimal.

 

DIVISION DES NOMBRES ENTIERS PAR :                10 ; 100 ;1000 ; .....

 

 

Cette division s’apparente à la  division  d’un ensemble d’unités « 1 » contenant  « N » éléments ; nous effectuons un partage

pour obtenir des nombres décimaux :

 

Généralité : 

Le nombre décimal  peut se représenter sous la forme suivante :

 

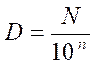
Rappels :

Soit le nombre « a »	« a » / 10	« a » / 100	« a » / 1 000
1	1/10 = 0,1	1/ 100 = 0,01	1 / 100 = 0,001
3	3 / 10 = 0,3	3 / 100 =  0,03	3 / 1000 = 0,003
23	23 /10  = 2,3	23 / 100 = 0,23	23 / 1000 = 0,023
567	576 / 10 =  56,7	567 / 100 = 5,67	0,567
2578	2578 / 10 = 257,8	25,78	2,578
69872	6987,2	698,72	69,872
124673	12467,3	1246,73	124,673

 

 

INVERSEMENT ; on peut dire qu’un nombre décimal peut être représenté par une fraction de dénominateur égal à 10 ; 100 ; ou 1000 , (ou multiple de dix )

Ainsi :

Cas de "1"  divisé par  10 ou un multiple de dix
0,1   =
0,01   =
0, 001 =

 

Autres  exemples  où  N est différent de 1  :

 

0,3   =	0,23   =	0, 567 =
1,3 =13/10	1,23 =123/100	1,564 = 1564/1000
21,3 =213/10	21,23 =2123/100	12,653 =12653/1000
721,3 =7213/10	821,54=82154/100	759,591 =759591/1000

 

 

 

Voir fraction représentant un nombre décimal

 

 

 

 

TRAVAUX AUTO FORMATIFS

 

CONTROLE :

 

Sous quelle forme peut-on représenter un nombre décimal ?

 

 

 

EVALUATION:

 

A partir des décimaux suivants : réécrire D sous forme fractionnaire correspondant à  la division de N par 10 ou un multiple de dix :

 

Exemple :                      D = N : 10   ( 1,3 = 13 :10 =  13 /10 )

 

1,3 =	1,23 =	1,564 =
21,3 =	21,23 =	12,653 =
721,3 =	821,54=	759,591 =