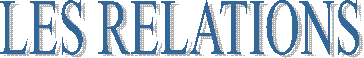Auteur : WARME R.

TRAVAUX  AUTO - FORMATIFS.

NOM : ………………………………

Prénom : …………………………..

Classe :…………………..

Année    scolaire : ………………………                                        

Dossier pris le : ……/………/………

Validation de la  formation :    O -  N

 Le : ……………………………………..

Nom du  formateur  : ……………………

ETABLISSEMENT : …………………………………………..

Les travaux auto formatifs sont destinés à préparer le devoir formatif .

Le devoir formatif  une fois passé  et validé  permet de passer les travaux certificatifs .( diplôme)

Leçon

TRAVAUX d ’ AUTO - FORMATION sur

N°22

LES RELATIONS TRIGONOMETRIQUES DANS LE TRIANGLE RECTANGLE

1°) Les angles ( désignations) .

Mots à placer :

AC.  ( ou CA ) ;  l’angle droit ; côté adjacent   ; Bêta ; alpha ; AB  ( ou BA ) ; consécutifs.

Pour le symbole « b » lire « …….. »

Pour le symbole « a »  lire « ……… »

En « A » : un carré (ou rectangle) symbolise ………………..

L’angle  « b » se trouve   à l’opposé  du côté ………. ( ou ……)

L’angle  « a »  se trouve  à l’opposé du  côté ……..  ( ou ………. )

Les côté AB et BC sont ……………. ; . ( AB est appelé le « ……………… » à l’angle « b »)

Les côtés AC et CB sont …………….. ( AC est appelé le « ……………….. » à l’angle « a »)

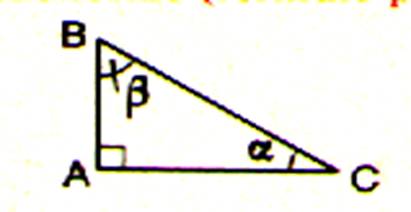
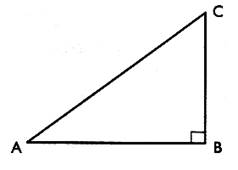
2°) Identification du « Côté opposé » , « côté adjacent » , « hypoténuse » d’un angle

Pour un triangle rectangle CBA ; rectangle en B :nommer  les côtés :

Compléter le tableau suivant avec les mots : Côté  opposé   ( à ) ; Côté adjacent (à ) ; côté adjacent  à 90° ; Hypoténuse ; Côté adjacent   ( à ) ; Côté opposé  ( à )

Si l’on se fixe sur un angle ; on nommera les côtés  de la façon suivante :

Pour l’angle droit

Pour l’angle    

Pour l’angle    

AC

est appelé :

AB

est appelé 

BC

est appelé 

3°) citer  les 3 principales relations trigonométriques sur le sinus , cosinus , tangente  ; donner le modèle  symbolique  mathématique.

4°)  Appliquer au triangle rectangle  ACB   les relations précédentes :

A quel rapport est égal ? :

 ;  ;      ;   ;  ;

5°) Passage d’une valeur décimale d’un sin a; cos a, tan a, à la valeur en degré de l’angle a

Compléter les phrases suivantes :avec les mots : en degré ; valeur décimale .

Lorsque l’on connaît la valeur décimale du sinus , du cosinus ou de la tangente d’un angle ,en consultant une table numérique  ou une calculatrice scientifique  obtenir  la valeur …………………… de cet  angle .

Inversement si je connais la valeur en degré de l’angle je peux obtenir avec la table numérique ou la calculatrice la ……………….. du sinus , cosinus ou  tangente de cet  angle .Le chapitre suivant aborde ce travail.

6°)    Détermination de la valeur décimale d’un sinus , cosinus et tangente à partir de la valeur  en degré de l’angle aigu. Compléter les phrases suivantes :

Avec les mots suivants :« grades ; degré décimal ; la calculatrice , degrés décimaux , ou radians . DEGRE ;ou une table numérique »

Les valeurs des rapports trigonométriques ( sinus , cosinus , tangente ) d’un angle aigu sont données par ………………………………………………..

Sur une calculatrice , les angles peuvent être exprimés en :………………………..………………………………………………………..

L’unité d’angle utilisé couramment  est le …………………………………...

7°) pour des calculs en trigonométrie il faut  mettre la calculatrice en mode………

8°)  Compléter le tableau ( voir votre calculatrice)

Pour trouver le sinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

  ……………

Pour trouver le cosinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

………………

Pour trouver la tangente sinus d’un angle aigu

Introduire  la mesure de l’angle  ( en degré)

Puis presser sur la touche

  …………………..

8°) mettre la calculatrice en mode  DEGRE

Détermination de la valeur de l’angle  en degré connaissant la valeur du sinus ou cosinus ou tangente avec la calculatrice :

Donner la touche remplissant la même fonction  sur votre calculatrice  :

    A partir de la  valeur décimale « sinus »  pour obtenir la valeur en degré  appuyer sur la touche :   INV . SIN ; ou  SIN^-1 ; ou ASN ; 

 A partir de la  valeur décimale « cosinus »  pour obtenir la valeur en degré  appuyer sur la touche  INV . COS ; ou  COS^-1 ; ou ACN ;  

 A partir de la  valeur décimale « tangente »  pour obtenir la valeur en degré  appuyer sur la touche  INV . TAN ; ou  TAN^-1 ; ou ATN ; 

9 °)Utiliser la calculatrice  pour trouver l’angle C dont le sinus est 0,876 5 , l’angle  A dont le cosinus est 0,423 6  et l’angle  C dont la tangente  est 1,973 2

 10 °) Compléter les phrases suivantes   sur les Calculs d’éléments d’un triangle rectangle :

avec les mots :  «  180° ; aigus ; Pythagore ; complémentaires ;( somme des 2 angles aigus) . »  

Dans un triangle rectangle si l’on connaît 2 côtés on peut avec « …………… » trouver la longueur du troisième coté . La somme des angles dans un triangle est de …………. .

La somme dans un triangle rectangle est de  …… = 90° + ………………………..

(ces deux angles aigus ,dont leur somme est de 90°, sont appelés :

                 angles ……………………….)

Dans un triangle rectangle , si je connais la longueur  de deux côtés , j’applique  « Pythagore » pour trouver la longueur du troisième côté.

                     Dans un triangle rectangle , si je connais la longueur  de deux côtés , je peux   calculer  le sinus ou  le cosinus ou la tangente  pour trouver la valeur d’un des angles ……………… .

TRAVAUX N° 22   d ‘ AUTO - FORMATION EVALUATION

1 °) Utiliser la calculatrice pour trouver le sinus , cosinus et tangente des angles : 7° ; 30° ; 84°.

Angle :

Sinus

Cosinus

Tangente

7°

30°

84°

( en général on arrondit au 0,001 près )

 2°)Utiliser la calculatrice  pour trouver l’angle C dont le sinus est 0,876 5 , l’angle  A dont le cosinus est 0,423 6  et l’angle  C dont la tangente  est 1,973 2

3°) En utilisant la calculatrice  ( donner le résultat arrondit à  0,000 1 près )

( a :lire angle alpha )

Angle a

0°

15°

30°

45°

60°

75°

90°

Sin a

Cos a

Tan a

4°) En utilisant la calculatrice , compléter le tableau ( arrondir à 0,1 près )

sina = 0 ,213 4

sina= 0,54 00

sina =0, 9687

L’angle a est égal à

Cos a = 0 ,213 4

Cos a= 0,54 00

Cos a =0, 9687

L’angle a est égal à

Tan a = 5 ,213 4

tana= 1

sina =0, 1187

L’angle a est égal à

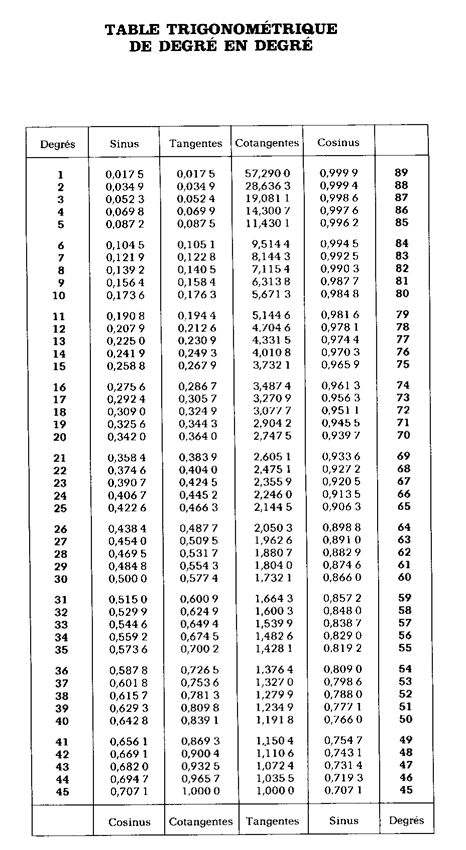
Utilisation  de  table   de trigonométrie .

3 °) « SINUS d’un angle »  :

A )Recherche du sinus à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

10°

24°

30°

45°

60°

90°

B ) Recherche d’ un angle à partir d’un nombre décimal (n £ 1 )

Avec la table.

Avec la calculatrice scientifique

0,2419

0,8290

0,289256198

0,5

0,866

4°) « COSINUS d’un angle »  :

A )Recherche du cosinus à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

10°

24°

30°

45°

60°

90°

B ) Recherche d’ un angle à partir d’un nombre décimal (n £ 1 )

Avec la table.

Avec la calculatrice scientifique

0,2419

0,8290

0,289256198

0,5

0,866

5° ) « Tangente d’un angle »  :

A )Recherche d’une tangente à partir d’un angle

Avec la table.

Avec la calculatrice scientifique

1°

10°

24°

30°

45°

60°

90°

B) Recherche d’ un angle à partir d’un nombre décimal

Avec la table.

Avec la calculatrice scientifique

0,2419

0,8290

0,289256198

0,5

0,866

1

12,56

19

57,2900

169

5067

12568

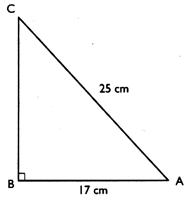
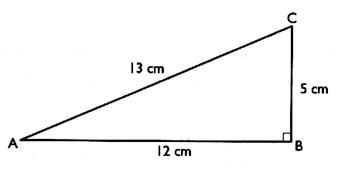
6°) On donne la longueur de l’hypoténuse et la longueur d’un côté  d’un triangle rectangle.

Que représente [CA ] et [BA] pour l’angle A ?.

Que représente [CA ] et [BA] pour l’angle C ?.

Calculs :

a) On demande de trouver la valeur de l’angle A , en degré .

b) En utilisant les relations trigonométriques trouver la valeur en degré de l’angle C.

Remarque : calculer la somme des angles   +    

Vérifier que  la somme des angles dans un triangle  est égale  à 180°

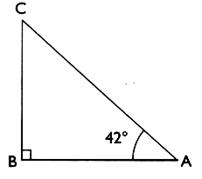
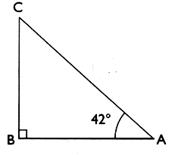
7°)  Calcul de la longueur d’un côté  connaissant un angle et la longueur d’un autre côté .

      Soit un triangle CBA rectangle en B .

      On donne l’angle A  = 42°  et  [B A]  = 20 cm.

Question : on demande de calculer la longueur du côté [ B C]  .

8°) :      Soit un triangle CBA rectangle en B .l’angle A  = 42°  et  [C A]  = 30 cm.

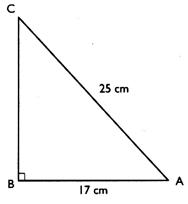
Question : on demande de calculer la longueur du côté [ B C]  .

9°)Dans le triangle rectangle ci - dessous : ( à vérifier par Pythagore )

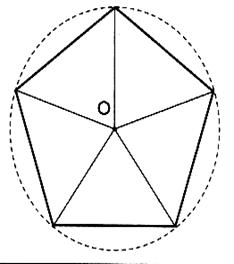
Calculer :   ;  ;   et puis  ,   et .

10°) On considère un pentagone  régulier inscrit dans un cercle de rayon 6 cm .

 a)Quelle est la nature  de chacun de ces cinq triangles dont le sommet  est le centre  "O" du cercle .

b)Donner une mesure de chacun de leurs angles . ( rappel :la somme des angles d'un triangle est de 180 ° )  . 

c)Calculer l'aire de ce pentagone . ( pour calculer  "h"  la trigonométrie) .

Angle :

Sinus

Cosinus

Tangente

7°

0,12186934340514

0,99254615164132

0,12278456090290

30°

0,5

0,86602540378443

0,57735026918962

84°

0,99452189536827

0,10452846326765

9,51436445422258