Pré requis : « @ PYTHAGORE
TRACES »
|
|
|
|
CALCULS de niveau 6 |
|
|
N°20 |
sur PYTHAGORE théorème ; la Propriété de
PYTHAGORE et sa réciproque. |
|
Pré
requis : a)
Que signifie l’expression « résoudre un triangle » ? b) Citer les deux méthodes qui permettent de
résoudre un triangle ? c) Citer les
possibilités permettant d ’ identifier les
caractéristiques d’ un triangle rectangle (mesures d’angle et de longueurs)
par le calcul. |
|
Niveau
référentiel : niveau 6 et
niveau V
Compléter
le tableau
|
|
|
Triangle 1 |
Triangle 2 |
Triangle 3 |
Triangle 4 |
Triangle 5 |
|
a |
|
37 cm |
5,3 cm |
0,65 m |
295 mm |
|
|
b |
450 mm |
35 cm |
45 cm |
0,56 m |
2,36 dm |
|
|
c |
600 mm |
120 cm |
280 mm |
0,33 m |
1,77 dm |
|
|
|
|
|
|
|
|
Série II
|
N°1 |
|
Données : |
Résolution : |
|
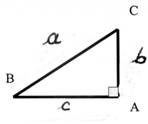
BA = 108 mm |
|
||
|
CA = 45 mm |
|
||
|
Calculer : |
|
||
|
« a » = ? |
|
|
N°2 |
|
Données : |
Résolution : |
|
|
|
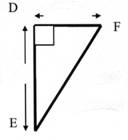
DF = 127 mm |
|
|
DE = 156 mm |
|
||
|
Calculer : FE
= x ; à 0,1 mm prés |
|
||
|
|
|
|
N°3 |
|
Données : |
Réponse : |
|
|
|
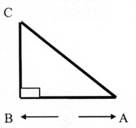
CA = 74 cm |
|
|
CB = 24 cm |
|
||
|
Calculer AB. |
|
||
|
|
|
||
|
|
|
Données : |
Réponse : |
|
|
|
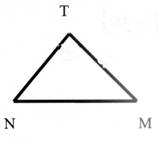
NM = 13,75
cm |
|
|
NT = 11 cm |
|
||
|
Calculer TM |
|
||
|
|
TM = 8,25 cm |
|
N°5 |
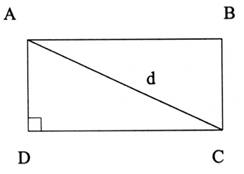
Application : Diagonale d’un rectangle |
Données : |
Résolution : |
|
|
|
AB = 170 cm |
|
|
BC = 95 cm |
|||
|
Calculer AC = « d » ( à 0,1 cm prés.) |
|||
|
|
|||
|
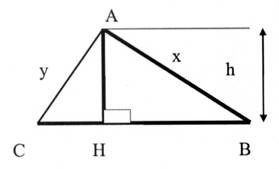
N°6 |
Triangle quelconque : |
Données : |
Résolution : |
|
|
|
CB = 114 cm |
|
|
HB = 71 cm |
|||
|
« h »
= 83 cm |
|||
|
Calculer : AB = x ( à 1 mm prés) AC = y (à 1
mm prés) |
|||
|
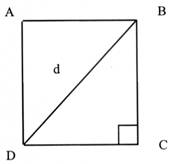
N°7 |
La diagonale d’un carré |
Données : |
Résolution |
|
|
|
BC = 32 dm |
|
|
En déduire
la valeur de AB ; CD ; AD. Calculer BD ( = d) à 1 cm prés. |
|||
|
7 b ++ |
Etudier le cas où
AB = 1 dm : d = racine de
2 |
|
d = 1 |
|
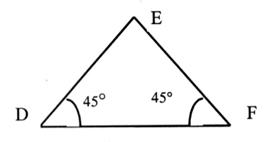
N°8 |
Le triangle
rectangle isocèle |
Données : |
Réponse : |
|
|
|
-Calculer l’angle E : -Quelle est la nature du triangle ? -DE = 160 cm En déduire
EF Calculer DF |
|
|
|
|||
|
|
|||
|
|
|||
|
8 b ++ |
Calculer DE
si DF
est égal à 6 cm |
|
|
|
N°9 |
|
Données : |
Réponse : |
|
|
|
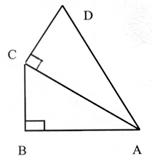
Sachant que DC = 31 m |
|
|
CB = 33 m
et BA= 56 m |
|
||
|
Calculer
AC ( à 0,1 m prés) |
|
||
|
|
|
||
|
N°10 |
|
Données : |
Réponse : |
|
|
|
En déduire l’angle C |
|
|
Que peut -on dire du
triangle ACB , au regard du triangle ADB ? |
|
||
|
Quelles sont les valeurs des angles : A CB = D C A = C D A = CAD = |
|
||
|
|
|
||
|
10 b +++ |
On donne AC = 60 , calculer
la valeur de AB puis BC |
|
|