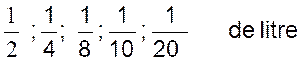LOGICIEL Pour Aide et Formation Individualisée		TRAVAUX INTERDISCIPLINAIRES		Pour aller directement aux informations « cours » voir cas par cas.
INFORMATIONS PEDAGOGIQUES :
►DOSSIER : Fractions et rationnels		Matière : MATHEMATIQUES		« Corrigé »
TITRE : TRONC COMMUN
Classe : Collège VIE QUOTIDIENNE. NIVEAU : niveau VI et V			OBJECTIFS : Travaux BILAN de fin de formation en vu d’obtenir une validation de la formation .
	I ) Pré requis: (pour remédiation ou mise à niveau)

TRAVAUX CONTROLE
Les questions relatives à « ce qu’il faut retenir » , c’est à dire ce qu’il faudrait « savoir » il faut se reporter aux cours .
TRAVAUX : EVALUATION
	N°1 :
	Un verre doseur utilisé en cuisine porte les graduations suivantes : On réalise avec ce récipient , un cocktail en mélangeant les quantités suivantes : litre de jus d’orange de litre de cognac de litre de liqueur d’orange de litre de sirop de sucre de canne. Quelle quantité obtient -on de cocktail ? ( écrire la réponse sous forme d’une fraction)  Ne pas utiliser la calculatrice , puis ensuite contrôler ce résultat avec celle -ci.
	N°2
	On dort huit heure par jour. Quelle fraction de la journée dort- on ? Quelle fraction de la semaine dort- on ? Quelle fraction de l’ année dort- on ?
	N°3
	2003 : La France a une superficie d’environ 550 000 km². La forêt occupe 1/ 5 du sol Les 2/ 3 de la forêt appartiennent a des particuliers. La superficie de la forêt a doublé en un siècle. a) Quelle fraction du sol français représentent les forêts privées ? b) Quelle est la superficie des forêts privées ? c) Trouver une question que l’on aurait pu poser
	N°4 : 1990 : L’Europe a une superficie de 10 200 000 km² La France a une superficie de 550 000 km². L’Europe des Douze ,dont fait partie la France , à une superficie de 3 260 000 km². a) quelle fraction de l’Europe des Douze occupe la France ? b) quelle fraction de l’Europe occupe l’ Europe des Douze ? c) Quelle fraction de l’Europe occupe la France ? Donner des fractions simples comme réponses.
	N°4 Deux cinquièmes des élèves de 3^ème passeront en 2^ème . Et 6 élèves sur 10 parmi les élèves de 2^ème n’auront pas leur bac. Sur 50 élèves en 3^ème , combien auront leur bac ? Et sur 100 élèves ?
	N°5 Un jour Claire dit à Luc , l’un des ces 8 enfants : voici une tonne de pommes de terre . J’en conserve le cinquième. Partage équitablement le reste avec tes frères et soeurs . Quelle masse de patates reçoit chaque enfant ?
	N°6 Pour préparer une confiture, on demande de suivre les proportions suivantes
		1. Variétés		2. Quantité de fruits à acheter		3. Quantité de jus préparé,		4. Quantité de sucre à ajouter.
		Coings et pommes		2, 000 kg		1 , 500 kg		1, 800 kg
	a) Quelle fraction du fruit constitue le jus ? b) Par quelle fraction doit-on multiplier la quantité de jus pour connaître la quantité de sucre à ajouter ? c) Compléter le tableau suivant :
								Vérifier si la recette est respectée
	(1)	Masse de fruits en kg.		2,5				5		100	1
	(2)	Masse de jus en kg.				7,5		3,80
	(3)	Masse de sucre.					10,80	5,5
	Calculs : passer de la ligne (1) à la ligne (2) et passer de la ligne (1) à (3)
	N°7 Pour un véhicule roulant à 90 km / h , la distance de freinage, dans de bonnes conditions , est de 50 m. La voiture bleue suit la voiture rouge à 15 m ; les deux véhicules roulant à 90 km/h. a) En une seconde , quelle distance (en m) parcourt une auto roulant à 90 km/h ? b) Un gros colis tombe d’un camion à 70 m devant la voiture rouge. Il s’écoule 3/4 de seconde avant que le premier conducteur ne freine. Apercevant les feux stop de la voiture rouge , le second conducteur a lui aussi un temps de réaction de 3/4 de seconde avant de freiner. 1- la voiture rouge aurait - elle pu s’arrêter à temps si elle n’avait pas été suivie ? la voiture aurait pu s’arrêter à temps 2- Mais la voiture rouge la suit . Expliquer ce qui va se passer .
	N° : Un avion décolle de Beauvais ; les 2/3 des sièges sont occupés. Après l’escale à Paris , on compte 21 passagers supplémentaires et l’avion est alors plein aux 3/4. Calculer le nombre de places assises de l’avion.