|
Leçon
|
Titre AUTO FORMATION. Série 1
|
|
N°10
|
Corrigé : Evaluation
PROPORTIONNALITE applications : Echelle ; pourcentage ;indice .
|
Problème
n°1 : Mesures sur un plan de maison. Sur le plan d'une maison, l'échelle est 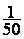 (ou 0,02). Quelle est
(ou 0,02). Quelle est
la
longueur réelle de la cuisine dont la
mesure sur le plan est 9 cm ?
Solution 1 :
|
On sait que : 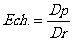 On pose On pose
|
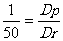
|
|
On transforme
|
1 Dr = 50 Dp
|
|
Dp = 9 cm , on remplace
|
Dr = 50 fois 9 cm
|
|
Conclusion
|
Dr = 450 cm
|
Solution 2 : Avec le tableau :
|
Mesure "réelle" en cm.
|
50
|
x (9 fois 50 = 450 cm)
|
|
Mesure plan en cm
|
1
|
9
|
Problème
n° 2 : Carte routière
Une carte routière est à l'échelle 1 : 50 000
(un cinquante - millième)
Rechercher par quelle mesure sera représentée sur la carte une portion de route droite longue de 3,5 km .
Solution1 : ( utilisation du
tableau)
On convertit en cm : 3,5 km = 3 500 m = 350 000
cm
On peut établir le tableau :
|
( x) Mesures
réelles en cm
|
50 000
|
350 000
|
|
(y) Mesure sur le plan en cm
|
1
|
"D p"
|
D’où 50 000 Dp = 1 fois
350 000 soit Dp = 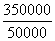 ; conclusion Dp = 7 cm
; conclusion Dp = 7 cm
Solution 2 :
|
On sait que : 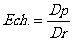 On pose On pose
|
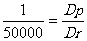
|
|
On transforme
|
1 Dr = 50 000 Dp
|
|
On sait que Dr =
350 000 cm , on remplace
|
350 000 = 50 000 Dp soit Dp = 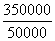
|
|
Conclusion
|
Dp = 7 cm
|
Problème N° 3 :
Agrandissement
Une plaque de métal
de 12 mm de long sur 6 mm de large
a été dessinée sur plan, le
rectangle tracé mesure 6 cm de long et 3 cm de large.
1°) Quelle est l'échelle
utilisée ?
2°) s’agit -il d’un agrandissement
ou une réduction ?(justifier)
3°) Donner l’équation linéaire ( que
représente « x » et « y »)
Solution :
On établit le tableau :
|
Mesures réelles en mm
|
12 mm
|
6 mm
|
|
Mesures "plans"
en mm
|
60 mm
|
30 mm
|
L'échelle
est le rapport 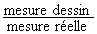 soit
soit 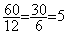 ;
;
-
l'échelle utilisée pour tracer le
plan est de "5"
Conclusion ::
- 2°) La
valeur du rapport de l'échelle est
supérieure à 1 ; il s'agit donc d'un
agrandissement.
3°)
l’équation linéaire est y = 5 x avec « x » = Dr , « y » = Dp
1°) Traduire en pourcentage : "je dépense 25 € sur
100 € ;
|
G1
|
156€
|
180 m
|
250 cl
|
956 kg
|
|
G2
|
15 €
|
18 m
|
25 cl
|
56 kg
|
|
A%
|
9,62 %
|
10 %
|
10 %
|
5,86 %
|
Problème :
Lors d'une période de soldes, un commerçant a affiché, pour
chaque article, le prix habituel et le
montant de la réduction accordée.
1°) Calculer le pourcentage de la remise pour chaque article.
2°) Quelle conclusion peut -on
tirer sur la valeur des remises.
|
Marchandise
|
prix habituel
|
réduction
|
|
Chemise
|
40 €
|
10 €
|
|
Pantalon
|
36 €
|
9 €
|
|
Veste
|
100 €
|
25 €
|
|
Polo
|
8 €
|
2 €
|
Solution :
1°) Pour vérifier qu'il y a proportionnalité, nous
allons calculer le coefficient de chaque marchandise ; pour déduire qu'il
existe un coefficient de proportionnalité "k".
On établit le tableau :
|
Prix normal
|
40
|
36
|
100
|
8
|
|
Montant de la réduction
|
10
|
9
|
25
|
2
|
|
calcul de « a »
|
10/40 = 0,25
|
9 / 36 = 0,25
|
25 / 100 = 0,25
|
2 / 8 = 0,25
|
|
« a
% »
|
0,25 fois 100 =
25 %
|
0,25 fois 100 =
25 %
|
0,25 fois 100 =
25 %
|
0,25 fois 100 =
25 %
|
Le coefficient est égal au rapport :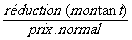
Chemise 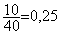 ;
Pantalon
;
Pantalon 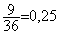 ; Veste
; Veste
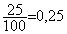 ; Polo
; Polo 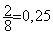
On constate que les
coefficients obtenus sont de même valeur
: 0,25
Le coefficient de proportionnalité est donc k = 0,25
On écrira :
Conclusion : la remise de tous les articles est
de 25%.
|
Soit les phrases suivantes
|
interpréter :
|
|
Un
mélange de peinture contient 10 % de
diluant
|
Pour 100 litres de peinture , il y aurait 10 litres de diluant
|
|
Un
commerçant réalise un bénéfice de 40 %
sur prix de vente.
|
Si le prix de vente était
de 100 € , le bénéfice serait de 40 €.
|
Problème
n° 2 :
On fait
une remise de 20% sur un meuble. Calculer la valeur de ce meuble sachant que la
valeur de ces 20 % représente 540 €.
Solution 1 :
Si la valeur du meuble était de 100 € la remise serait de 20
€.
|
Coût du
meuble
|
100
|
"x"
|
|
Remise
|
20
|
540
|
D’où la proportion : 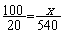 ;
;
En résolvant cette équation il vient : x = 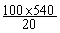 = 2700
= 2700
Donc le prix du meuble était de 2700 €
Problème n° 3 :
Un article dont le prix de départ est de
360 € est vendu avec une remise de 54 € sur le prix. Quelle serait la
remise pour 100 € marqué ?
Solution :
On établit un tableau :
|
Prix marqué
|
360
|
100
|
|
Remise
|
54
|
"x"
|
Proportion obtenue : 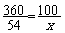
En résolvant cette équation il vient : 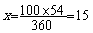
Le pourcentage de remise sur le prix marqué est de
15 %
Soit le tableau :
|
|
Base "100"
|
Réelle
|
|
Valeur
|
100
|
"x"
|
|
Remise
|
"a"
|
"y"
|
Expliquer comment on remplit ce
tableau,
|
Pour remplir ce tableau :
- On repère les grandeurs proportionnelles en transformant le pourcentage en une
comparaison: à "100" associe
"a" et à "x"
associe "y"
- On construit et l'on remplit le tableau afin d'obtenir la proportion :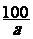 = = 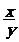
-On transforme
la proportion , pour obtenir un calcul à trois
nombres et on effectue les calculs
|
Problème
n°1 : En 2001, le
kilogramme de filet de bœuf est vendu
23,40 € ; en 2000 il était vendu 20 € ; à l'indice 100 .Trouver l'indice d'augmentation .
L'indice et le prix d'un produit sont des grandeurs
proportionnelles.
Solution :
|
|
An 2000
|
An 2001
|
|
indice
|
100
|
"x"
|
|
Prix au kg
|
20
|
23,40
|
L'indice est égale au
calcul :
Soit I
= 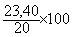 = 117
= 117
L'indice du prix en 2001 est de 117
.
L'augmentation en pourcentage du prix du kg de tomate est de : 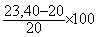 = 17
soit 17%
= 17
soit 17%
Problème
n° 2
1°) En l'an 2001, le
kilogramme du filet de viande de bœuf, est à l'indice 117 ; en 2000 il était à
l'indice 100 .
Dites ce que cela signifie :
Cela ne signifie pas qu'en l'an 2000 le kilogramme du filet de viande de
bœuf valait 100 € et qu'en 2001 il vaut 117 €.
2°) Le kg du filet de viande de bœuf valait 20 € à l'indice 100 ; en 2001 l’indice est de 117 . Quel est le prix du kilogramme du filet en
2001. :
il
vaut en 2001 : 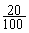
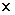 117 =
23,4 €
117 =
23,4 €
Compléter la phrase suivante : L'indice et le prix d'un produit sont
des grandeurs proportionnelles.
|
|
An 2000
|
An 2001
|
|
Indice
|
100
|
117
|
|
Prix au kg
|
20
|
23,40
|
3°)
calculer l’augmentation en pourcentage :
L'augmentation en pourcentage du prix du kg de filet de bœuf
est de : 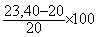 = 17
soit 17%
= 17
soit 17%
|
Leçon
|
EVALUATION (CORRIGE cliquer ici .)
|
|
N°10
|
TRAVAUX d ’ AUTO - FORMATION Résumé
Série 2 sur la PROPORTIONNALITE
applications : Echelle ; pourcentage ; indice .
|
ECHELLES :
|
1°) Sur une carte à l'échelle 1: 20 000, une portion de
route mesure 6,5 cm.
Calculer la longueur réelle de cette portion de route.
|
6,5 / Dr = 1 / 20 000
Dr = 6,5 fois 20 000
130 000 cm
= 1300m
|
|
2°) Le plan d'un appartement est à l'échelle 1:25 . la longueur
réelle de la chambre 1 est 4,50 m.
Calculer la mesure
à mesurer sur le plan.
|
Dp = 4;50 m :25 = 0,18 m
|
|
3°) Le dessin d'une pièce de monnaie est à l'échelle 4:3. S'agit - il d'un agrandissement
ou diminution ?
Calculer la mesure réelle du diamètre représenté
par 27 mm sur ce dessin.
|
4/3 = 27mm / Dr
Dr = 20,25 mm
|
4°) Dans chaque colonne
du tableau, on donne l'échelle et une mesure "plan". Calculer
les mesures réelles correspondantes.
|
Echelles
|
1 : 2
|
1 : 20
|
1 : 125
|
4 : 3
|
1 : 1000
|
3 : 1
|
|
Dr
|
30 mm
|
160mm
|
7750 mm
|
92,25mm
|
7000 cm
|
72 mm
|
|
D p
|
15 mm
|
8 mm
|
62 mm
|
123 mm
|
7 cm
|
24 mm
|
5°) Dans chaque colonne
du tableau, on donne l'échelle et une mesure "réelle". Calculer
les mesures "plan" correspondantes.
|
Echelles
|
1 : 2
|
1 : 20
|
1 : 125
|
4 : 3
|
1 : 1000
|
3 : 1
|
|
réelles
|
15 mm
|
8 mm
|
62 mm
|
123 mm
|
7 cm
|
24 mm
|
|
Plan
|
7,5mm
|
0,4 mm
|
0,495mm
|
164mm
|
0,007
|
72mm
|
B)
POURCENTAGE :
|
1°) calcul mental :
un
commerçant accorde à ses clients une réduction de 15 % sur le prix d'achat.
donner
dans chaque cas le montant de la réduction :
Pour 100 € l'achat la réduction sera de : 15 €
Pour 200 € l'achat la réduction sera de : 30 €
Pour 50 € l'achat la réduction sera de : 7,5 €
|
|
|
2°)
Calculer 24 % de 560 €
|
134,40 €
|
|
3°)
calculer 3,5 % de 500€
|
17,50€
|
|
4°) Le
prix d'un médicament est de 7,8 €. La sécurité sociale rembourse 75 % du prix
de ce médicament.
Calculer
le montant du remboursement.
|
5,85 €
|
|
5°) sur
une facture, les frais de transport représentent 8 % du prix de la
marchandise.
Ces
frais s'élève à 16 € , calculer le prix de la
marchandise.
|
16 = 8% x
x =
1600/8
x = 200€
|
|
6°) lors
d'un examen, 312 candidats ont été admis sur 520 inscrits.
Calculer
le pourcentage d'admis sur le nombre d'inscrits.
|
312 = (a
/ 100) x 520
31200 / 520 = 60
a=60 donc a%= 60%
|
|
7°) un
ouvrier gagnait 1256 € par mois, son salaire va être augmenté de 4 % .
Quel est
le montant de l'augmentation ?
et son
nouveau salaire.
|
Augmentation = 50,24 €
Nouveau salaire :
1306,24 €
|
C) INDICE . ( SOS info.) + corrigé « évaluation »
SUJET :
8°) Un objet coûtait 2500€ en janvier 1995 ; son
prix est passé à 2550 € en 1996 ,
puis à 2680 € en 1997 ; 2720 € en 1998 et 2750 € en 1998.
En prenant
pour base 100 en 1995 , calculer l'indice du prix de
cet objet , arrondi à l'unité , pour les 4 années suivantes .
9°) Le propriétaire d'un appartement utilise le tableau ci -
dessous pour calculer le loyer de l'appartement qu'il met en location
. Le loyer de cet appartement était en 1994 de 2850 €
.
Calculer
le montant du loyer pour les 3
années suivantes .
|
Année
|
Indice 4ème
trimestre
|
|
1994
|
1019
|
|
1995
|
1013
|
|
1996
|
1046
|
|
1997
|
1068
|
Pour les
problèmes suivants , on donne la formule suivante : 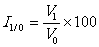
10°) Le
prix du litre d'essence était à l'époque
to de 1,75 € ; il est de 2,35 € à l'époque tn .Quelle est l'évolution du prix de l'essence ( en indice) ?
11°) A une
date donnée ( t1), un objet était vendu
3020 €.
Un objet
de même type vaut 2490 €. 8 ans plus tard (t2) .Donner l'indice
d'évolution du prix ( diminution ou augmentation)
CORRIGE
Evaluation : Leçon @: Les
indices simples :
Appelés: " indice simple
" , ou "indice analytique" ,
ou « indice élémentaire » ,
« indice particulier » :
Ij/o = 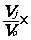 100
100
1°) Le
prix du litre d'essence était à l'époque
to de 1,75 € ; il est de 2,35 € à l'époque tn .Quelle est l'évolution du prix de l'essence ( en indice) ?
Solution :
calcul de l’indice :
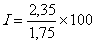 = (
134,28…..) soit I = 134
= (
134,28…..) soit I = 134
2°) A une
date donnée ( t1), un objet était vendu
3020 €.
Un objet
de même type vaut 2490 €. 8 ans plus tard (t2) .
Donner
l'indice d'évolution du prix ( diminution ou
augmentation)
Solution :
calcul de l’indice :
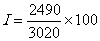 = (
82,450…..) , soit
I = 82
= (
82,450…..) , soit
I = 82
Puisque I < 100 , Il s’agit d’une diminution
3°) une
entreprise a payé à l'époque to une matière première "x" , 30 € le kg;
trois ans plus tard ( en t 3
) elle la paye 36 € le kg. Quel est
l'indice d'évolution ? Quel est le
taux de cette évolution ?
Solution I
= 100 ( 36
/ 30 ) ; I =
Le
taux de cette évolution est
de :
4°) Le loyer d'un
appartement était de 281, 4 € en 1992 pour un indice de 1005.
Question : On cherche le
montant du loyer en 1997 , l'indice étant de 1068.
On
complète le tableau de proportionnalité :
|
|
Année 1992
|
Année 1997
|
|
Indice
|
1005
|
1068
|
|
Prix
|
2 81,4 €
|
"x"
|
On
sort la proportion : 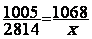 ; on
transforme "x" =
; on
transforme "x" =
"x" = 299,04 €
5°)
En 1998 , le prix d'un poste de télévision était 3200 € . Le prix en 2001 est de 3328 €
. En prenant pour base 100 l'année 1998 ,
chercher l'indice du prix en 2001.
On
complète le tableau de proportionnalité :
|
|
Année 1998
|
Année 2001
|
|
Indice
|
100
|
"x"
|
|
Prix
|
3200 €
|
3328 €
|
On
sort la proportion : 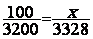 ; on
transforme "x" =
; on
transforme "x" = 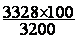
"x" = 104 ; l'indice est de 104
A)
ECHELLES :
|
1°) Sur
une carte à l'échelle 1: 20 000, une portion de route mesure 6,5 cm.
Calculer
la longueur réelle de cette portion de route.
|
|
|
2°) Le
plan d'un appartement est à l'échelle 1:25 . la longueur réelle de la chambre 1 est 4,50 m.
Calculer
la mesure à mesurer sur le plan.
|
|
|
3°) Le
dessin d'une pièce de monnaie est à l'échelle 4:3;
S'agit - il d'un agrandissement ou diminution ?
Calculer
la mesure réelle du diamètre représenté par 27 mm sur ce dessin .
|
|
4°) Dans
chaque colonne du tableau
, on donne l'échelle et une mesure "plan" . Calculer les
mesures réelles correspondantes.
|
Echelles
|
1 : 2
|
1 : 20
|
1 : 125
|
4 : 3
|
1 : 1000
|
3 : 1
|
|
Plan
|
15 mm
|
8 mm
|
62 mm
|
123 mm
|
7 cm
|
24 mm
|
|
réelles
|
|
|
|
|
|
|
5°) Dans
chaque colonne du tableau
, on donne l'échelle et une mesure "réelle" . Calculer les
mesures "plan" correspondantes.
|
Echelles
|
1 : 2
|
1 : 20
|
1 : 125
|
4 : 3
|
1 : 1000
|
3 : 1
|
|
réelles
|
15 mm
|
8 mm
|
62 mm
|
123 mm
|
7 cm
|
24 mm
|
|
Plan
|
|
|
|
|
|
|
B )
POURCENTAGES
|
1°)
calcul mental :
un
commerçant accorde à ses clients une réduction de 15 % sur le prix d'achat .
donner dans
chaque cas le montant de la réduction :
Pour 100 € l'achat la réduction sera de :
Pour 200 € l'achat la réduction sera de :
Pour 50 € l'achat la réduction sera de :
|
|
|
2°) Calculer 24 % de 560 €
|
|
|
3°) calculer 3,5 % de 500€
|
|
|
4°) Le prix d'un médicament est de 7,8 €
. La sécurité sociale rembourse 75 % du prix de ce médicament
.
Calculer le montant du remboursement.
|
|
|
5°) sur une facture, les frais de transport représentent 8
% du prix de la marchandise.
Ces frais s'élève à 16 € ,
calculer le prix de la marchandise.
|
|
|
6°) lors d'un examen, 280 candidats ont été admis sur 520
inscrits.
Calculer le pourcentage d'admis sur le nombre d' inscrits.
|
|
|
7°) un ouvrier gagnait 1256 € par mois, son salaire va
être augmenté de 4 %.
Quel est le montant de l'augmentation ? et son nouveau
salaire.
|
|
C) INDICES
8°) Un objet coûtait
2500€ en janvier 1995 ; son prix est passé
à 2550 € en 1996, puis à 2680 € en 1997 ; 2720 € en 1998 et 2750 € en 1998.
En prenant pour base 100 en 1995, calculer l'indice du prix de
cet objet, arrondi à l'unité, pour les 4 années suivantes.
9°) Le
propriétaire d'un appartement utilise le
tableau ci - dessous pour calculer le loyer de l'appartement qu'il met en location . Le loyer de cet appartement était en 1994 de 285
€.
Calculer le montant
du loyer pour les 3 années
suivantes.
|
Année
|
Indice 4ème trimestre
|
|
1994
|
1019
|
|
1995
|
1013
|
|
1996
|
1046
|
|
1997
|
1068
|
Pour les problèmes suivants , on donne la formule suivante : 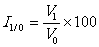
10°) Le prix du litre d'essence était à l'époque to de 1,75 € ; il est de 2,35 € à l'époque tn .Quelle est l'évolution du prix de l'essence ( en indice) ?
11°) A une date donnée ( t1),
un objet était vendu 3020 €.
Un objet de même type vaut 2490 €. 8 ans plus tard (t2) .
Donner l'indice d'évolution du prix (
diminution ou augmentation).
![]() (ou 0,02). Quelle est
(ou 0,02). Quelle est ![]() ; conclusion Dp = 7 cm
; conclusion Dp = 7 cm![]() soit
soit ![]() ;
;![]()
![]() ;
Pantalon
;
Pantalon ![]() ; Veste
; Veste
![]() ; Polo
; Polo ![]()
![]() ;
; ![]() = 2700
= 2700![]()
![]()
![]() = 117
= 117 ![]() = 17
soit 17%
= 17
soit 17%