i

Leçon	CORRIGE  des  TRAVAUX D’ AUTO FORMATION CONTROLE Série 1
N°9	LA PROPORTIONNALITE   et les calculs sur la proportionnalité ; son  l’application linéaire .

 

 

I) Rapport :

  Compléter la phrase : On appelle « rapport » : le quotient obtenu par la division d’un nombre par un autre nombre.

Compléter la phrase : Le modèle mathématique d’un « rapport » est « une écriture fractionnaire ou une fraction ».

Quelle est la forme  du quotient ?

Le quotient peut - être un nombre entier  un nombre décimal ; ou une fraction irréductible  dit « rationnel »

 

 

II ) Rapports égaux :

 

   Compléter la phrase : On appelle « rapports égaux » des divisions  qui ont le même quotient et dont le reste des divisions est nul .

 

- Compléter la phrase : Le modèle mathématique de deux rapports égaux est l’égalité de deux fractions.

 

 - Donner le modèle mathématique : le modèle   mathématique  est  :

 

III ) Suite de rapports égaux : 

 

1°) Compléter la phrase :   Lorsque nous avons plus de deux rapports égaux  nous pouvons  dire que nous avons  une « suite de rapports égaux » , le quotient de chaque rapport étant identique , c’est un nombre dit « constant » appelé « k ».

2°) Donner la traduction en langage mathématique :

                                               

 

 

 

 

 

 

 

 

 

 

I.      Suites de nombres  proportionnelles

 

1° )  Donner la définition d’ une suite de nombres  proportionnels :

 

2°)  Donner la procédure permettant de vérifier si deux suites de nombres forment une suite de nombres proportionnels.

Pour vérifier si  deux suites de nombres  forment une suites de nombres proportionnels  on  effectue  une simplification des rapports , on montre que les rapports  on le même quotient.

II.                Proportion

1°) Donner la définition d’une proportion :

Une proportion est l’égalité de  deux rapports.

2°) Soit l’égalité :    , donner un nom à cette égalité. : une proportion

  3°) Soit l’égalité :     : que peut - on dire des produits  a   d   et   c  b  

Dans une proportion les produits   a   d   et   c  b   doivent être  des produits  égaux : «  24 » .

4°)  Comment  appellent  -on ces produits :  a   d   et   c  b    ?

Les produits  de  a   d  et  c  b  sont  appelés "les produits en croix".

4°)   Dans la proportion   ;dont on veut appliquer le produit en croix , comment appelle- t  - on   les lettres représentant les  nombres  « a » et « d »   et  les nombres  « b » et « c » ?

les nombres  « a » et « d »   sont appelés "les extrêmes"  et  les nombres  « b » et « c » sont appelés "les moyens".

5°) Compléter la phrase suivante : 

 Dans une proportion le produit des extrêmes est égal au produit des moyens.

6°)  On dit que dans une proportion les deux fractions sont équivalentes.

Comment peut-on vérifier si les deux fractions sont équivalentes ?

Deux fractions sont équivalentes si le produit du numérateur de la première fraction par le dénominateur de la seconde fraction est égal au produit du numérateur de la deuxième fraction par le dénominateur de la première fraction.

 

 

7°) A quelle condition peut -on dire que les fractions suivantes  sont - elles  équivalentes ?

 

Les fractions sont équivalentes si le produit en croix    ad = c b   est vérifié

III.     Coefficient de proportionnalité

 

1°) Compléter la phrase :   Le coefficient de proportionnalité est un nombre.

2°) Quand dit  - on  que le coefficient de proportionnalité existe ? Ce nombre, appelé : coefficient de proportionnalité, existe  lorsque  l’on  multiplie chaque valeur  de la première  suite pour donner les valeurs correspondantes de la seconde suite.

´ 2	¯	1,5	4,3	9,6	Donner le nom de cette première ligne : Dans cette   Ligne supérieure  les nombres forment la    « Première suite »	¸2  ­
		3	8,6	19,2	Donner le nom de cette ligne : Dans cette   Ligne inférieure   les nombres forment la    « seconde suite »

Vérifications :   On a bien   4,3   2 =  8,6     et     9,6  2 = 19,2

3°) a quoi est égale le coefficient  de proportionnalité 

Le coefficient de proportionnalité est égal au rapport des nombres de la deuxième suite aux nombres correspondants de la première  suite.

 

 

 

IV.               Proportionnalité et « l ’équation » :   y = a x  ( représentante  de  la fonction dite « linéaire » )

 

La fonction linéaire est le modèle algébrique  permettant de traiter  toutes les situations  problèmes de la proportionnalité.

 

V.      Tableau de proportionnalité

 

Compléter   tableau  de proportionnalité :  soit « a » le coefficient de proportionnalité ;

	x	x1	x2	x3	x4	x5	x6
	y	ax1	ax2	ax3	ax4	ax5	ax6

 

VI.  Recherche du coefficient de proportionnalité

Soit le tableau de  proportionnalité , montrer comment on obtient le coefficient de proportionnalité :

x	x1	x2	x3	x4	x5	x6
y	ax1	ax2	ax3	ax4	ax5	ax6

 

On  effectuera les calculs suivants :  ax₁ / x₁  = ax₂ / x₂  = ax₃ / x₃  = ax₄ / x₄  = ax₅ / x₅  = …= a

 

VII. Représentation graphique  d' une proportion

1°) Quelle est la représentation graphique d’une situation de proportionnalité ?

La représentation graphique d'une situation de proportionnalité est une droite qui passe par l'origine.( O ) du repère.

 

IX)  Application linéaire .

:

·   «  k »  est un nombre non nul (  ou  on dit aussi :   différent de 0 ;  ¹ 0) 

· L’application linéaire de coefficient « k » fait correspondre à chaque nombre « x » le nombre  «  k ´  x ».

on notera  le  calcul  de  k ´ x = y    soit  l’équation :   y = k x   ,

où   on dira  que le produit  de  « k x »  est l’image  de « x » par l’application linéaire de coefficient « k » . On dira donc   que  «  x  à pour image   k x »

«  x  à pour image   k x » : on notera cette phrase par l’écriture symbolique :     x    k x

· Si l’application linéaire s’appelle «  f » et  si « y » est l’image de « x »

 on notera   y =    f (x)

 

 

 

 

2°) Application linéaire liée à une situation de proportionnalité. :

On donne  :    x  a x ;  compléter le tableau de proportionnalité

« a »	x	x1	x2	x3	x4	x5	x6
	y	ax1	ax2	ax3	ax4	ax5	ax6

3°) Représentation graphique

Compléter la phrase : La représentation graphique de l’application linéaire de coefficient « k » est la droite d’équation  y = k x

Elle passe  par deux points remarquables, lesquels ?

 Elle passe  par  le point  « O » ( 0 ;0)  et par le point « A » ( 1 ; k )

4°) Coefficient :

Soit  l’application linéaire   f   telle que  f ( x₁)  =  ( y₁) , donner le calcul  permettant d’obtenir le coefficient :       a =  (y₁) / x₁

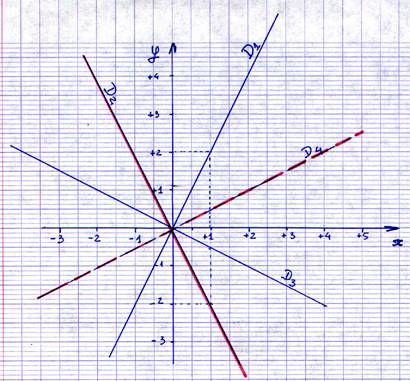
5°) Exemple de représentations graphiques :

La représentation graphique d’une fonction linéaire est une droite passant par « O ».     D1   ; D2 ; D3 ; D4   sont des droites passant par « O » Quel est le  signe du coefficient ? D1 = +  ; D2 = - ; D3 = - ; D4 = +