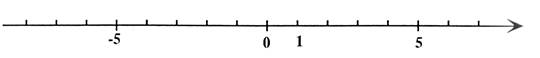|
LOGICIEL warmaths nivV. BEP Pour Aide et Formation Individualisée |
CORRIGE TRAVAUX
SOMMATIF B. E . P. |
Pour aller
directement aux informations « cours » voir cas
par cas. |
|||||
|
Devoir N° 3 / 15 |
Matière : MATHEMATIQUES |
||||||
|
|
|
||||||
|
|
|||||||
|
OBJECTIFS : Travaux BILAN de fin de
formation en vu d’obtenir une
validation de la formation . Peut être utilisé pour faire un
diagnostique. |
|||||||
|
|
I ) Pré requis: (pour remédiation ou mise à niveau) |
|
|||||
|
|
Voir le niveau CAP |
|
|||||
|
|
|
||||||
|
|
CONSIGNES |
||||||
|
|
La séquence ne doit pas dépasser 45
minutes. Matériel : le matériel habituel est autorisé :crayon ,
stylo, règle, rapporteur, compas,équerre, calculatrice. Ecrire à l’encre, dessiner
au crayon. (trait fin ,net , précis.) Feuille de brouillon. Le devoir est à rendre sur copie blanche. Ecrire les calculs et
encadrer la réponse. |
||||||
|
|
||
|
|
|
|
|
|
TRAVAUX CONTROLE |
|
|
|
|
|
|
|
Les
questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours
. |
|
|
|
|
|
|
|
TRAVAUX : EVALUATION |
|
|||||||
|
|
|||||||||
|
1. |
|
||||||||
|
|
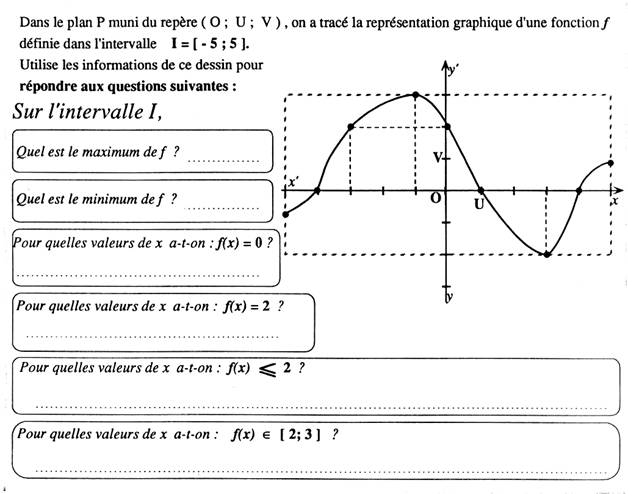
Maximum de f : 3 Minimum de f = - 3 f(x) = : - 4 ;
1 ; 4 f(x) = 2 ; 0 et
- 3 f (x) £ 2 : x Î [ - 5 ; - 3 ] È [ 0 ; 5 ) ] f (x) Î [ 2 ; 3
] ; réponse : x Î [ - 3 ; 0 ]
|
||||||||
|
2. |
|||||||||
|
|
Résoudre
l’inéquation : x - 1 <
4x + 5 Quel
est l’ensemble des solutions ? Utiliser
l’axe dessiné ci dessous pour représenter graphiquement l’ensemble des
solutions de cette inéquation. (préciser
comment il convient de lire votre représentation. (légende)). Réponse : x > -2 |
||||||||
|
|
|
||||||||
|
3. |
|||||||||
|
|
Construire
un triangle ABC tel que : AB =
2,5 cm ; AC = Mesurer
l’ angle A . Vérifier par le calcul.
Quelle est la nature du triangle ? |
||||||||
|
|
C’est un triangle qcq . Est -il rectangle ? On trace , on mesure l’angle A qui semble être égal à 90°. Vérifions si il peut être rectangle. |
« réciproque de Pythagore ». On calcule : 6,5² = ? 42,25 2,5 ² = ?= 6,25 6² = ? = 36 |
On remarque que : 6,5 ² = 2,5 ² + 6 ² D’après la réciproque de Pythagore : le triangle est
rectangle. |
||||||
|
|
On aurait pu utiliser la trigonométrie dans le triangle quelconque. (SOS cours) A savoir que : a² =
b² + c² + 2bc cos A ; Avec « a » le plus long côté . si 2
bc Cos A = 0 ; alors l’angle A est droit ; il y a un angle
droite : 90 ° |
||||||||
|
4 |
SOS
Cours |
||||||||
|
|
|
||||||||
|
|
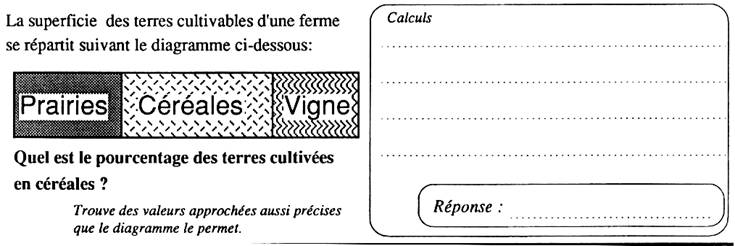
En valeur approchée on doit trouver , au sens large, entre
42,5 et 45 % 2 façons pour
calculer : 1°) calculer l’aire du
grand rectangle
« prairies-céréales-vigne » , calculer l’aire
« céréales » ; Voir le rapport proportionnel : 100 (A
céréale/ Aire totale ) = a% 2°) mesurer la longueur du
grand rectangle « L » ; mesurer la longueur (l) du rectangle
« céréales» puis faire le rapport
( l / L) 100 = a % |
||||||||
|
5. |
SOS cours 1 « arrondir » et SOS cours 2 « valeur
approchée ». |
||||||||
|
|
Donner
une valeur approchée au centième des nombres suivants : |
||||||||
|
|
|
Réponse
|
|
|
Réponse : |
||||
|
|
|
2,61 ou 2,62 |
|
|
0,78 ou 0,79 |
||||
|
|
4,09 ou 4,10 ou 4,1 |
|
|
12 |
|||||
|
6. |
SOS
cours 1 : Calcul des fréquences |
||||||||
|
|
SOS
Cours 2 : le diagramme à bâtons |
||||||||
|
|
|
||||||||
|
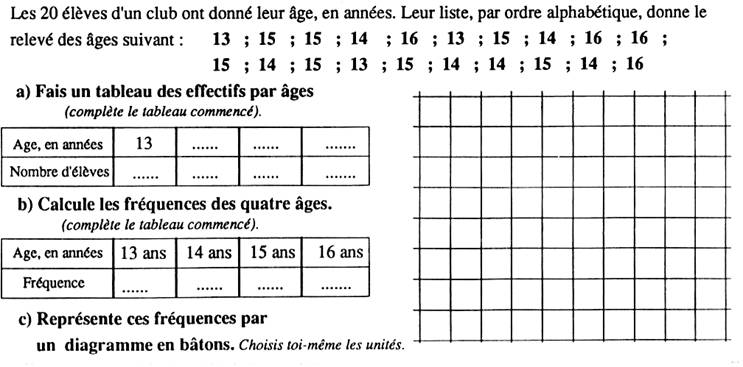
Réponse tableau « a » : 3 ; 6 ; 7 ;
4 Réponse tableau « b » : 0,15 ; 0,30 ;
0,35 ; 0,20 Diagramme : ce sont des bâtons de longueurs proportionnelles
aux effectifs , avec indication des fréquences. Fin du devoir 3 / 15 |
|||||||||