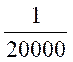|
|
|
|
|
|
DOSSIER : INTERDISCIPLINARITES Grandeurs proportionnelles et
Applications de la fonction linéaire. |
L’ OUTIL
MATHEMATIQUE de la fonction linéaire est de la forme : y = a x ou
y = m x
La variable « ![]() »
est multipliée par le coefficient «
»
est multipliée par le coefficient « ![]() »
ou «
»
ou « ![]() »
ou «
»
ou « ![]() »
s’écrit : :
»
s’écrit : : ![]() ou
ou ![]()
par convention le signe « multiplier »
n’est pas représenté entre deux lettres : ![]() ou
ou ![]() s’ écrira
s’ écrira ![]() ou
ou ![]()
Situations problèmes ,
|
Domaine
automobile |
|
|
Questions : Trouver les équations des droites .
(Donner la signification de y et x , le l’unité attribuée
) |
|
|
1 )Le
prix à payer est directement
proportionnel à la quantité de carburant : Pour du fuel 1,50 € /litre |
|
|
2 ) Un
automobile estime la consommation de son véhicule à Quelle peut être sa consommation pour : 50 km ; 150 km ; 200 km ;500
km ; « x » km |
|
|
3 ) Composant d’un alliage : Le duralumin contient 95 % d’aluminium , 4 %
de cuivre , 0,5 % de manganèse et 0,5% de magnésium. Quelle est la masse de chacun des composants contenue dans une masse
de 650 g de duralumin ? |
|
4 )On
recouvre une plaque de 1 m2 destinée à fabriquer des circuits
imprimés d’une couche de cuivre de 35 microns .La masse volumique du cuivre
est de 8,92 g . cm-3 Calculer la masse de cuivre utilisée. |
|
5 ) Un
garagiste accorde une remise suivant le tableau : Prix (€) x : 40 ;50 ; 80 ;250 ;430 Remise (€ )
y : 4 ; 5 ; 8 ; 25 ; 43 a)
peut-on mettre sous la forme y =ax la relation qui exprime la remise et le prix ? b)
tracer la droite représentant la fonction x |
|
6 ) La
vitesse de coupe d’une fraise est donnée par le tableau suivant : Vitesse de rotation en tours . min-1
( N) :250 ;
375 ; 500 ;125 Vitesse de coupe en m.min-1
(v) 11 ; 16,5 ; 22 ; 5,5 a)
peut –on mettre sous la forme y = an la relation
qui lie la vitesse de coupe à la vitesse de rotation ? représenter graphiquement la fonction n |
|
7 ) La
différence de potentiel V aux bornes d’un résistor et l’intensité I du
courant qui le traverse sont données par le tableau : V (volts) : 7,5 ; 10 ; 17,5 ; 30 ; 37,5 I (ampères) : 1,5 ;2 ;3,5 ;
6 ; 7,5 Peut-on mettre sous la forme V = a I la relation qui lie la différence de potentiel à l’intensité du
courant ? Représenter graphiquement la fonction I |
|
8 ) Un
ressort a 10 cm de longueur . Quand on y suspend
des poids , les allongement sont donnés dans le
tableau ci-dessous : Poids (N) : 10 ; 20 ;30 ;40 ;50
60 Allongement (mm) : 20 ; 40 ;60 ;
80 ; 100 ; 120 a)
Peut-on mettre sous la forme y = ax la relation qui exprime l’allongement du ressort et le
poids « x » ? Tracer le graphique de la fonction obtenue. b)
Trouver graphiquement l’allongement pour les
poids suivants : 15N ; 32,5N ;52
N ; 65 N Indiquer la longueur du ressort dans chacun de ces cas
. c)
trouver graphiquement le poids qui correspond à
un allongement du ressort de 36 mm , 72 mm , 110 mm
, 125 mm . Vérifier par le calcul les résultats trouvés . |
|
9 ) La
relation A(t) = l0at représente l’allongement d’une tige à la
température t à partir de la
longueur l0 à la
température 0°. L’allongement d’un rail mesurant 18 m à 0° est 6,5 mm à la température
de 30° C. a)
Calculer le coefficient de dilatation « a » de ce rail . b)
Représenter graphiquement la fonction : t c)
Déterminer graphiquement l’allongement du rail à
12°C , à 26°C. Vérifier par le calcul. d)
Déterminer graphiquement et par le calcul
l’élévation de température qui produit
un allongement de 1,1 mm ; de 4 mm. . |
|
10 ) Une
carte géographique est à l’échelle On désigne par « D » les distances réelles exprimées en
mètres et par « d » les distances
correspondantes mesurées sur la carte en mètres. a)
Ecrire la relation liant « D » à
« d ». b)
La fonction d Donner
sa représentation graphique lorsque « d » varie de 0 à 1 . |
|
11 ) Un
capital « x » (en € est
placé pendant un an au taux d’intérêt 5,4 % ( 100 f rapportent 5,4 € en un an ) .On rappelle que i = C tn ;
« n » est la durée du placement exprimée en années ) a)
Calculer l’intérêt produit si x = 10 000 € Exprimer l’intérêt produit « y » en fonction de
« x ».représenter graphiquement la fonction x |
|
12 ) Une
banque attribue 10% d’intérêt . a) Quel est le montant de
l’intérêt perçu au bout d’un an si je place 5000 € ? b)
Donner la formule qui permet de calculer l’intérêt annuel
« I » en fonction du capital
C. Déterminer la fonction linéaire associée à cette situation. |
|
13
) Considérons un robinet dont le
débit est de 20 litres par minute. a)
Construire un tableau et compléter ce
tableau : Temps t (min) 1 ;
2 ; 5 ; 8 ; 10 ;12 Quantité d ‘eau « q » (litres) 20 ; x ;y ;
z ;t ;v On passe du temps « t » (min) à la quantité « q »
(litres) par la fonction linéaire t Tracer
la représentation graphique de cette fonction lorsque « t » varie
de 0 à 20 . (Echelles : sur Ox , 1 cm = 2 min ; sur Oy ,
1 cm = 40 litres) |
Des connaissances e
n sciences sont nécessaires pour comprendre le travail
demandé ; (à vous de vous
informer :
14°) Calculer la mesure de la d.d.p. aux bornes d’un résistor dans les cas
suivants :
|
calibre |
Echelle |
lecture |
d.d.p |
|
3 V |
[ 0 ;
30 [ |
22
divisions |
|
|
10 V |
[ 0 ;
100 ] |
57
divisions |
|
|
300
V |
[ 0 ;
30 [ |
25
divisions |
|
15°) Quelle est l’intensité du courant
traversant le circuit ?
|
Calibre |
Echelle |
lecture |
|
1 A |
( 0 ;
100 ) |
83
divisions |
|
0,1
A |
( 0 ;
100) |
57
divisions |
16°)
Une voiture consomme 18,4 litres
d’essence pour effectuer le trajet Paris - Caen ( 230 km) .Quelle
sera sa consommation pour effectuer le trajet
Paris - Cherbourg long de 340 km ?
Que devons nous
admettre pour résoudre le problème ?
17°) La masse et le volume d’un corps
sont deux grandeurs directement proportionnelles .Le coefficient de
proportionnalité s’appelle la « masse volumique » du corps.
a) Calculer
le volume d’un corps de masse 52 kg dont
la masse volumique est de 23 kg /dm3
b) Calculer
la masse d’un corps de volume 3,5 dm3 dont la masse volumique est de
7,8 kg / dm3.
18 ) La longueur du cercle est donnée en
fonction du diamètre ; compléter le
tableau suivant :
|
D |
5 |
10 |
12 |
25 |
28,2 |
|
L |
|
|
|
|
|
Les deux grandeurs sont-elles proportionnelles ?
19 ) Un
cycliste parcourt 12km en 45mn .Un autre 17km en 50mn .Les distances parcourues
sont-elles directement proportionnelles
aux durées du parcours ?
20 )
Construire un triangle ABC dans
lequel BC = 50mm , l’angle B =40° et l’angle C =50°
Mesurer les cotés et les angles. Les mesures
des cotés sont-elles proportionnelles aux mesures des angles opposés ?
21 ) Même question pour un triangle ABC tel
que l’angle A = 60° , l’angle B = 30° ,AB = 70 mm
22 )
Une voiture se déplace à la vitesse constante de 80 km.h-1
.La distance parcourue est-elle proportionnelle à la durée du parcours ?
23 )
Le vernis au tampon est une opération qui permet d'appliquer sur le bois
finement préparé une pellicule de vernis mince et transparente ayant le poli
d'une glace.
La recette la plus simple de
vernis consiste à diluer environ une masse donnée de gomme-laque en paillettes
dans de l'alcool. Le tableau suivant rassemble la masse en grammes de
gomme-laque pour des préparations nécessitant un volume d’alcool en litres
donné.
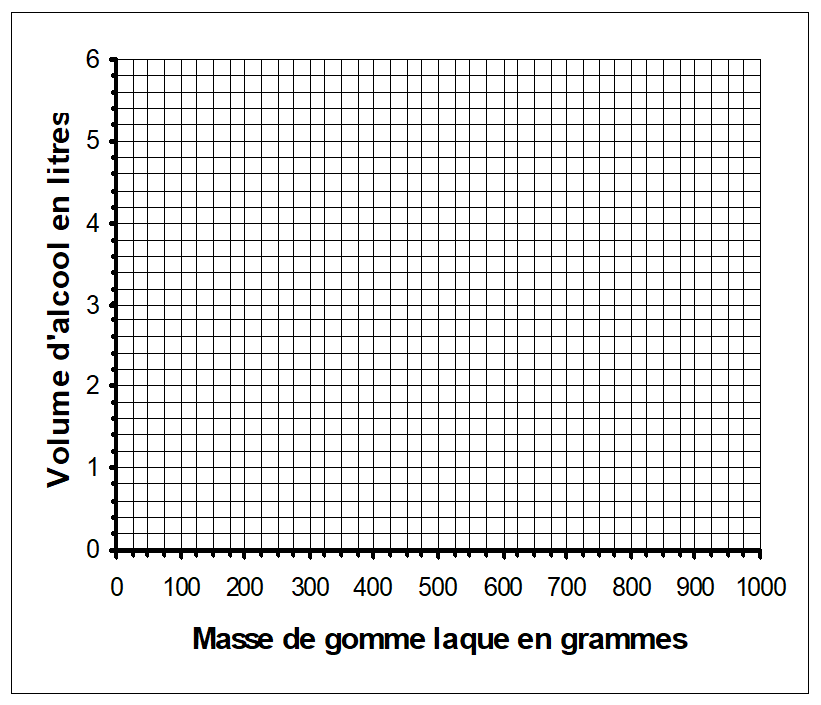
|
Masse de gomme laque (en
grammes) |
175 |
350 |
525 |
700 |
875 |
|
Volume d’alcool (en litres) |
1 |
2 |
3 |
4 |
5 |
1°) Compléter le graphique donné en annexe.
2°) Quel est le type de courbe
représentée par ces points ?
3°) Les deux grandeurs sont-elles
proportionnelles ? Justifier la
réponse
4°) Par une lecture graphique, en laissant les traits de constructions
apparents, déterminer la masse de
gomme laque à diluer dans un volume d’alcool de 2,5 litres.
|
>>>>Autres problèmes
et
exercices |