|
|
|||||||||||
|
|
|
|
|||||||||
|
|
TRAVAUX partie 1 |
|
|||||||||
|
|
|
|
|||||||||
|
|
1°) Résoudre l’inéquation suivante : 4 x + 3
> - 2 x + 5 donner les trois formes
d’expression du résultat. Sur 3 points |
|
|||||||||
|
|
2°) Résoudre l’équation
suivante : |
|
|||||||||
|
|
a) 4 x² - 11 x + 6 = 0 |
|
|||||||||
|
|
b) 5
x² - 11 x - 6 = 0 |
|
|||||||||
|
|
Sur 3 points |
|
|||||||||
|
|
TRAVAUX :
partie 2 |
|
|||||||||
|
Sur 14 points. |
|||||||||||
|
|
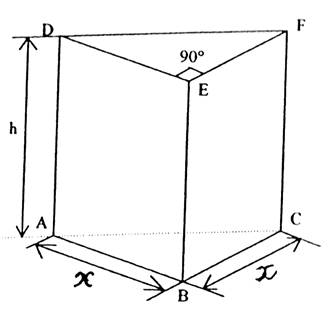
Soit le prisme droit ABCDEF représenté
ci contre en perspective. |
|
|
||||||||
|
|
1.1) Quelle est la nature de la
base ? |
|
|||||||||
|
|
1 .2) Quelle est la nature de
chacune des faces latérales : ABED ; ACFD ; BCFE ?. |
|
|||||||||
|
|
2.1 ) Calculer l’aire S de la base
ABC lorsque x = 4 cm |
|
|||||||||
|
|
2.2) Calculer le volume du prisme
lorsque x = 4 dm et h = 12 dm |
|
|||||||||
|
|
3.1) Le volume « V » de
ce prisme est donné par la relation : lorsque h = 4 dm , exprimer « V » en fonction
de « x » |
|
|||||||||
|
|
Cette formule est une fonction de
« x » : compléter l’égalité : |
|
|||||||||
|
|
f (x) = ……………… |
|
|||||||||
|
|
Puisque
f (x) = y ; et que V est y dans le repère ; compléter l’égalité : y (x) =
………………. |
|
|||||||||
|
|
On fait varier « x » de
0,5 à 3 dm Compléter le tableau des valeurs
ci- dessous avec V = 2 x² |
|
|||||||||
|
|
x |
|
0,5 |
|
|
2 |
2,5 |
3 |
|
||
|
x² |
|
|
|
2,25 |
|
|
|
||||
|
V |
0 |
|
2 |
|
|
|
|
||||
|
|
|
|
|||||||||
|
|
3.3 Dans un repère orthonormé,
représenter graphiquement la fonction « f » qui à « x »
associe « V » Echelle : abscisse : 4
unités représentent 1 dm ; ordonnée : 1 unité représente 1 dm3 |
|
|||||||||
|
|
Les grandeurs « x » et
« V » sont -elles proportionnelles ? justifier votre réponse. |
|
|||||||||
|
|
3.4 ) Quel est le nom de la courbe obtenue ? 3.5) Compléter le tableau ci
contre, en déterminant graphiquement les valeurs manquantes . |
|
|||||||||
|
|
|
|
x |
1,75 |
|
|
|
|
|
||
|
|
|
V |
|
10 |
|
|
|
||||
|
|
Laisser les lignes de construction apparente. |
|
|||||||||
|
|
4°) Calculer la hauteur du prisme
lorsque x = 6 cm et V = 144 dm3 |
|
|||||||||
|
|
5°) Calculer la valeur de
« x » lorsque h = 18 dm et V
= 29,16 dmE |
|
|||||||||
|
|
|
|
|||||||||