|
LOGICIEL warmaths
Pour Aide et Formation Individualisée
|
TRAVAUX
SOMMATIF NIV IV
|
Pour
aller directement aux informations « cours » voir cas
par cas.
|
|
INFORMATIONS
PEDAGOGIQUES :
|
|
DOSSIER N°
|
Matière : MATHEMATIQUES
|
Date :
|
|
|
|
|
TITRE : TRONC COMMUN
|
|
|
|
Classe :Bac
prof.
NIVEAU : niveau IV
|
CORRIGE.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N°
|
CONSIGNES
|
|
|
La séquence ne doit
pas dépasser 15 minutes (partie 1) +
45 minutes.(partie 2)
Matériel : le matériel habituel est autorisé :crayon , stylo, règle, rapporteur, compas,équerre, calculatrice.
Ecrire à l’encre, dessiner au crayon. (trait fin ,net
, précis.)
Le devoir est à rendre sur copie blanche.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TRAVAUX partie 1
|
|
|
|
|
|
|
|
1°) Résoudre l’inéquation suivante :
a)
4 x + 3 > - 2 x
+ 5
forme 1 par l’inéquation : x > 2 / 6 ;
forme 2 ; par l’intervalle : x = ] 1/3 ; + ¥ [
forme 3 par la représentation graphique : 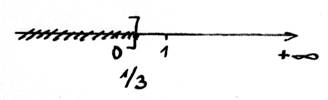
donner les trois formes d’expression
du résultat.
b) 3x - 5 > -5x + 13
; X > 2,25 ;
x = ] 2,25 ; + ¥ [
|
|
|
|
2°) Résoudre l’équation
suivante :
|
|
|
|
5 x² - 12 x + 9 = 0 ;
delta
négatif ; pas de solution.
|
|
|
|
4 x² - 11 x +
6 = 0 ; delta = 121
- 96 = 25 ; x’ = 0,75 ; x’’ = 2
|
|
|
|
5
x² - 11 x - 6 = 0 ; delta =
324 ; x ‘ = 0,6 et x’’ = - 3
|
|
|
|
|
|
|
|
TRAVAUX :
partie 2
|
|
|
|
|
|
Soit le prisme droit ABCDEF
représenté ci contre en perspective.
|
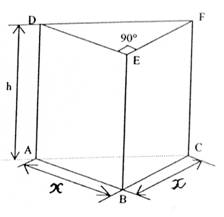
|
|
|
|
1.1)
Quelle est la nature de la base ? ABC un triangle rectangle isocèle (1/2 carré)
Le triangle ABC est un triangle « rectangle » en
B ;il est isocèle car AB = x et BC = x
|
|
|
|
1 .2) Quelle est la nature de
chacune des faces latérales :
ABED ; ACFD ; BCFE ?.les faces latérales sont des
rectangles, car c’est un prisme droit , que la base
est perpendiculaire aux faces et que ces faces sont parallèles.
|
|
|
|
2.1 ) Calculer l’aire S de la base ABC lorsque x = 4 cm
S = 8 dm²
|
|
|
|
2.2) Calculer le volume du prisme
lorsque x = 4 dm et h = 12 dm
V = 96 dm3 ou
96 000 cm3
|
|
|
|
3.1) Le volume « V » de ce
prisme est donné par la relation : 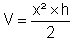
lorsque h = 4 dm ,
exprimer « V » en fonction de « x » : f(x) = 2 x²
|
|
|
|
On fait varier « x » de
0,5 à 3 dm
Compléter le tableau des valeurs
ci- dessous avec V 2 x²
|
|
|
|
x
|
0
|
0,5
|
1
|
1,5
|
2
|
2,5
|
3
|
|
|
x²
|
0
|
0,25
|
1
|
2,25
|
4
|
6,25
|
9
|
|
V
|
0
|
0,5
|
2
|
4,5
|
8
|
18,5
|
18
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3 Dans un repère orthonormé,
représenter graphiquement la fonction « f » qui à « x »
associe « V »
Echelle : abscisse : 4
unités représentent 1 dm ; ordonnée : 1 unité représente 1 dm3
|
|
|
|
Les grandeurs « x » et
« V » sont -elles proportionnelles ?
justifier votre réponse. Elles ne sont pas
proportionnelles pour 2 raisons : les points n’appartiennent pas à une
droite , et l’équation « 2x² » n’est pas de la forme « y = ax » qui est la forme de l’équation de la fonction
linéaire dont la représentation graphique est une droite.
|
|
|
|
3.4 ) Quel est le nombre de la courbe obtenue ?
3.5) Compléter le tableau ci
contre, en déterminant graphiquement les valeurs manquantes
.
|
|
|
|
|
|
x
|
1,75
|
2,24
|
|
|
|
|
|
|
|
V
|
6,1
|
10
|
|
|
|
|
|
Laisser les lignes de construction apparente.
|
|
|
|
4°) Calculer la hauteur du prisme
lorsque x = 6 cm et V = 144 dm3 :
h = 8 dm
|
|
|
|
|
|
|
|
|
|
|
|
|
|