Pré requis:
|
Tracés géométriques (angles) |
|
|
Les unités de longueurs |
ENVIRONNEMENT du dossier:
DOSSIER :
LE PERIMETRE « problèmes »
|
|
|
|
|
|
|
|
1
°) Donnez la définition de
"périmètre".
2°
) Quelle est l'unité usitée pour exprimer le résultat du calcul du périmètre ?
3°
)Donner la définition littérale relatif
au calcul du périmètre des figures géométriques suivantes:
|
Carré |
|
|
Rectangle |
|
|
Parallélogramme |
|
|
Trapèze |
|
|
Losange |
|
|
Triangle |
|
4°
) Donner la formule permettant de
calculer le périmètre des figures
géométriques suivantes:
|
Carré |
|
|
Rectangle |
|
|
Cercle |
|
5°
) Donner la formule permettant de calculer la longueur d' un arc
de cercle d'angle "alpha"
PROBLEMES
|
|
|
|
Calculer : 103,278901 km +347,0002 dam
+ 203455,03 mm + 45, 0000125 hm = ….m
=…..dm |
|
|
N°1 |
|
|
Problème
: on donne les mesures des cotés des champs d'un
plateau de table: a
= 1338 mm ; b = 34,5 cm ; c = 12,750
dm Calculer la longueur de placage nécessaire pour exécuter les
champs .
(utiliser le tableau de conversion ) |
|
|
N°2 :Construire un rectangle ABCD où la longueur AB mesure 5 cm et la largeur BC mesure 3 cm. Construire le cercle de diamètre [AC] |
|
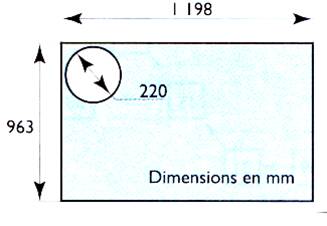
N°3
|
Une plaque à les dimensions suivantes . On veut plaquer les champs (coller une bande
sur les bords) Calculer la longueur minimale de plaquage qu’il faudra
prendre. (cercle exclu) |
|
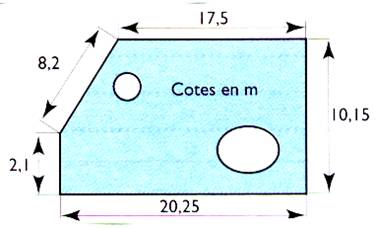
N°4
|
Calculer le périmètre de ce parterre de fleurs. |
|
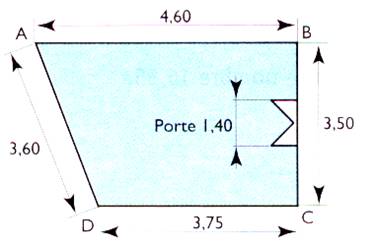
N°5 :
|
Calculer la longueur du périmètre de cette pièce
. |
|
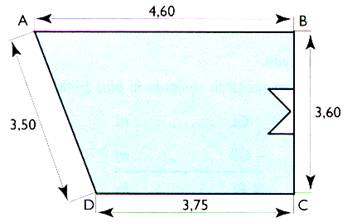
N°6
|
Calculer le périmètre de cette pièce . |
|
|
Sport : |
|
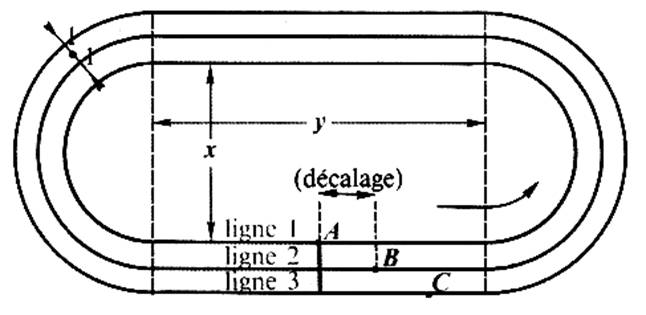
Ce problème est traité en arithmétique :
Les
tours de piste:
Une piste d'athlétisme possède 4 couloirs , un couloir par coureur.
Dans le dessin ci- dessus les couloirs ne sont pas
dessinés ,les lignes représentent le milieu
( l'axe) de chaque couloir.
1°) Exprimer en fonction de "x" et
"y" la longueur du tour de
piste 1.
2°) Exprimer en fonction de "x" et
"y" la longueur du tour de
piste 2.
3°) Exprimer en fonction de "x" et
"y" la longueur du tour de
piste 3.
|
|
|
|
4°) Si l'on veut
que le coureur "B"
ligne 2 , parcourt la même distance que le coureur "A"
ligne 1 , il faut un "décalage" entre les coureurs "A" et
"B" (voir figure)
Calculer ce décalage . Dépend- il de "x" ? ; de
"y" ?
5°) Montrer que le décalage entre les coureurs A et B et le même qu'entre les coureurs
"B" et "C" .