Module :		DOSSIER : 98 - 99
LOGICIEL warmaths; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
Info conseils et consignes.	TRAVAUX NORMATIFS Matière : MATHEMATIQUES. Niveau VI		.
PARTAGES INEGAUX ( LES PARTS sont INEGALES) 98 - Cas : Une des parts est multiple de l’autre. 99 - Cas :La somme et différence des parts sont connues
INFO COURS :
Info 1 @ « cours sur résoudre un problème du premier degré … » ; Info 2 @ « Suite des travaux sur la lecture de graphiques en lien avec les partages inégaux » ;
TRAVAUX CONTROLE
Doc WR
Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
TRAVAUX : EVALUATION
98 : Une part est multiple d’une autre Problème. Deux amies se partagent une caisse de 4,8 kg de poisson. L’une, dont la famille est nombreuse, en prend le triple de l’autre. Quel est la masse de chaque lot ? Ci dessous : la représentation graphique du partage : Le graphique montre que la caisse est partagée en 4 parts égales Une personne en prend une (1^er lot); l’autre en prend 3 (2^ème lot) : Une part pèse 4,8 kg : 4 = 1,2 kg; c’est le 1^er lot Le 2^ème lot est triple du 1^er 1,2 kg x 3 = 3,6 kg Vérifions ce que dit l’énoncé : 1°) le 2^ème lot est-il le triple du 1^er ? oui (3,6 kg = 1,2 kg fois 3) 2°) les 2 lots pèsent-ils ensemble 4,8 kg ? oui (1,2 + 3,6 = 4,8) Pour chaque problème de partage : 1°) traduisez l’énoncé par un graphique complet; 2 °) vérifiez vos réponses. CALCULS : 1. Un costume coûte 432 € . Le prix de la veste est le double du prix du pantalon. Quel est le prix de la veste ? le prix du pantalon? 2. Une oie et un poulet pèsent ensemble 6,5 kg. Le poids de l’oie est égal à 4 fois le poids du poulet. Combien pèse chacune des deux volailles ? 3. Un champ rectangulaire mesure 168 m de périmètre et sa longueur est triple de sa largeur. Quelles sont ses dimensions ? 4. Deux coupons d’étoffe valant 12,50 € le mètre mesurent ensemble 27 m. La longueur de l’un est double de celle de l’autre. Quelle est la valeur de chaque coupon? 5. Une maison vaut 5 fois le prix d’un champ; ensemble, ils valent 7 722 € . Voici la solution d’un élève, pour calculer la valeur du champ, puis de la maison: 7722 € :5 = 1544,4 € ; 7722 € —1544,4 € = 6177,6 € . Quelle est son erreur ? Quelle vérification devrait la révéler ? Écrivez la solution correcte. 6. Un cinéma compte 354 places : places de parterre à 2,8 € la place et places de balcon à 3,2 € . Le nombre des places de parterre est double du nombre des places de balcon. Quel est le montant de la recette quand toutes les places sont occupées? 7. Le produit de leur pêche est ainsi partagé entre les membres de l’équipage d’un bateau : le mousse a une part, chacun des deux matelots 2 parts, le patron 5 parts. Combien chacun a-t-il touché le jour où le bateau est rentré avec 820 kg de poisson qui fut vendu à 1,35 € le kg? 8. Caroline, Claire et Gabriel héritent de leur oncle une somme de 950,4 € . La part de Caroline est triple de celle de Claire qui est elle-même la moitié de celle de Gabriel. Quelle est la part de chacun ? 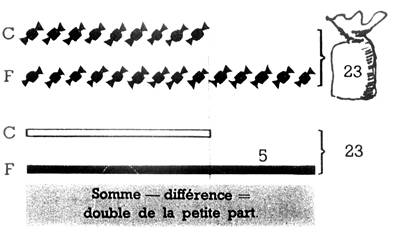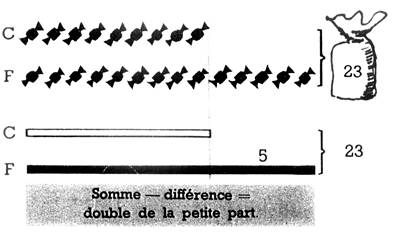99 - Somme et différence des parts est connues Problème. Julien et Francine partagent 23 caramels, et Francine en reçoit 5 de plus que Julien . Quelle est la part de chacun ? Graphique n°1: il montre que : Somme - différence = le double de la petite part . la part de Julien (23 — 5 ) 2 = 9 ; la part de Francine 9 + 5 = 14 Vérification 9 + 14 = 23 Graphique n°2 , il montre que : Somme + différence = le double de la grande part . la part de Julien (23 — 5 ) 2 = 9 ; la part de Francine 9 + 5 = 14 Vérification 9 + 14 = 23 SITUATIONS PROBLEMES : 1. Papa et Maman ont ensemble 57 ans. Maman a 5 ans de moins que Papa. Quel est leur âge? Comment se posera ce problème dans 8 ans ? 2. Calculez deux nombres dont la somme est 120, la différence 36. Vérifiez votre réponse en partageant un segment de 120 mm en 2 segments dont l’un mesurera 36 mm de plus que l’autre. 3. Dessinez autant que vous voulez de rectangles différents ayant pour côtés un nombre entier de cm, et 16 cm de périmètre. Quel est celui qui a une longueur dépassant la largeur de 4 cm ? Y en a-t-il d’autres ? 4. On demande de partager 240 € entre Annie et Sylvie, de façon que Sylvie ait 30 € de moins qu’Annie. Voici les réponses de trois élèves 1° Annie 150 € 2° Annie 150 € 3° Annie 135.€ Sylvie 120 € Sylvie 90 € Sylvie 105 € Quelles vérifications prouvent que deux solutions sont fausses ? Où est la bonne ? Comment l’élève a-t-il compté ? 5. L’épicier a acheté pour 35,70 € deux caisses de pommes dont l’une pèse 6 kg de plus que l’autre. Les pommes valant 85 c le kg, calculez la masse , puis le prix de chaque cageot. 6. il a fallu 632 m de fil de fer pour entourer d’un double rang un terrain rectangulaire dont la longueur dépasse la largeur de 29 m . Quelles sont les dimensions du terrain? 7. Marine et Michelle ont ensemble 84 € . Si Marine donne 8 € à Michelle, elles auront autant l’une que l’autre. Combien chacune a-t-elle? 8. Deux péniches livrent ensemble 382 t de charbon à une usine à gaz. Quand on a déchargé 29 t de l’une et 48 t de l’autre, elles contiennent la même masse de charbon. Quelles questions posez-vous ? Répondez-y. 9. Un terrain à bâtir de 845 m² est partagé en deux parcelles inégales, dont l’une mesure 75 m ² de plus que l’autre, a) Quelle est la surface de chaque parcelle ? b) La différence de prix des deux parcelles est 1 350 € . Quelle est la valeur de chaque parcelle?