Module :		DOSSIER :
LOGICIEL warmaths ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
Info conseils et consignes.	TRAVAUX SOMMATIFS PRIMAIRE / COLLEGE /LYCEE Matière : CALCULS et PROBLEMES		@Info cours.
Mouvements uniformes et vie courante.
INFO COURS :
TRAVAUX CONTROLE
Doc WR
Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours . Savoir refaire le tableau
TRAVAUX : EVALUATION
Mouvements uniformes N°1 : A ) Représentons sur un papier quadrillé, de préférence millimétré, le mouvement d’un cycliste qui roule à 20 km/h en hauteur, indiquons les distances; en largeur, le temps qui s’écoule; chaque point A, B, C représente la position du cycliste, par rapport au point de départ, au bout d’une heure, de 2, de 3 heures... On pourrait aussi chercher des positions intermédiaires. Une ligne qui joint les points A, B, C, représente toutes les positions du cycliste pendant la durée de son déplacement on y lit par exemple que le point D représente sa position après i h 30 mn de route, à 30 km du départ.
B ) Sur le graphique ci-contre , lire à quelles durées du mouvement, et à quelles distances parcourues correspondent les points E, F, G.
C) Cherchez, sur la ligne des durées du graphique ci-contre, les points qui correspondent à une durée de1 h 15 mn; 2 h 45 mn; 0h 15 mn. En suivant les lignes du quadrillage, trouvez les points de la ligne du mouvement qui leur correspondent, et, partant de ces points, trouvez les distances correspondantes auxquelles se trouve le cycliste à ces moments-là.
D) a) Quelle durée représente 1 mm, sur le graphique ci-dessus? b) Quelle distance représente 1 mm ? Sans calculs, par lecture du graphique, dites : c) à quelle distance du point de départ se trouvait le cycliste après 2 h 15 mn de route; d) après 2 h 39 mn; e) au bout de combien de temps le cycliste se trouvait à 16 km du point de départ; à 44 km.
Problème N°2 : La ligne « VM » du graphique ci-contre représente la marche d’un vélomoteur, la ligne C celle d’un cycliste, qui ont 60 km à parcourir sur la même route. a) A quelle heure part chacun d’ eux?. b) Quelle distance parcourt le vélo- moteur pendant la 1^ère heure? c) Il s’arrête au 40^e km. A quelle heure repart-il? A quelle heure arrive-t-il au bout du trajet? d) A quelle vitesse roule le cycliste? A quelle heure arrive-t-il au but de son voyage? Combien de temps après le vélomoteur?
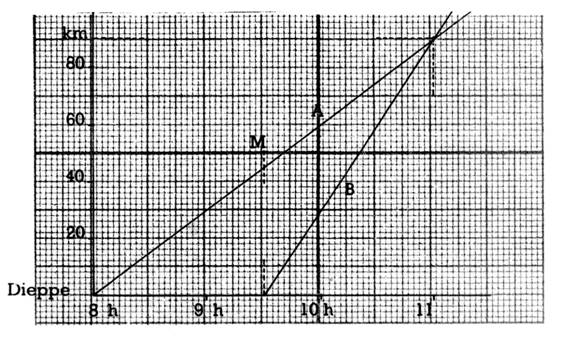
3 Le graphique ci-contre représente le déplacement d’un cycliste (A) et celui d’un motocycliste (B) s’éloignant tous deux de Dieppe, sur la même route. Dites pour chacun a) son heure de départ; b) sa vitesse par heure. c) Quand part le motocycliste, le cycliste est en M quelle est son avance sur le motocycliste (en km)? (Vérifiez par le calcul.) d) A quelle heure le cycliste est-il rejoint? A quelle distance de Dieppe?
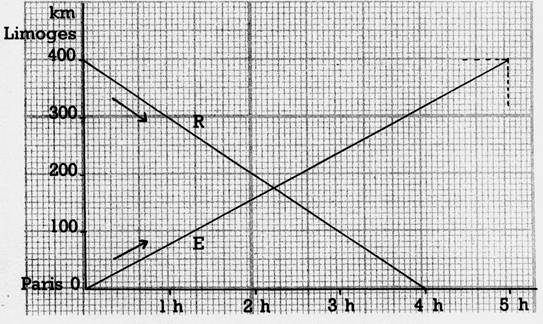
4°) Le graphique ci-dessous représente la marche de 2 trains un rapide R, qui va de Limoges à Paris, un express E qui va de Paris à Limoges, et qui partent en même temps. a) Quelle est la vitesse de chacun? Le calcul, en examinant les distances et les heures d’arrivée, vous donne-t-il le même résultat que l’examen du graphique? b) Au bout de combien de temps se croisent-ils-? Et à quelle distance de Paris? A quelle distance de Limoges? c) A quelle distance de Paris se trouve l’express quand le rapide arrive à Paris? (Vérifiez par le calcul.)
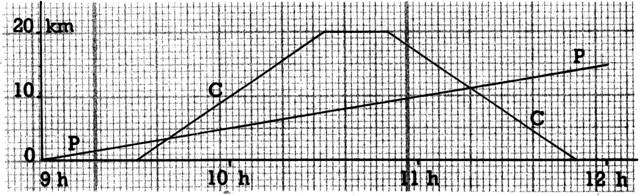
5 ° ) Le dessin ci-contre représente le déplacement de 2 mobiles partis du même village, dans la même direction, mais à des heures différentes . 1°) un piéton (P) qui va voir un parent à 15 km de là, et qui marche régulièrement, sans s’arrêter; 2°) un cycliste (C) qui, roulant régulièrement, va à la ville voisine, y reste 20 mn, et revient à la même allure. a) Quelles sont les heures de départ? b) Quelle est la vitesse de chacun? c) Quand, comment et à quelles distances du village de départ le cycliste rencontre-t-il le piéton ?