|
>>>> Corrigé |
|
|
||
|
Fin 3ème de collège |
CORRIGE TRACES DE TRIANGLES ( en PRE REQUIS à Pythagore) Matériel : règle graduée , compas , équerre ,
rapporteur……. |
|
||
|
Résolutions de
triangles par le tracé Ces tracés permettent
de « résoudre » des triangles rectangles NOTA : Ces tracés
sont à conserver , Ils seront repris
pour étudier :PYTHAGORE et sa réciproque. Dans tous les cas il
faut rendre compte. (après avoir fait
le tracé sur feuille ) : Vous devez donner pour
chaque triangle : les 3 mesures
de longueurs et les 3 mesures d’angles qui caractérisent un triangle. Travaux
à débuter en classe , à terminer chez soit . A rendre sur feuille pour
le …………………………. |
|
|||
|
Série 1 : |
|||||
|
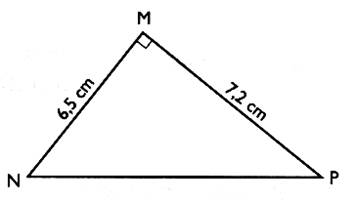
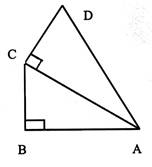
1°) Soit un triangle
rectangle NMP , rectangle en M . Tracer le triangle ( échelle 1) , et mesurer « NP » . Avec un
rapporteur donner la mesure des 3 angles : Calcul de la somme des trois angles : |
|
||||
|
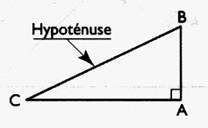
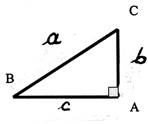
2°) Tracer le triangle BAC dont les côtés
mesurent respectivement : 30 ; 40 ; 50 mm ; est - il rectangle ? C’est un triangle rectangle ; il
possède un angle droit ( 90°) |
|||||
|
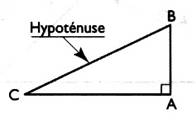
3° ) Tracer le triangle BAC dont les côtés
mesurent respectivement : 15 ; 20 ; 30
mm ; est - il ? . Ce n’est pas un triangle rectangle ; c’est un triangle
quelconque dit « scalène » |
|||||
|
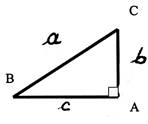
4°) Tracer le triangle ( échelle 1 = 1cm) , Donner la valeur des mesures manquantes. (angles et
longueurs) On donne : AC = 4
; AB = 3 ; CB = 5 |
|
||||
|
5°) On donne : BC = 20 mm ; AC = 16 mm; Tracer le triangle ( échelle 2) , Donner la valeur des mesures manquantes. (angles et
longueurs) |
|
||||
|
6°) On donne : BC = 42 mm ; AB = 21 mm; Tracer le triangle ( échelle 2) , Donner la valeur des mesures manquantes. (angles et
longueurs) |
|
||||||
|
Pour chaque cas : Tracer le triangle rectangle et compléter le tableau |
|||||||
|
|
|
Triangle
1 |
Triangle
2 |
Triangle
3 |
Triangle
4 |
Triangle
5 |
|
|
a |
|
37
cm |
|
0,65
m |
295
mm |
||
|
b |
450
mm |
35
cm |
45
cm |
|
2,36
dm |
||
|
c |
600
mm |
|
280
mm |
0,33
m |
|
||
|
|
|
|
|
|
|
||
|
Série III |
||||
|
Tracer le triangle rectangle et compléter le tableau |
||||
|
N°1 |
|
Données : |
Ici les
6 Réponses : |
|
|
BA = 108 mm |
|
|||
|
CA = 45 mm |
||||
|
|
||||
|
|
||||
|
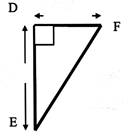
N°2 |
Tracer le triangle rectangle et compléter le tableau |
Données : |
Ici les
6 Réponses : |
|
|
|
|
DF = 127
mm |
|
|
|
DE = 156
mm |
|
|||
|
|
|
|||
|
|
|
|||
|
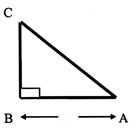
N°3 |
Tracer le triangle rectangle et compléter le tableau |
Données : |
Ici les
6 Réponses : |
|
|
|
|
CA = 74 cm |
|
|
|
CB = 24 cm |
|
|||
|
Calculer
AB. |
|
|||
|
|
|
|||
|
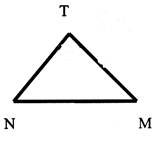
4°) |
Tracer le triangle et compléter le tableau. |
Données : |
Ici les
6 Réponses : |
|
|
|
|
NM = 13,75
cm |
|
|
|
NT = 11 cm |
|
|||
|
Calculer
TM |
|
|||
|
Est -il rectangle ? |
|
|||
|
N°5 |
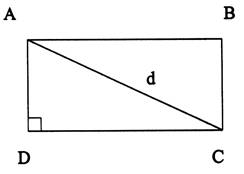
Tracer le rectangle et compléter le tableau Comment appelle - t on « d » dans le rectangle |
Données : |
Ici les
6 Réponses : |
|
|
|
AB = 170 cm |
|
|
BC = 95 cm |
|||
|
|
|||
|
« d » = ? Donner les valeurs des angles (précisez pour quel triangle ) |
|
N°6 |
Tracer le triangle et compléter le tableau |
Données : |
Ici les
6 Réponses :: |
|
|
|
CB = 114
cm |
|
|
HB = 71 cm |
|||
|
« h »
= 83 cm |
|||
|
AB = ? AC = ? Donner les valeurs des angles (précisez pour quel triangle ) |
|||
|
N°7 |
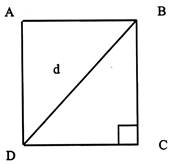
Tracer le carré
et « d » |
Données : |
Ici les
6 Réponses : |
|
|
|
BC = 32 dm |
: |
|
Quel nom donne t- on à « d » ? En déduire
la valeur de AB ; CD ; AD. Donner les valeurs des angles (précisez pour quel triangle ) |
|
|
|
|
|
||
|
N°8 |
Tracer Le
triangle rectangle suivant |
Données : |
Ici les
6 Réponses : |
||
|
|
|
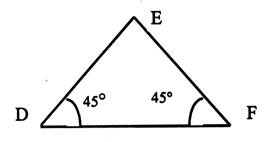
-Calculer l’angle E : -Quelle est la nature du triangle ? -DE = 16 cm En déduire
EF Calculer DF |
|
||
|
|
|||||
|
8 b ++ |
Trouver « DE » si « DF » est égal à 6 cm
|
|
|
||
|
8c |
|
Données : |
Ici les
6 Réponses : |
||
|
|
|
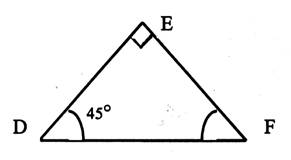
Calculer l’angle F : -Quelle est la nature du triangle ? -DE =
5 cm En déduire
EF Calculer DF |
|
||
|
|
|
|
|
||
|
N°9 |
Tracer la figure suivante : |
Données : |
Ici les
6 Réponses : |
||
|
|
|
Sachant que DC = 31 m |
|
||
|
CB = 33 m
et BA= 56 m |
|||||
|
AC
= ? |
|||||
|
Donner les valeurs des angles (précisez pour quel triangle ) |
|||||
|
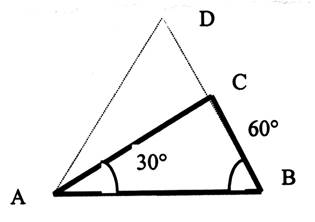
N° 10 a |
Tracer le triangle |
Données : |
Ici les
6 Réponses : |
|
|
|
|
En déduire l’angle C |
|
|
|
Que peut -on dire du triangle ACB , au regard du
triangle ADB ? |
||||
|
Quelles sont les valeurs des angles : A CB = D C A = C D A = CAD = La longueur de : AB = 100
mm En déduire
CB Mesure
AC (au mm
prés) |
||||
|
|
|
|||
|
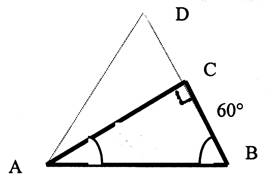
N°10 c |
Tracer le triangle ci dessous |
Données : |
Ici les
6 Réponses : |
|
|
|
|
En déduire l’angle C |
|
|
|
Que peut -on dire du triangle ACB , au regard du
triangle ADB ? |
||||
APPLIQUATION : PRISME DROIT ( corrigé)
|
N° |
Figure |
Données : |
|
|
|
|
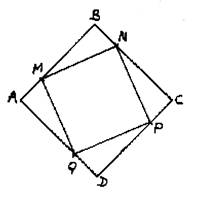
Soit le carré
ABCD. On sait que : AB= 60 mm AM = BN = CP = DQ = 15 mm On demande : 1°) mesurer
les dimensions du carré MNPQ. |
|
|
N° |
Figure |
Données : |
|
|
|
|
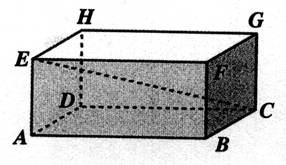
ADCB est la base du prisme.. Les dimensions du parallélépipède
rectangle sont : (en mm) L = 120
mm ; Largeur = 40 mm Hauteur = 30 mm Mesurer les
dimensions EB = BG = EC = |
|
|
N° |
Figure |
Données : |
|
|
|
|
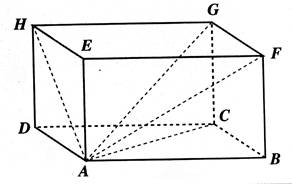
DCBA est
la base du prisme.. Les dimensions du parallélépipède rectangle sont : (en
mm) L = 100 mm ;
Largeur = 40 mm Hauteur = 40 mm Faire un plan vue par vue et Mesurer la longueur : HA = GA = FA = CA = |
|
|
N° 14 |
Parallélépipède rectangle . |
Données : |
|
|
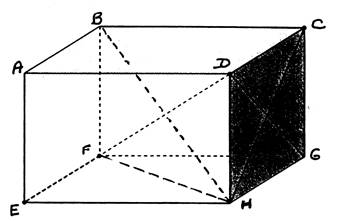
Les dimensions du prisme droit sont : 6 cm
X 4 cm X 3 cm la vue de face mesure 6 cm par 3 cm. 1°) Tracer
le prisme en perspective cavalière. 2°) Tracer les vues et mesurer les dimensions réelles de
: ED = FH = HC = En plus : 3°) calculer la surface latérale du prisme. 4°) calculer la surface totale du prisme. 5°) Calculer le volume du prisme. 6°) Calculer la masse du prisme ( masse volumique = 1,2 kg / dm3 7°) Calculer le poids du prisme. |
|