Pré requis:
|
Soustraction de deux nombres relatifs |
|
BIPOINT
|
ENVIRONNEMENT du dossier:
|
Tableau |
DOSSIER PROJECTION d ' un point dans un repère
cartésien (deux droites sécantes)
|
TEST |
COURS |
Interdisciplinarité |
|
Voir définition du mot « direction et sens ».
Mots
utilisés dans l’objectif : le vecteur
Préambule :
La
projection d ’ un point ; d’un segment (un ensemble de points alignés)
implique que l’on doit connaître (ou se
fixer) :
n
une direction
(c’est une droite )
n
la position du point dans
un plan ( en l’occurrence la feuille)
et
n
la droite support qui recevra le
« projeté du point » .
Rappel :
Projection d’un segment de droite:
« x » :
Avec
A et B on construit le segment AB;
Le segment
Ax Bx est le projeté du
segment AB sur la droite
« axe » ,par rapport à la droite d .
XA
est l’abcisse du point A;
XB est l’abcisse du point B
![]()
 B
B
A
d
![]()
A’ B’ x
Projection d’un segment sur un
repère (cas général)
|
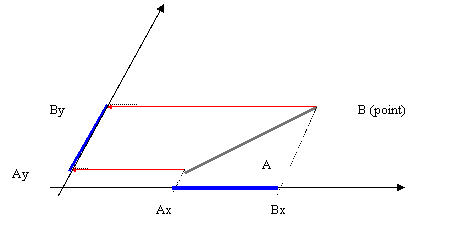
Avec A et B on construit le segment AB . Sur l' axe "x" et sur l ' axe
"y" : By
est le projeté de B sur l’axe
« y ». Ay est le projeté de A sur l’axe
« y ». Y A
est l’ordonné du point A Y B
est l’ordonné du point B |
Les segments de droites [Ay By]
et [B x A x] sont
appelés les projetés du
segment AB . La norme
permet de graduer les axes. Si la
norme * sur x et
y est égale
« mesure » le repère est dit « normé » *Voir la signification de [O,I] et [ O, J ] |
II)
Projection d’un segment sur
deux droites sécantes perpendiculaire :
(appelé aussi repère
cartésien orthogonal - normé (cliquer ici pour
en savoir plus
)»
Objectif
important pour :.représentation graphique des ...FL et F affine ; les relations
trigonométriques; vecteurs et ses
composantes ;……. )
![]() y
y
![]() Ay
A
Ay
A
![]()
![]()
![]()
![]()
![]()
![]() By B
By B
Bx
Ax x
|
GEOMETRIE DANS L’ESPACE Voir projection d’un point ,d’un segment ,d’une surface , d’un volume
dans un repère en trois dimensions
(dit dans l’espace ) |
|
A ) Montrer par un dessin ,la projection orthogonale d’un point .
D D1 delta M
![]()
![]()
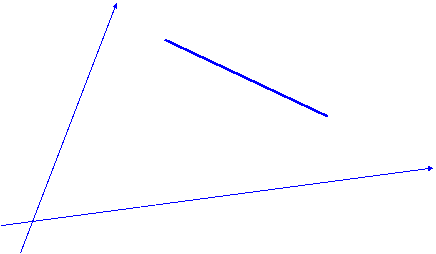
 I ) Soit le schéma suivant ,tracez le projeté du point M par
rapport à « delta » sur la
droite D et la droite D1.
I ) Soit le schéma suivant ,tracez le projeté du point M par
rapport à « delta » sur la
droite D et la droite D1.
II )
Soit un repère non orthogonal : tracer
les projetées du segment
B
III ) Soit un repère
orthonormé ( à compléter):
tracer les projections du segment
AB ; donner les coordonnées des deux points,
![]()
![]()
![]()
![]() échelle1
échelle1

![]()
Cet exercice sera repris avec Obj :
« Pythagore »
en vue de rechercher la norme d’un vecteur par le calcul
Le vecteur Vx et le
vecteur Vy sont les composantes du
vecteur V. Ces composantes ont pour origine ,l’origine du vecteur V ,pour direction , les parallèles aux droites d et d ’ et pour extrémité des parallèles aux droites d et d ’ passant par l’extrémité du vecteur V I
Composantes d’un vecteur:
![]()
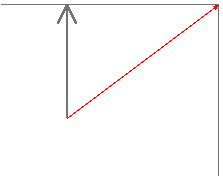
![]()
![]() d’
d’
Vy V
![]()
Vx
![]()
d
Projection des composantes d’un vecteur:
Le vecteur
Vx et le vecteur Vy sont
les projections du vecteur V Nous avons
dessiné le cas ou les
projection sont orthogonales , parce que les axes x et y sont orthogonaux
![]() y
y
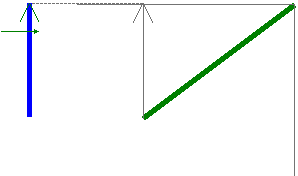
![]() Vy
Vy
V

![]()
![]() x
x
Vx
CALCUL DES
COMPOSANTES D’UN VECTEUR:
![]()
![]()
![]() V ,
Vx et Vy
forme un triangle
« rectangle » si le
repère est orthonormé
V ,
Vx et Vy
forme un triangle
« rectangle » si le
repère est orthonormé
A partir des coordonnées de
l’origine est l’extrémité du vecteur ,on peut donc calculer toutes les
caractéristiques du triangle.
Pour trouver les
caractéristiques du triangle rectangle on fait appel : à
« Pythagore » ou
aux relations trigonométriques dans le triangle rectangle (sinus, cosinus, tangente ,cotangente)
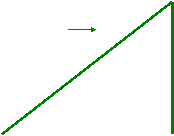
![]() V
V
V y
![]()
![]()
Vx