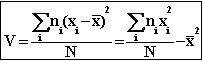INFORMATIONS :
|
|
Niveau IV : STATISTIQUES |
DEVOIRS de CONTROLE :
Q1 ) 1°) La statistique est l'étude des données relatives à un groupe d'individus.
I.
VOCABULAIRE, DEFINITIONS
¶ Population : la population est
l'ensemble des unités statistiques(ou individus) sur
lequel vont porter les observations
· Echantillon : c'est une partie
de la population.
¸ Caractère : Un caractère statistique est une propriété étudiée de la
population.
Un
caractère peut-être :
v
Quantitatif : si
on peut lui attribuer une valeur numérique.
v
Qualitatif : s'il n'est pas
représenté par un nombre
v
Discret : s'il ne prend que
certaines valeurs
v
Continu : s'il peut prendre
toutes les valeurs dans un intervalle donné.
Evaluation N°1
Dans
un magasin de chaussures on a relevé durant une semaine les pointures des
chaussures vendues dans celui-ci :
38 38 39 42 43 43 41 44 41 37 36 35 41 42 45 38 43 42 41 42 38 37 39 40 36 35 40 35 37 40 41 36 37 36 39 45 36 36 38 39 37 39 42 44 42 39 37 43
37 41 40 40 38 36 37 41 42 38 39 41
Dans
cet exemple :
Quelle
est la population ? la
population est "l'ensemble de chaussures"
Quel
est le caractère ? Le caractère étudié est la pointure
Est-il : qualitatif ou quantitatif ; est-il
discret ou continu ?
il est quantitatif et discret.
¹ Classe : Une classe est un sous-ensemble de la
population correspondant à des valeurs du caractère comprises dans un
intervalle [a ; b[.
Comment
calcule - t -on l’amplitude d’une classe [a ; b[?
L'amplitude d'une classe [a ; b[ est la
différence entre ses deux bornes : b-a
Donner
la formule permettant de calculer le centre d’une classe :
Le centre de la classe est : ![]()
º Effectif : L'effectif d'une
classe ou d'une valeur est le nombre d'éléments qui correspondent à cette
classe ou à cette valeur.
Comment
le note - t-
on ? On le
note en général ni.
Evaluation
N°2
Dans
l'exemple n°1, on peut regrouper les pointures par classe d'amplitude 2 dans un
tableau statistique :
|
Valeurs de la pointure |
Effectif( à compléter ) |
|
[ 35 ; 37 [ |
n1 = ….. |
|
[ 37 ; 39 [ |
n2 = …… |
|
[ 39 ; 41 [ |
n3 =…... |
|
[ 41 ; 43 [ |
n4 =…... |
|
[ 43 ; 45 ] |
n5 =…... |
|
|
N = n1 + n2
+ n3 + n4 +n5 = 60 |
» Fréquence
Définition : On appelle
fréquence fi d'une propriété d'un caractère le rapport de l'effectif ni de cette propriété par
l'effectif total N.
Traduire sous forme d’une formule : la formule est ![]()
Combien
vaut la somme des fréquences ?: ( la somme des fréquences fi vaut 1)
Ces
différentes fréquences peuvent être exprimées
sous forme de pourcentage.
Donner
la formule qui permet d’exprimer en pourcentage les fréquences :
![]()
Combien vaut en pourcentage la somme des fréquences ?
la somme des fréquences fi
vaut 100 %
Evaluation
n°3 :
on donne la formule ![]()
Calculer
les fréquences de chaque classe dans l ‘ évaluation 1
|
Valeurs de la pointure |
Fréquence(en %)( à compléter ) |
|
[ 35 ; 37 [ |
f1 = ….. |
|
[ 37 ; 39 [ |
f2 = …… |
|
[ 39 ; 41 [ |
f3 =…... |
|
[ 41 ; 43 [ |
f4 =…... |
|
[ 43 ; 45 ] |
f5 =…... |
¼ Effectifs et fréquences cumulés
A
quoi est égal l'effectif cumulé croissant (ECC ) (ou la fréquence cumulée croissante (FCC) de
la valeur de rang « i » ?
l'effectif cumulé croissant
(ECC ) (ou la fréquence cumulée
croissante (FCC) de la valeur de rang « i » est égal à la somme de tous les effectifs (de
toutes les fréquences) jusqu'au rang « i » compris.
A
quoi est égal l'effectif cumulé décroissant (la fréquence cumulée décroissante) de
la valeur de rang « i » ?
l'effectif cumulé
décroissant (la fréquence cumulée
décroissante) de la valeur de rang « i » est égal à la somme de tous les effectifs (de toutes les
fréquences) à partir de la dernière valeur jusqu'au rang i compris.
Evaluation n°4 :
Voici
regroupés les salaires de 85 employés d'une entreprise, remplir les deux
dernières colonnes.
|
Montant ( €) |
Nombre de
salariés |
Effectif cumulé croissant (ECC) |
Effectif cumulé décroissant (ECD) |
|
[ 0 ; 200 [ |
9 |
9 |
85 |
|
[ 200 ; 400 [ |
28 |
37 |
76 |
|
[ 400 ; 600 [ |
25 |
62 |
48 |
|
[ 600 ; 800 [ |
16 |
78 |
23 |
|
[ 800 ; 1 000 [ |
7 |
85 |
7 |
|
Total |
85 |
|
|
Voici
la même situation mais , remplir le tableau suivant
,avec les fréquences cumulées croissantes et décroissantes
|
Montant en € |
Nombres de salariés. |
Fréquences |
Fréquence cumulée croissante. (FCC) |
Fréquence cumulée décroissante. (FCD) |
|
[ 0 ; 200 [ |
9 |
0,106 |
0,106 |
1 |
|
[ 200 ; 400 [ |
28 |
0, 329 |
0,435 |
0,894 |
|
[ 400 ; 600 [ |
25 |
0, 294 |
0,729 |
0,
565 |
|
[ 600 ; 800 [ |
16 |
0, 188 |
0, 917 |
0,271 |
|
[ 800 ; 1000 [ |
7 |
0,083 |
1 |
0,083 |
|
Total : |
85 |
1 |
|
|
Evaluation
n°5
Lors
d'une élection présidentielle on a relevé le nombres de voix
obtenus par les cinq candidats au premier tour :
|
Candidats n°1 |
Candidat n°2 |
Candidat n°3 |
Candidat n°4 |
Candidat n°5 |
|
2 555 832 |
1 200 132 |
3 132 450 |
1 458 325 |
2 128 441 |
Nombre total de votants :
1°) Quel est le caractère
étudié ?
2°) Calculer la fréquence f1
en % des votes pour le candidat
n°1
3°) Calculer la fréquence f2 en % des votes pour le candidat n°2
4°) Calculer la fréquence f3 en % des votes pour le candidat n°3
5°) Calculer la fréquence f4 en % des votes pour le candidat n°4
6°) Calculer la fréquence f5 en % des votes pour le candidat n°5
7°) Y-a
t-il un candidat élu au premier tour ?
(Arrondir
les résultats au dixième.)
II. REPRESENTATIONS GRAPHIQUES
II.1. GRAPHIQUES DES
EFFECTIFS ET FREQUENCES
¶ Le diagramme
circulaire (ou à secteurs)
Il est souvent utilisé pour représenter des séries
statistiques à caractère qualitatif.
A quoi est égale l’aire du secteur circulaire ?
L'aire du secteur angulaire est
proportionnelle à l'effectif ou à la fréquence.
La valeur de
l'angle (en degré) correspondant à l'effectif ni se calcule à l'aide
de la formule (N est l'effectif total) : ![]() , à partir de la fréquence fi ( en % ) la
formule devient :
, à partir de la fréquence fi ( en % ) la
formule devient : ![]() .
.
|
Couleur des yeux |
Nombre de personnes |
Calcul de
l'angle en degré |
|
Marron |
788 |
|
|
Bleu |
300 |
|
|
Vert |
225 |
|
|
Gris |
577 |
|
|
|
Total : 1890 |
360 |
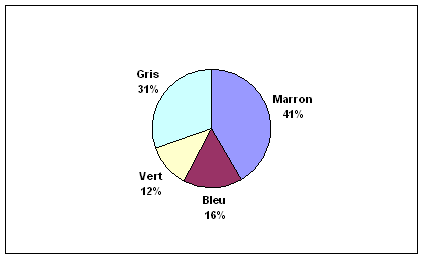
EVALUATION N°6: Dans le tableau
statistique suivant on a regroupé le nombre de personnes en fonction de la
couleur de leurs yeux sur un échantillon de 1890
Compléter ce tableau et représenter ces résultats
par un diagramme circulaire.
|
|
|
Construire le diagramme circulaire :
|
|
· Le diagramme à bâtons
Que peut -on représenter avec un diagramme à bâtons ?: On peut représenter
des effectifs ou des fréquences d'une variable discrète à l'aide de ce
diagramme.
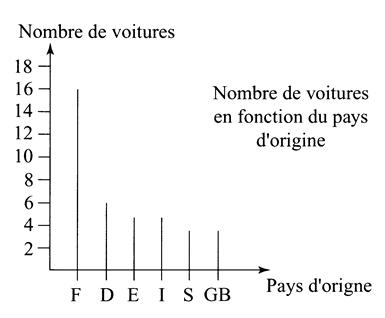
EVALUATION N°7
On étudie la répartition de voitures en fonction du pays d'origine :
|
Pays |
F |
D |
E |
I |
S |
GB |
|
Effectifs |
17 |
6 |
4 |
4 |
3 |
3 |
Construire le diagramme à bâtons.
|
solution |
|
¸ L'histogramme
Compléter les phrases :
On représente à l'aide de ce graphique des séries à variable continue.
Un histogramme des effectifs (ou fréquences) est constitué
de rectangles ayant pour base l'amplitude des classes
et dont les aires sont proportionnelles aux
effectifs ( ou fréquences).
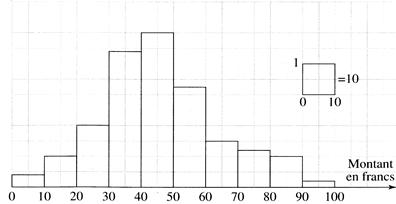
EVALUATION N°8 :
v
Dans le cas de classes de
même amplitude : construire le diagramme.
|
|
v
Dans le cas de classes
d'amplitude différentes : Que peut -on dire sur la
représentation de l’effectif (compléter la phrase)
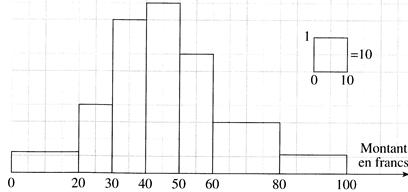
|
Montant en Francs |
Effectifs |
Hauteur |
|
[
0 ; 20 [ |
14 |
0,7 |
|
[
20 ; 30 [ |
20 |
|
|
[
30 ; 40 [ |
44 |
4,4 |
|
[
40 ; 50 [ |
50 |
5 |
|
[
50; 60 [ |
32 |
3,2 |
|
[
60 ; 80[ |
28 |
1,4 |
|
[
80 ; 100[ |
12 |
0,6 |
Dans ce cas,
l'effectif est représenté par la valeur de la surface
du rectangle qui dépend des unités graphiques choisies.
II.2. Polygone des effectifs cumulés et des
fréquences cumulées
Par quoi est formé le polygone des E.C. ou des F.C. (donner des
précisions sur le choix des abscisses et ordonnées des points) ?
Il
est formé des segments de droites joignant les points :
-
d'abscisses, la
borne supérieure d'une classe.
-
d'ordonnées :
l'effectif cumulé de cette classe.
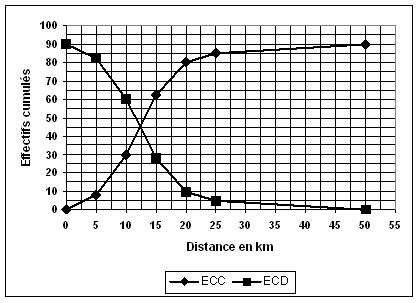
EVALUATION N°9
Dans le tableau suivant, on a regroupé par classe
d'amplitude 5 (sauf pour la dernière dont amplitude 25 )
les distances séparant le lycée de l'entreprise pour 90 élèves en stage.)
|
Distance en km |
Nombre d'entreprises |
ECC |
ECD |
|
[0 ; 5 [ |
8 |
8 |
90 |
|
[ 5 ; 10 [ |
22 |
30 |
82 |
|
[ 10 ; 15 [ |
32 |
62 |
60 |
|
[ 15 ; 20 [ |
18 |
80 |
28 |
|
[ 20 ; 25 [ |
5 |
85 |
10 |
|
[ 25 ; 50 [ |
5 |
90 |
5 |
|
[Total |
90 |
|
|
Construire
les deux polygones
.
Pour les deux graphiques, le premier point a pour
coordonnées ( 0 ; 0 ) pour l'ECC
et ( 0 ; 90) pour l'ECD.
|
|
III. CARACTERISTIQUES DE POSITION
III.1. MODE, CLASSE
MODALE
Qu’appelle - t
- on « mode » ?
Le mode est la valeur de la variable qui correspond à l'effectif ou à la
fréquence maximale.
Qu’appelle -
t- on « classe modale » ?
Dans le cas de série à variable continue,
on parle de classe modale ( les classes ayant même
amplitude).
Evaluation N° 10 :
Dans l'exemple précédent ,
quelle est la classe modale ?
la
classe modale est [ 10 ; 15 ]
III.2. MOYENNE ARITHMETIQUE
Dans la formule ci - dessous que désigne les
« xi » et les
« ni » ? :
Les
x1, x2….,xp sont les valeurs du caractère étudié et
les n1, n2,….., np les effectifs
|
Que permet de calculer la formule ci -
contre ? la moyenne arithmétique |
|
où
N est l'effectif total. |
Avec les fréquences, la formule devient :
|
Que permet de calculer la formule ci -
contre ? la moyenne arithmétique |
|
|
REMARQUE:
Compléter la phrase : Pour les séries statistiques
continues, « xi » représente la valeur
du centre de la classe.
III.3. MEDIANE
La médiane est la valeur de la
variable qui partage l'effectif total en deux parties de même effectif
Pour un caractère discret :
Si l'effectif total est impair, la médiane est la valeur du caractère situé au milieu de la série
Si
l'effectif est pair la médiane est la demi somme des
deux valeurs centrales du caractère.
Pour un caractère continu :
La médiane peut être recherchée par lecture sur le
graphique de la courbe des effectifs cumulés, de l'abscisse
correspondant à l'ordonnée N/2
Evaluation N° 10 :
Dans l’ Evaluation N° 9 , le caractère
étudié est continu ( nombre de km), quelle est la valeur de la
médiane : 12,5.Elle
correspond au point dont l'ordonnée est de
90/2 = 45.
On remarque aussi que la médiane est la valeur de
l'abscisse du point d'intersection des courbes ECD et ECC.
IV. STATISTIQUE A UNE VARIABLE
Pour
comparer les résultats de séries statistiques, les paramètres de position
(mode, médiane , moyenne) sont parfois insuffisants,
en particulier pour caractériser la répartition des valeurs autour de la moyenne.
Pour cela, on utilise des paramètres dits de dispersion
: ce qui correspond à deux calculs lesquels ? l'étendue de la série et l'écart type.
¶ Calcul de l'étendue
A
quoi est égal le calcul de l’étendue ?
L'étendue de la série est égale à
la différence entre la plus grande valeur observée du caractère et la
valeur la plus petite.
· Calcul de l'écart type
L'écart
type permet de connaître la répartition des valeurs du
caractère par rapport à la valeur moyenne du caractère
Une
petite valeur de l'écart type traduit une forte concentration des valeurs
autour de la moyenne.
Calcul
de la variance :
|
|
On
appelle variance V d'une série statistique le nombre : xi
: Valeurs du caractère ou centre des classes ni
: effectif de xi ou de la classe de centre xi N
: effectif total |
Calcul
de l’écart type : L'écart
type se calcule à l'aide la formule suivante :
![]()
lire : racine carrée de la variance.
ATTENTION
: Pour des valeurs du caractère regroupées en classe, on prend pour valeur du
caractère le centre de chaque classe et l'effectif correspondant à cette
classe.
Pour
calculer cette grandeur, il faut utiliser les fonctions statistiques de votre
calculatrice.