|
|
|
|
LES PRISMES.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
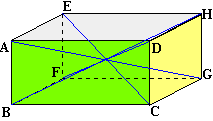
Définitions:
|
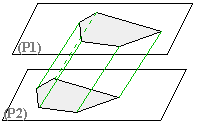
Un prisme est
un objet de l'espace qui a: -
deux faces de base parallèles (les plans (P1) et (P2) sont parallèles). Les bases sont des polygones. -
toutes ses arêtes latérales (en vert sur la figure) parallèles. La hauteur d'un
prisme est la distance
séparant les deux plans des bases |
|
Propriétés:
Les 2 bases
d'un prisme sont des polygones
(réguliers ou non). Ces deux polygones sont superposables.
Les faces latérales
sont des parallélogrammes.
On appelle prisme droit un prisme dont les arêtes
latérales sont perpendiculaires
aux plans des bases (les faces latérales de ces prismes sont donc des rectangles).
On appelle parallélépipède un prisme dont la base est un
parallélogramme.
On appelle parallélépipède droit un prisme droit dont la
base est un parallélogramme.
On appelle parallélépipède rectangle un prisme droit dont
les bases sont des rectangles.
Les arêtes latérales
ont toutes la même longueur.
Dessiner des
prismes droits:
Les arêtes cachées
sont représentées en traits pointillés. Une méthode de dessin dans l'espace est
exposée par ailleurs
A bases
triangulaires:
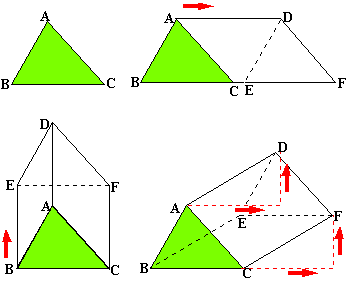
Pour représenter un
prisme droit à bases triangulaires, il suffit de dessiner deux triangles
superposables, "décalé" l'un par rapport à l'autre (horizontalement
ou verticalement ou les deux).
|
Le triangle ABC
étant dessiné, vous dessinez le triangle DEF en comptant les carreaux sur
votre feuille ou en mesurant avec un double décimètre, de façon que le
déplacement soit le même de A vers D, de B vers E et de C vers F. Ce
déplacement peut être par exemples: - 4cm
horizontalement pour AD, BE et CF. - 3cm verticalement
pour AD, BE et CF. - 4cm horizontalement
et 2cm verticalement pour AD, BE et CF. |
|
Remarque: Dans chacun
des trois cas ci-dessus nous avons représenté le prisme posé sur une face
latérale et non sur l'une de ses bases.
Le
parallélépipède rectangle:
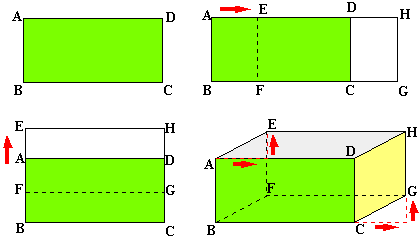
Pour représenter un
parallélépipède rectangle, il suffit de dessiner deux rectangles
"décalés" horizontalement ou verticalement ou dans les deux
directions.
|
Les bases ne sont
pas fixées: chacune des six faces peut jouer le rôle de base. Ici nous avons
choisi BCGF qui est représentée dessous. La méthode de
décalage est la même que pour le dessin du prisme à base triangulaire.
Comptez (ou mesurez) d'abord horizontalement, puis verticalement. |
|
Le cube:
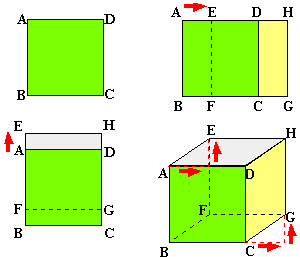
Nous représenterons
un cube de la même manière qu'un parallélépipède rectangle, à la seule
différence que nous commençons par deux carrés au lieu de deux rectangles.
|
Les six faces du
cube sont des carrés. Chacune peut être prise comme base. Ici encore, notez
bien que vous comptez (ou mesurez) d'abord horizontalement, puis
verticalement. Et rappelez vous
que les deux directions sont perpendiculaires... et que vous pouvez vous
déplacer dans les deux sens: vers la droite ou la gauche pour la direction
horizontale, et vers le bas ou le haut pour la direction verticale. |
|
Propriétés des
parallélépipèdes droits:
Le
parallélépipède rectangle:
Le parallélépipède rectangle
possède:
|
-
Six faces rectangulaires. Chacune de ces faces peut jouer le rôle de base. -
les douze arêtes sont égales 4 à 4: quatre longueurs (AD, BC,FG, EH), quatre
largeurs (AE, BF, CG, DH) et quatre hauteurs (AB, DC,HG, EF). -
Les douze arêtes sont parallèles 4 à 4. -
Chaque arête est perpendiculaire à deux faces opposées. Exemple: (AE) est
perpendiculaires aux faces ABCD et EFGH (nous considérons dans ce cas que ces
faces sont les bases du prisme, et comme les autres arêtes sont
perpendiculaires aux bases...) |
|
Remarque:
Nous pouvons
démontrer que les quatre diagonales intérieures sont égales et ont même milieu.
Nous utiliserons les propriétés des arêtes d'un parallélépipède rectangle (deux
droites parallèles définissent un plan: puisque vous travaillez dans un plan,
vous pouvez donc utiliser les théorèmes permettant de démontrer qu'un
quadrilatère est un rectangle (fiche
9 QRECT n°1) et les propriétés des diagonales de ces rectangles ).
- Démontrez que
AEGC, BDHF et BCHE sont des rectangles. Il suffit de montrer qu'ils possèdent
trois angles droits. Par exemple, pour AEGC: comme le côté (AE) est
perpendiculaire en A et E aux plans ABCD et EFGH (une face est contenue dans un
plan) alors (AE) est perpendiculaire à toutes les droites de ces plans passant
par A et E. Donc (AE) est perpendiculaire à (AC) et (EG). Même raisonnement
avec (CG) et la face ABCD...Comme AEGC a trois angles droits en A, C et E alors
AEGC est un rectangle. Faites la même chose avec BDHF et BCHE.
- Comme AEGC,est
un rectangle alors ses diagonales se coupent en leur milieu et sont égales.
Soit O milieu de [AG] et [EC] et AG=EC. De même avec les deux autres
rectangles:
[BH] et [EC] ont
même milieu et BH=EC (dans BCHE). Comme O est le milieu de [EC] alors O est
aussi le milieu de [BH].
[BH] et [DF] ont
même milieu et BH=DF (dans BDHF). Comme O est milieu de [BH] alors O milieu de
[DF]. O est donc le milieu des quatre diagonales
intérieures [AG], [BH], [EC] et [DF].
- Comme AG=EC et
BH=EC alors AG=EC=BH. Comme BH=DF et BH=EC=AG alors BH=DF=EC=AG. Les quatre diagonales intérieures ont donc la même
longueur.
Le cube:
Le cube possède:
- Six faces
carrées.
- Douze arêtes
de même longueurs.
- Les mêmes
propriétés que le parallélépipède rectangle.
Patrons:
Un patron d'un prisme
est un dessin sur un plan qui représente le prisme "déplié". Nous y
voyons donc toutes ses faces et ses bases en vraie grandeur.
le
parallélépipède droit:
Nous devons dessiner
deux bases qui sont des parallélogrammes et quatre faces latérales qui sont de
rectangles. L'exemple suivant donne le patron du parallélépipède droit ABCDEFGH
de base ABCD, dont les dimensions sont:
Longueur=3cm; largeur=2cm;
hauteur=4cm.
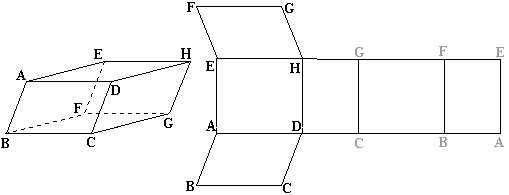
- Tracez d'abord
ADHE rectangle tel que AD=3cm et AE=4cm.
- Construire les
deux parallélogrammes (AB=EF=2cm).
- Construire les
trois autres faces qui sont des rectangles avec: DC=BA=2cm et CB=3cm.
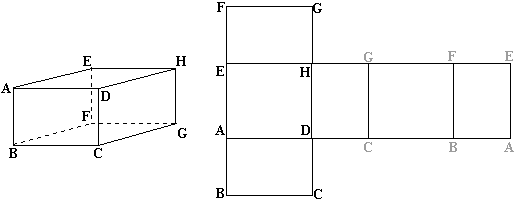
le
parallélépipède rectangle:
Le patron ressemble
fort à celui du parallélépipède droit avec deux bases rectangulaires au lieu de
deux parallélogrammes. Exemple avec les mêmes dimensions: L=3cm; l=2cm et h=4cm
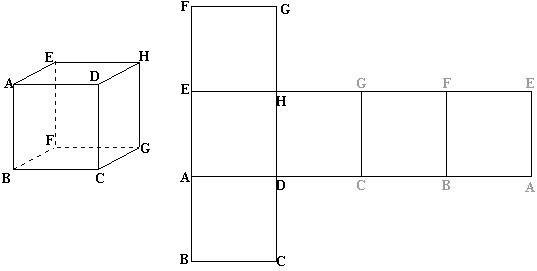
le cube:
Les quatres faces
sont des carrés. Voici un exemple de patron pour un cube d'arête 3cm:
Sections planes
d'un prisme droit:
Sur les figures
ci-dessous, les plans de section sont colorés en gris pour mieux les
distinguer.
Les
remarques ou démonstrations exposées ci-dessous ne concernent que les prismes
droits, c'est
à dire les prismes dont les arêtes latérales sont perpendiculaires aux bases.
Les polygones de base
ne sont pas forcément des quadrilatères (comme sur les figures ci-dessous);
le plan de
section est parallèle à la base:
|
La section est un
polygone superposable à celui de la base: sur la figure ci-conte IJKL a les
mêmes dimensions (angles et côtés) que ABCD et donc le même périmètre et la
même aire. Les côtés du
polygone de section (IJKL sur le dessin ci-contre) sont parallèles aux côtés
des polygones des bases. |
|
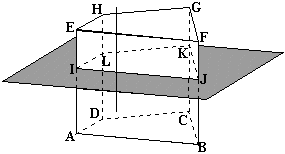
Le plan de
section est perpendiculaire aux bases:
|
Dans ce
cas: La section est toujours un rectangle. Sur la figure
ci-contre: IJKL est la section du prisme droit ABCDEFGH par un plan
perpendiculaire aux plans des bases. Comme les plans des
bases sont parallèles alors les droites d'intersection (JK) et (IL) avec le
plan de section sont parallèles (voir les propriétés dans l'Espace). Le prisme étant
droit, les faces ABFE et DCGH sont perpendiculaires au plan de la base ABCD. Comme le plan de
section et les plans des faces ABFE et DCGH sont perpendiculaires au plan de
ABCD alors leurs intersections (les droites (IJ) et (LK) ) sont des droites
perpendiculaires au plan de ABCD. Comme (IJ) et (LK) sont perpendiculaires au
plan de ABCD alors elles sont parallèles entre elles et perpendiculaires à
(IL) qui est une droite du plan ABCD passant par leur pied. Comme IJKL a ses
côtés (JK) et (IL) d'une part et ((IJ) et (LK) d'autre part parallèles deux à
deux alors IJKL est un parallélogramme. Comme IJKL est un
parallélogramme qui possède un angle droit en I (et même aussi en L) alors
IJKL est un rectangle. |
|
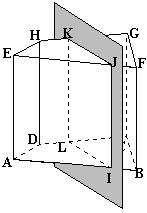
Remarque:
Si le plan de section
contient l'une des arêtes latérales alors le plan de section est
perpendiculaire aux bases. En effet, les arêtes d'un prisme droit sont
perpendiculaires aux plans des bases et le théorème concernant un
plan contenant une droite perpendiculaire à un autre plan s'applique;
Formules:
Nous ne donnons
ici que les formues pour les prismes droits (parallélépipèdes ou non).
La hauteur d'un
prisme droit est la distance entre ses deux bases (distance entre deux plans).
Aire
latérales=Somme
des aires des rectangles constituant les faces latérales
ou (mieux): Aire latérale=Périmètre de la
base*hauteur
Aire
totale=Aire
latérale+aire des bases
Volume=Aire de la base*hauteur