Pré requis:
|
Fraction équivalente |
|
|
Produit en croix |
|
|
|
|
|
Pour professeur : LES PROPORTIONS (cours)
|
TEST |
COURS |
Interdisciplinarité
|
COURS
APRES le travail sur LES
PROPORTIONS suivent le travail sur les « GRANDEURS
PROPORTIONNELLES » ; voir les supports théoriques relatifs aux
domaines traités(interdisciplinarités)
CES OBJECTIFS sont « LES
PREALABLES » POUR POUVOIR TRAITER :
LA FONCTION dite « LINEAIRE » :
Avant
de travailler ces trois objectifs il est utile de lire le rappel suivant
concernant « la fraction ; les fractions »
RAPPEL de l’objectif QI2
Obj. QI 2
FRACTION « EQUIVALENTE » *(à
une autre fraction):
-*
Cette notion est très importante ; elle est la clef de voûte du travail sur la
proportion et les proportionnalités.
- « Equivalente » :
veut dire « de même
valeur »;donc deux fractions équivalentes sont des fractions qui ont la
même valeur.(racine latine :« équi » qui signifie « égal »)
- Remarque .
Des fractions (ou écriture
fractionnaire)peuvent représenter un même nombre:
exemple:
la division 48 / 12 = 4
20 / 5 = 4
4.8 / 1.2 = 4
4 / 1 = 4
on peut donc écrire que ![]() =
= ![]() =
= ![]() =
= ![]() = 4
= 4
A ) Deux
fractions séparées par le signe égale sont dites « fractions
équivalentes »
Modèle mathématique:
![]() =
=![]() (b et d sont
différents de 0)
(b et d sont
différents de 0)
B ) Des fractions équivalentes représentent un même nombre
on peut donc écrire que ![]() =
= ![]() =
= ![]() =
= ![]() = (
4) sont des fractions
équivalentes)
= (
4) sont des fractions
équivalentes)
C )
Procédure pour construction d’une fraction équivalente (à une fraction donnée)
Pour construire une
fraction équivalente à une fraction donnée il suffit de multiplier le
numérateur et le dénominateur de la fraction par un nombre entier.
Modèle mathématique:
on multiplie a et b par k ![]() =
=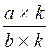 =
=![]()
IMPORTANT: MOYENS DE VERIFICATION
Pour
vérifier si deux fractions sont équivalentes ;Il y a deux solutions différentes :
Première
solution : on effectue les divisions et l’on compare !....
: On prend
une calculatrice ,on effectue les divisions relatives
à chaque fraction et l’on compare les deux résultats.(Il restera toujours un
doute notamment lorsque l’on divise des fractions irréductibles très proche ;
puisqu’elles n’ont pas de valeur décimale exacte).
(
Cette méthode peut être très utile pour classer des fractions ,les unes
par rapport aux autres)
exemple type I
Question: La fraction 11 / 15
est-elle équivalente à la fraction 13 / 17 ? (Si non ,on pourrait
alors demander de les classer par ordre ...croissant )
Réponse:
11 : 15 = 0.7333333
13 : 17 = 0.764705
conclusion: les fractions 11 /15
et 13 / 17 ne sont pas
équivalentes.
(Dans ce cas
,pour la question suivante , on peut écrire que 13 / 17
> 11 /15 )
exemple type II
Question :La fraction 22 /30
est-elle équivalente à la fraction
583/795 ?
Réponse:
22 : 30 = 0.733333333
583 :795 = 0.73333333
Conclusion :on ne peut conclure ,avec certitude ,on peut tout juste
déclarer : « elles pourraient
être équivalentes ».
Si on
ne peut conclure ,dans ce cas voir la solution
suivante
Deuxième
solution :on effectue « Le produit
en croix » (méthode la plus sûre)
Procédure permettant de vérifier si deux fractions sont équivalentes:
Pour
s’assurer (ou vérifier) que
deux fractions sont
équivalentes, il suffit de transformer l’égalité des deux fractions.
1°) On
transforme ce Modèle mathématique:
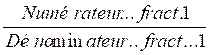 =
=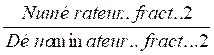
en une égalité de deux produits:
en ce modèle mathématique:
Numérateur..fract.1 x
Dénominateur. .fract 2
= Numérateur fract.2 x
Dénominateur fract
1
En résumé:
Deux fractions (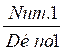 et
et 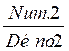 ) sont
équivalentes (c’est à dire) :
) sont
équivalentes (c’est à dire) :
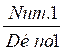 =
= 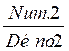 si Num.1 x
Déno.2 = Num.2 x Déno.1
si Num.1 x
Déno.2 = Num.2 x Déno.1
Lorsque nous aborderons la leçon
sur les proportionnalités on dira:
que le produit des extrêmes est égal au produit des moyens ,
(les extrêmes étants Num.1 et Déno.2, les moyens étants Déno.1 et Num.2)
SUITE
du rappel :
I )
Voir la division euclidienne : « si
le reste est égal à zéro ........ »
II )Voir l ’
objectif sur les fractions :
a) sur l’écriture d’une fraction
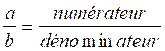
b) Construction de fractions équivalentes : 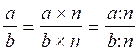
c) Addition
ou soustraction de fractions de même dénominateur se
souvenir que 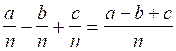
ATTENTION:
lorsque l'on additionne ou soustrait deux (ou plus) fractions de
même dénominateur , on n’a pas le droit
de modifier ce dénominateur ; donc dans l’exemple précédent on n’a pas le
droit de mettre comme dénominateur
« 3 n » ou « n3 »
REMARQUE IMPORTANTE :
LES PROPORTIONS METTENT EN JEU ,une
nouvelle opération mathématique,
NON PAS L ‘ADDITION ,LA SOUSTRACTION, LA DIVISION ou LA
MULTIPLICATION DE FRACTIONS , MAIS UNE CINQUIEME SITUATION MATHEMATIQUE
: L’EGALITE DE DEUX ( ou
plus) FRACTIONS.
COURS
Les
GRANDEURS PROPORTIONNELLES :
Définition
de « grandeur » :
On
appellera « grandeur » tout
nombre associé à une unité.
Exemple : 3litres,2,5mètres
La
division d’une grandeur sur une autre grandeur de même unité s’appelle un
« rapport »
Objectif n°
GP 1/3
Objectif n°
GP2/3
Objectif n°
GP3/3
OBJECTIF GP 1/3
Définition de l’objectif : ce qu’il faut savoir sur « rapport » ; « rapports
égaux » ; « suites de rapports égaux ».
COURS :
Rapport :
On appelle « rapport » la division d’un nombre
par un autre nombre.
Le modèle mathématique d’un « rapport » est « une
fraction ».
Rapports égaux :
On appelle « rapports égaux » des divisions
de deux nombres qui ont le même quotient
et dont le reste des divisions est nul .
Le modèle mathématique de deux rapports égaux est l’égalité de deux
fractions.
Traduction en langage
mathématique : 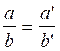
a’ : lire « a
prime »
b’
lire « b prime »
Suite de rapports égaux :
pour le mot « suite »
voir l ’ objectif
N° 1
Lorsque nous avons plus de deux
rapports égaux nous pouvons dire
que nous avons une « suite de
rapports égaux » , le quotient de chaque rapport
étant identique , c’est un nombre dit constant appelé « k ».
Traduction en langage mathématique :
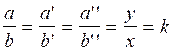
a’’ : lire « a »
seconde ; b’’ : lire « b » seconde.
Traduction en langage littéral :
« a sur b » est égal à « a prime » sur « b prime » est égal à
« a seconde » sur
« b seconde . »
remarque importante ,et à retenir :
par
convention ; « k » sera
toujours égal au rapport y sur x
; cette écriture est a mettre en relation avec
le « y » et le « x » du repère cartésien.
k = ![]() ; donc
inversement
; donc
inversement 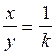 (par conséquence le rapport
x / y sera égal à la fraction
1 / k )
(par conséquence le rapport
x / y sera égal à la fraction
1 / k )
Exemple d’application : (Toujours se rappeler que ![]() = k)
= k)
on nous donne 4 rapports (![]() ;
; ![]() ;
; ![]() ;
; ![]() ) sont-il
égaux ?
) sont-il
égaux ?
Recherche :
A ) pour chaque rapport nous pouvons calculer
le «coefficient : k » :
premier rapport : 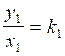 ;appliquons :
;appliquons : ![]() =1,5
=1,5
deuxième rapport : 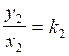 ;
appliquons :
;
appliquons : ![]() = 1,5
= 1,5
troisième rapport : 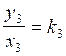 ; appliquons :
; appliquons : ![]() = 1,5
= 1,5
quatrième rapport : 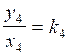 ;
appliquons :
;
appliquons : ![]() = 1,5
= 1,5
B ) analyse :nous constatons que k1 ; k2 ; k3 ;
k4 sont égaux
C) Conclusion : le coefficient K est identique pour chaque rapport ,nous pouvons écrire l’égalité suivante :
![]() =
= ![]() =
= ![]() =
= ![]()
Vérification : Pour vérifier si la suite de rapports est
une suite de rapports égaux il faut faire le produit en « croix » , chaque
égalité : ![]() =
= ![]() ( 3 fois4 égal 2
fois6)
( 3 fois4 égal 2
fois6)
; ![]() =
= ![]() (6 fois 6 égal 4 fois9 ) et
(6 fois 6 égal 4 fois9 ) et ![]() =
= ![]() (9 fois 9 égal 6 fois
13,5 ) .
(9 fois 9 égal 6 fois
13,5 ) .
Commentaire : quelque soit la
méthode de vérification elle est longue et parfois peut
fiable ;c’est à partir d’un constat que nous
allons appliquer une méthode plus rapide.
PROCEDURE :
Construire une autre fraction : avec les fractions équivalentes
données.
Cette autre fraction aura pour
numérateur :
le numérateur égal à la
somme des numérateurs et pour dénominateur égal
à la somme des dénominateurs .
(ATTENTION ! ! ! cette pratique n’est pas la somme de deux fractions
,c’est simplement la construction d’une fraction équivalente à des
fractions déjà équivalentes,se souvenir que dans
l’addition de deux fractions :
1°) elle n’est possible que si
les dénominateurs sont identiques.
2°)quand
les dénominateurs sont identiques,on fait seulement
l’addition des numérateurs)
Application :
les deux fractions suivantes sont
équivalentes (il faut toujours vérifier
l’équivalence)
![]() et
et ![]() ; pour obtenir une
autre fraction équivalente ,je fais les
deux additions 3+6 =9 (somme des numérateurs) et 2+4
= 6 (somme des dénominateurs); j ’ écris la nouvelle fraction
« équivalente » donc j’obtient la fraction
; pour obtenir une
autre fraction équivalente ,je fais les
deux additions 3+6 =9 (somme des numérateurs) et 2+4
= 6 (somme des dénominateurs); j ’ écris la nouvelle fraction
« équivalente » donc j’obtient la fraction ![]() .
.
Vérification :
si je fait la
division de 9 par 6 je trouve 1,5 ;
(valeur égale à k)
Par
extension :
Je peut opérer de la même façon avec toutes les fractions de la
« suite de fractions »
donnée :
soit la suite de fractions , sont-elle équivalentes ?
![]() =
= ![]() =
= ![]() =
= ![]() ;
;
(si les fractions données sont équivalentes, je peut construire une autre fraction équivalente qui aura
pour numérateur la somme des numérateurs et pour dénominateur la somme des
dénominateurs, ensuite je
vérifierai pour cela deux
solutions :
- la division du numérateur par le dénominateur pour trouver le « k ».
ce qui
me donne l’opération 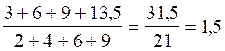
J’obtient une
fois encore la valeur « k » de
1,5
- Ou alors je prendrai une fraction donnée
au hasard et je ferai le produit en croix pour vérifier l’égalité des
produits.)
On remarque qu’avec des fractions dites
« égales » ,si on additionne les numérateurs
entres eux et si l’on additionne les dénominateurs entres eux ,et si l’on met
ces résultats sous forme de fraction ,on obtient une autre fraction égale aux
précédentes.
CONCLUSION :
Avec une suite de rapports égaux ,on forme un
autre rapport(ou fraction) égal à chacun d’eux
( de chaque rapport) qui
aura pour numérateur la somme des
numérateurs et pour dénominateur la somme des dénominateurs .
traduction en
langage mathématique :
si ![]() =
= ![]() =
= ![]() =
= ![]() ; alors on
a
; alors on
a 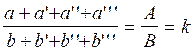
Commentaire : on peut donc dire qu’une suite de rapports (ou de grandeurs ) sont proportionnels si la somme des numérateurs
sur la somme des dénominateurs (de tous
les numérateurs et dénominateurs de ces
rapports) forme une proportion avec un des rapports de cette suite.
Procédure de vérification :faire
le produit en croix, (ou faire la
division pour les deux rapports et comparer le quotient ).
REPRESENTATION
GRAPHIQUE D’UNE SUITE DE RAPPORTS PROPORTIONNELS :
Voir
l’ objectif sur les repères ( Sauf cas particulier
et dans ce cas signalé nous travaillons
dans un repère cartésien orthonormé)
La représentation d’une suite de rapports non proportionnels est un ensemble de points non alignés ,dans un repère.;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() La
représentation d’une suite de rapports proportionnels est un ensemble de points
alignés, qui ont pour particularités de tous
trouver sur une droite
La
représentation d’une suite de rapports proportionnels est un ensemble de points
alignés, qui ont pour particularités de tous
trouver sur une droite
CONTROLE :
1.
Qu’est ce qu ’ « un rapport » ?
2.
Donner un modèle mathématique d ’ un rapport.
3.
Qu’appelle-t-on « rapports
égaux » ?
4.
Donner un modèle mathématique de
« rapports égaux »
5.
Donner une suite de rapports égaux.
6.
Que peut-on former à partir d’une
suite de rapports égaux ?
7.
Traduire en langage mathématique ce que vous avez énoncé précédemment
8.
Combien a - t - on de moyens de vérifier si
deux rapports sont proportionnels ?
Donner la procédure d’exécution
pour chaque ,vous pouvez vous aider de nombres)
Comment peut-on vérifier si une
suite de nombres (ou de grandeurs) sont proportionnels ?
9.
(Donner un exemple).
10.
Que signifie l’écriture mathématique suivante ?
si
![]() =
= ![]() =
= ![]() =
= ![]() ; alors on
a
; alors on
a 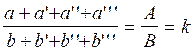
EVALUATION :
Construire une suite de deux rapports non égaux ; justifiez
a) avec
des nombres
b) avec
des lettres
Construire une suite de deux
rapports égaux ; justifiez.
a) avec
des nombres
b) avec
des lettres
Objectif : GP 2/3...
Intitulé : LA PROPORTION. LA
QUATRIEME PROPORTIONNELLE :
PROPORTION :
On appelle « proportion » l’égalité se deux rapports.
Relations qui existent entre les mots : fraction ;
rapport ; rapports égaux, fractions équivalentes ; proportion :
fraction = rapport
égalité
de deux fractions = fractions équivalentes
fractions équivalentes = rapports égaux
rapports égaux
= égalité de deux fractions
rapports égaux
= proportion
donc une proportion c’est l’égalité de deux
fractions.
Modèle mathématique :
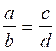
RAPPEL
sur les fractions équivalentes :
En résumé:
Deux fractions (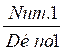 et
et 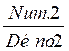 ) sont
équivalentes (c’est à dire) :
) sont
équivalentes (c’est à dire) :
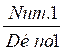 =
= 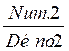 si Num.1 x
Déno.2 = Num.2 x Déno.1
si Num.1 x
Déno.2 = Num.2 x Déno.1
applications algébriques :
soit l’égalité 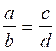 ont
peut donc écrire a
ont
peut donc écrire a
![]() d = c
d = c ![]() b
b
Commentaire : d’une proportion on peut obtenir par
transformation l’égalité de deux
produits
Cette nouvelle égalité peut à nouveau se transformer dans le
but de trouver une autre égalité permettant
de trouver a= .....;
b=...... ; c=....... ; ou d =....... ;
transformations :
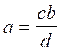 ;
; 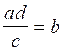 ;
; 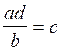 ;
; 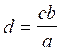
applications numériques : Trouver la valeur
de « x » , (pour que l’égalité
reste vraie)
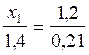 ;
; 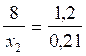 ;
; 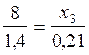 ;
; 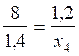
AUTRE
VOCABULAIRE utilisé :
L’écriture mathématique: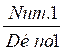 =
= 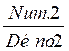 si Num.1 x
Déno.2 = Num.2 x Déno.1
si Num.1 x
Déno.2 = Num.2 x Déno.1
sera
remplacé par :
pour la
première fraction :
le
numérateur de la première fraction
s’appellera : Extrême 1
le
dénominateur de la première fraction
s’appellera : Moyen 1
pour la
deuxième fraction :
le
numérateur de la deuxième fraction
s’appellera : Moyen 2
le
dénominateur de la deuxième fraction
s’appellera : Extrême 2
Ce qui donne :
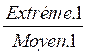 =
= 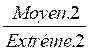 si Extréme.1 x
Extréme.2 = Moyen .2 x Moyen.1 ;
si Extréme.1 x
Extréme.2 = Moyen .2 x Moyen.1 ;
Nous
pouvons énoncer :
I ) Dans une
proportion, le produit des extrêmes est égal aux produits des moyens.
Traduction
mathématique :
si ![]() =
= ![]() alors ad = cb
alors ad = cb
II)
Dans une
proportion, on peut permuter les « extrêmes »« ( l’égalité reste vraie)
traduction mathématique
si ![]() =
= ![]() alors
alors ![]() =
= ![]()
III)
Dans
une proportion, on peut permuter les « moyens » ,(l’égalité
reste vraie)
traduction mathématique
si ![]() =
= ![]() alors
alors ![]() =
= ![]()
Remarque :
Lorsque l’on connaît 3 valeurs sur 4 ,dans une
proportion, on peut trouver la « quatrième » valeur . On dira «
rechercher la quatrième proportionnelle. »
Dans une proportion comment
appelle-t-on :
le
numérateur de la première fraction
le
dénominateur de la première fraction
le
numérateur de la deuxième fraction
le
dénominateur de la deuxième fraction
Qu’appelle-t-on « proportion » ?
A
quoi est égal deux rapports égaux ?
Quel est le modèle mathématique pouvant représenter des rapports égaux ?
On
donne deux rapports égaux :
Comment nomme-t-on le numérateur de la première et le dénominateur de la
seconde fraction ?
Comment nomme-t-on le dénominateur de la
première et le dénominateur de la seconde fraction ?
Enoncer les règles faisant intervenir les extrêmes et les moyens.
(donner un modèle
mathématique et ensuite accompagner ces modèles d’application numérique.)
Dans quel cas dit-on que l’on recherche la quatrième
proportionnelle ?
1°) De l’égalité 3,4 x 7,8 = 2,4
x 11,05 ; déduire toutes les proportions possibles.
2°)Idem que ci dessus :
6,03 x
0,25 =
4 ,5 x 0,335
3°) Calculer dans chacun des cas
suivants :
x![]() 0,37 = 8,88 ; 6,5 x = 46,15
0,37 = 8,88 ; 6,5 x = 46,15
11,2 = 3,2 x
7,56 = x ![]() 0,9
0,9
4°) Calculer
x dans chacun des cas suivants :
![]() =
= ![]() ;
; ![]() =
= ![]() ;
; ![]() =
= ![]() ;
;
5°)
Calculer « x » dans chacun des
cas suivants :
![]() =
= ![]() ;
; ![]() =
= ![]() ;
; ![]() ; =
; = ![]() ;
;
6°)
Calculer « x » dans chacun des
cas suivants :
![]() =
= ![]() ;
; ![]() =
= ![]() ;
; ![]() =
= ![]() ;
;
7°)
Calculer « x » dans chacun des
cas suivants :
![]() = 12 ;
= 12 ;
![]() = 4 ;
= 4 ; ![]() = 0,75
= 0,75
8°)
Calculer « x » dans chacun des
cas suivants :
12= ![]() ; 3,7 =
; 3,7 = ![]() ; 2 =
; 2 = ![]() ; 1,3 =
; 1,3 = ![]() ;
;
Interdisciplinarité :
Des
connaissances e n sciences sont nécessaires pour
comprendre le travail demandé ; (à
vous de vous informer :
1°) Calculer
la mesure de la d.d.p. aux bornes d’un résistor dans
les cas suivants :
|
calibre |
Echelle |
lecture |
|
|
3 V |
[ 0 ; 30
[ |
22 divisions |
|
|
10 V |
[ 0 ; 100
] |
57 divisions |
|
|
300 V |
[ 0 ; 30
[ |
25 divisions |
|
2°) Quelle
est l’intensité du courant traversant le circuit ?
|
Calibre |
Echelle |
lecture |
|
1 A |
( 0 ; 100
) |
83 divisions |
|
0,1 A |
( 0 ;
100) |
57 divisions |
3°) Une voiture consomme 18,4 l d’essence pour
effectuer le trajet Paris - Caen ( 230 km) .Quelle sera sa consommation pour effectuer le
trajet Paris - Cherbourg
long de 340 km ?
Que devons nous admettre pour résoudre le problème ?
4°) La masse
et le volume d’un corps sont deux grandeurs directement proportionnelles .Le
coefficient de proportionnalité s’appelle la « masse volumique » du
corps.
a) Calculer le volume d’un corps de masse 52 kg dont la masse volumique est de 23 kg /dm3
b) Calculer la masse d’un corps de volume 3,5 dm3 dont
la masse volumique est de 7,8 kg / dm3.
CONTROLE :
(corrigé)
Dans
une proportion comment appelle-t-on :
le numérateur de la première fraction s’appellera : Extrême 1
le dénominateur
de la première fraction s’appellera : Moyen 1
pour la deuxième fraction :
le numérateur de la deuxième fraction s’appellera : Moyen 2
le dénominateur
de la deuxième fraction s’appellera : Extrême 2