Auteur : WARME R. DOSSIER TRAVAUX AUTO FORMATIFS .
NOM : ………………………………	Prénom : …………………………..	Classe :…………………..
Année scolaire : ………………………	Dossier pris le : ……/………/………	Validation de la formation : O - N Le : …………………………………….. Nom du formateur  : ……………………
ETABLISSEMENT : …………………………………………..

Leçon	Titre
N°23	TRAVAUX d ’ AUTO - FORMATION sur LA FONCTION LINEAIRE

TRAVAUX N°23 d ’ AUTO - FORMATION : CONTROLE

a) Quelle condition doit remplir un « tableau numérique  » pour être le représentant d’une fonction ?

b) Que désigne le mot « variable » ?

1°) Donnez le modèle mathématique de l’équation représentant la fonction linéaire.

2°) Que peut-on représenter à partir d’une équation représentant la fonction linéaire ?.

3°) Soit la notation « ax » , comment nomme - t - on les facteurs ?

4°) Donnez la forme des couples qui forment eux mêmes le graphe de la fonction linéaire.

5°) Donner forment du graphe de la fonction linéaire. ( donner les deux couples particuliers)

6°) Représenter le tableau de « proportionnalité ; précisez ce qu’il « contient ».

7° ) « a » (dans le produit de facteurs associés à la fonction linéaire) possède trois appellations , quelles sont - elles ?

8° ) Définissez « la représentation graphique »

précisez ,en citant les caractéristiques principales ; placer les dans un repère cartésien.

9° ) Comment reconnaît - on une fonction dite « linéaire » ?

TRAVAUX N°23 d ‘ AUTO - FORMATION EVALUATION

Soit les fonctions :

y1 = 2x

y2 = - 2x

y3 = -

1°) Dans un repère cartésien orthonormé ; Faire la représentation graphique de chaque fonction .

A l' équation y1 = 2x	On associe la droite D1 (lire :droite indice 1)
A l' équation y2 = - 2x	On associe la droite D2 (lire :droite indice 2)
A l' équation y3 = -	On associe la droite D3 (lire :droite indice 3)

2°) En étudiant le graphique , donner les coordonnées du point d’intersection des deux droites D₁ et D₂;

3°) tracer D₃

Ensuite : avec un rapporteur donner la valeur de l’angle faite entre les droites D₁ et D₃ .

Quel commentaire pouvez-vous avoir sur la position des droites l’une par rapport à l’autre ?

4° ) Faite le calcul du produit a₁ par a₃ .

5°) tracer la droite d'équation y₄ =

mesurer l’angle fait par D₂ et D₄ ; faire le produit a₂ a₄

6°)comparer les résultats de la question 4° et 5°; quelle conclusion peut - on en tirer ?

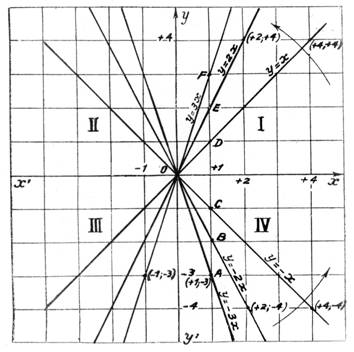
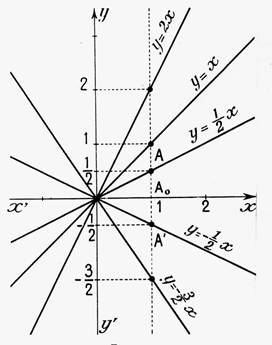
Voir les représentations graphiques ci dessous.

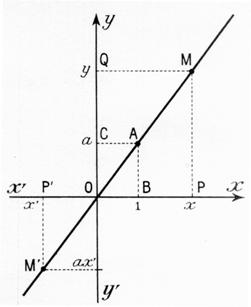
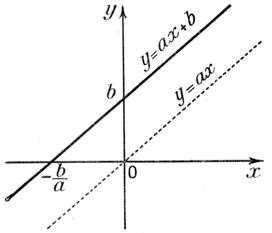
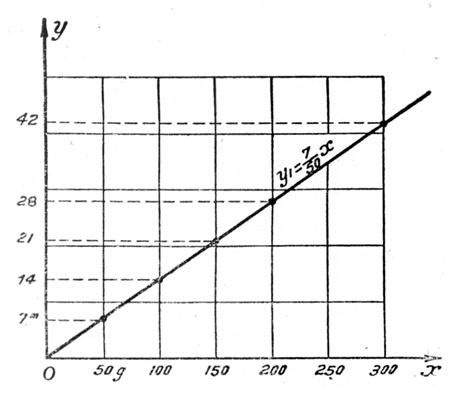
Exemples de représentations graphiques d’une « fonction linéaire » .

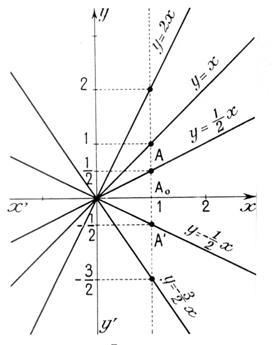
Exemples de tracés en fonction de l’équation.
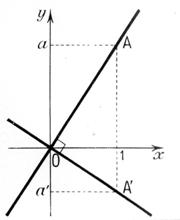
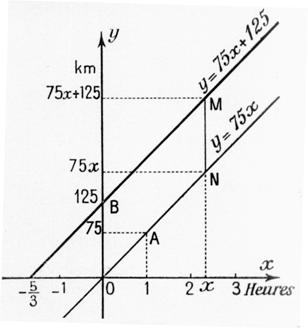
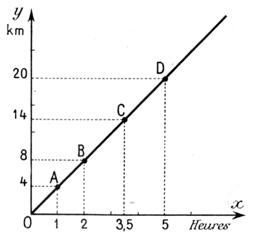
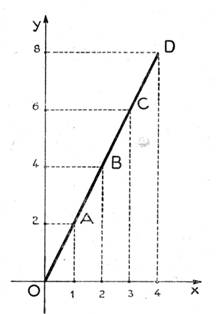
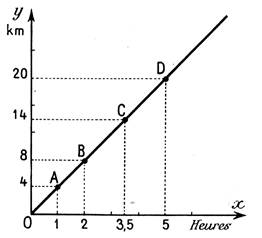
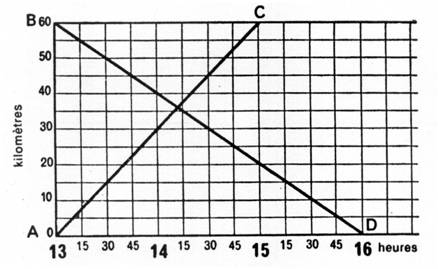
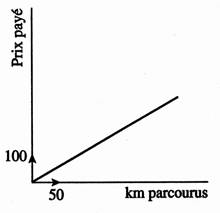
Exemples de situations - problèmes représentées par un graphique. ( à vous d’interpréter ces graphiques )
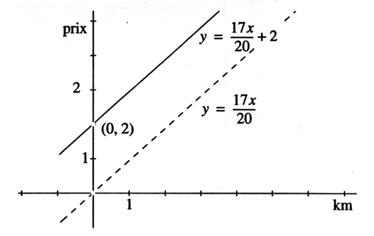
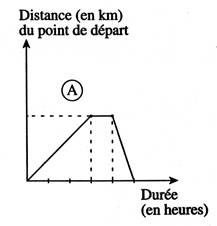
( ne pas s’intéresser à la droite BD)
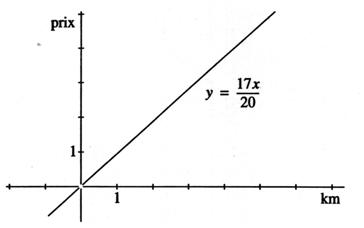
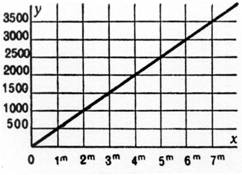
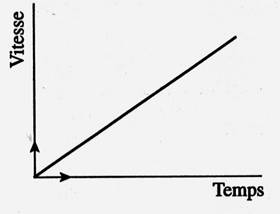
	Ne s’intéresser qu’ à la droite qui part de l’intersection du repère.»
Ces exercices de lecture de graphiques seront repris après que l’étude de la fonction affine ne soit faite.