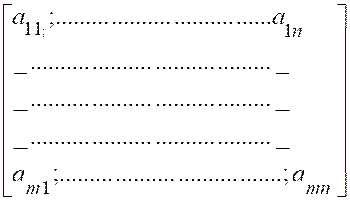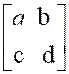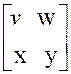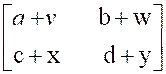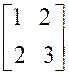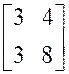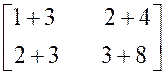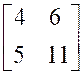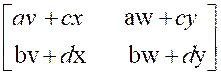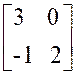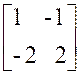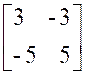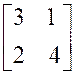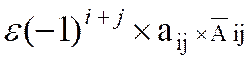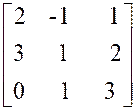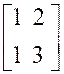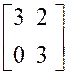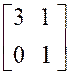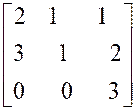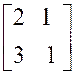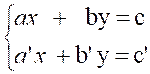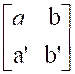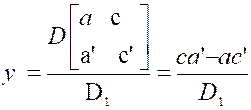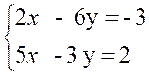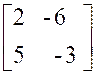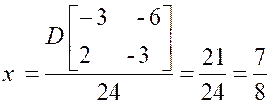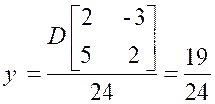A ) Une matrice est de la forme :

			« a₁₁ » représente un coefficient de la matrice , se situant à la 1^ère ligne , 1^ère colonne. »
			« i » = n° de ligne
	Un coefficient est repéré dans la matrice par la formule a_{i j}
			« j » = n° de colonne

	· Une matrice ayant le même nombre de lignes et de colonnes est appelée : une « MATRICE CARREE »
	· Une matrice comportant 2 lignes et 2 colonnes est appelée : une « MATRICE D’ORDRE 2 »
	· Une matrice comportant 3 lignes et 3 colonnes est appelée : une « MATRICE D’ORDRE 3 »
	Etc.………………………

B) Calcul d’une somme de matrices ( d’ordre 2)

	On appelle « somme de la matrice » par la matrice la matrice

	Exemple : calculer : + = …………. ; = =

C) Calcul d’un produit de matrices ( d’ordre 2)

	On appelle « produit de la matrice » par la matrice la matrice

	Exemple : calculer : x = …………. ; = =

D) Calcul du déterminant d’une matrice ( d’ordre 2)

	Le déterminant d’une matrice est noté D= ( a x d ) - ( b x c)
	Exemple : D = ( 3 ) ( 4) - ( 1 ) ( 2) = 10

E) Calcul du déterminant d’une matrice ( d’ordre 3 ou « n » )

	= ( applicable à 1 ligne de la matrice choisie arbitrairement)
		« i » = n° de ligne « j » = n° de colonne
	« a _ij » = coefficient de la « i^ème » ligne j ^ième colonne. « » déterminant que l’on obtient de la matrice de départ , en supprimant la i^ème ligne et la j ^ième colonne.
	Exemple :
	= ( -1) ¹⁺¹ ( 2 ) + ( -1) ¹⁺² ( - 1 ) + ( -1) ¹⁺³ ( 2 ) = 2 + 9 + 3 = 14
D


	= ( -1) ^{3 +3} ( 3 ) = - 3
D


F) Résolution de système d’équations « x » matrices .

	Soit le système :
	1°) Calcul du déterminant n°1 : D₁ = a b’ – b a’
	2°) Calcul de « x » et « y » . et

	Exemple : Soit le système :
	1°) Calcul du déterminant n°1 : D₁ = (2 x) ( - 3 ) – (5 x) ( - 6 ) =
	2°) Calcul de « x »

	3°) Calcul de « y » .