|
|
||
|
|
|
|
|
i9 |
Les égalités |
:i |
|
|
|
|
|
|
|
|
III
)
LECON n°5 : Equations contenant plusieurs
« x » répartis dans les deux membres.
Soit
à résoudre l’équation 5x + 4 - x
= 6 + 10 + 2 x
Procédure :
a) On fait passer les termes en « x »
dans le premier membre et les termes connus dans le second membre.
5x - x - 2 x = 6 + 10 - 4
b) on regroupe les termes 5 x - 3 x
= 16 - 4
soit 2x = 12
c) on calcule « x » d ’
où 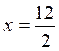
d)
conclusion : x = 6
Quand
les « x » sont parsemés, on les rassemble dans un membre et on chasse les termes connus dans l’autre.
Remarque : Supposons que nous ayons voulu
réunir les « x » à droite, on
eût obtenu :
5x + 4 - x = 6 + 10 + 2 x
+4
- 6 - 10 = - 5x
+ x + 2x
En
essayant d’effectuer les calculs on eût
abouti à une difficulté.
Cela donne
- 12 = - 2x
Il
faut rassembler les « x » du côté où leur total est aisé à effectuer.
Autre
façon :
(on considère que tous les nombres sont des nombres relatifs)
On transforme les deux membres en « somme algébrique ».
Soit
à résoudre l’équation 5x + 4 - x
= 6 + 10 + 2 x
On
transforme les expressions en sommes
(+ 5x) + (+ 4) + (- x) = (+ 6) + (+ 10) + (+ 2 x)
On
regroupe les termes connus dans le second membre et les termes inconnus dans le
premier membre.
(+5x)
+(- x) + ( -2x)
=(+ 6) + (+10) + (-4)
on
regroupe les « x » et on calcule dans le deuxième membre.
(+ 2x) =
(+12)
x = (+6)
|
Titre |
|
|
N°5 |
TRAVAUX d
’ AUTO - FORMATION sur Equations contenant plusieurs « x » dans les deux membres. |
Dans une équation, quand plusieurs
« x » sont précédés du
signe « + ou - » répartis
dans les deux membres quel faut-il faire ?
Exercices : Résoudre les équations
suivantes :
|
I) |
4x - 3 + 7 x + 4
- 10 x = 7 |
|
· a |
6x + 7 - x = 13 - x |
|
II)
|
13 x - 4 - 8 x - 2 + 8 = 12 |
· b |
3x + 7 = 5x + 5 |
|
|
III)
|
3x - 7 = 9
+ x |
· c |
7x - 14 - 5x = 2 + 6x + 2x |
|
|
IV)
|
4x + 8 = 18 - x |
· d |
3x - 4+ 2x = 6x - 14 |
Pb : 3 fois la distance de la gare aux halles
moins 7 hectomètres valent autant que cette distance plus 9 hectomètres.
Calculer la distance.
CORRIGE :
Exercices : Résoudre les équations
suivantes :
|
|
4x - 3 + 7 x + 4
- 10 x = 7 |
|
· a |
6x + 7 - x = 13 - x |
|
|
13 x - 4 - 8 x - 2 + 8 = 12 |
· b |
3x + 7 = 5x + 5 |
|
|
|
3x - 7 = 9
+ x |
· c |
7x - 14 - 5x = 2 + 6x + 2x |
|
|
|
4x + 8 = 18 - x |
· d |
3x - 4+ 2x = 6x - 14 |
Pb : Pb : 3 fois la distance de la gare
aux halles moins 7 hectomètres valent autant que cette distance plus 9
hectomètres. Calculer la distance.