Pré requis : « @
PYTHAGORE TRACES »
|
Interdisciplinarités. |
|
|
N°20 |
CORRIGE sur PYTHAGORE théorème ; la
Propriété de PYTHAGORE et sa réciproque. |
|
|
|
Série II
|
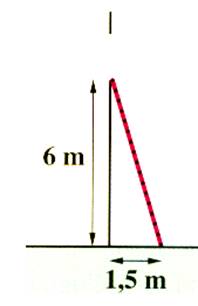
N°2 : Quelle longueur doit mesurer une
échelle pour atteindre une fenêtre située à 6 m. Si on lui donne 1,5 mètres
de pied ? D’après Pythagore : (Longueur de l’échelle )
² = 6 ² + 1,5 ²
(Longueur de l’échelle )
² = 36 + 2,25
(Longueur de l’échelle )
² = 38,25 Racine carrée de 38 ,25 = 6,18 4658438 L’échelle devra mesurer plus de 6,18 m |
|
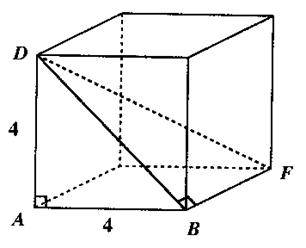
Géométrie dans l’espace : (redessiner les
figures à l’échelle « 4 »)
|
Calculer la diagonale DB du cube au dixième près. DB²= DA< ² + AB² DB² = 4²+ 4² DB² = 32 DB =
DB = 5,656854………. DB =
5,7 à 0,1 prés Calculer la diagonale DF du cube au dixième près. DF²
= DA² + AF² Puisque c’est un cube : DB = AF Donc
DB² = AF² = 32 Donc : DF² = 4² + 32 DF² =
16 + 32 DF² = 48 DF = DF = 6 , 9282 DF = 6,9 à 0,1 prés . |
|
|
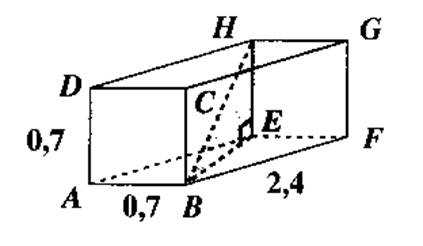
N°3
Calculer la longueur de la diagonale
du segment BH , au dixième près. AB = 7 cm
; BF = 24 cm EB ² = (AB)
² + ( BF)² EB ² = (0,7 ) ² + ( 2,4 )² EB ² = 49
cm² +
576 cm² ( EB)² = 625 cm² EB= 25 cm. (HB)² =
(EB)² + (EH)² (HB)² = 625
cm² + 49 cm² (HB)² = 674 cm² (HB) = 26
cm |
|
|
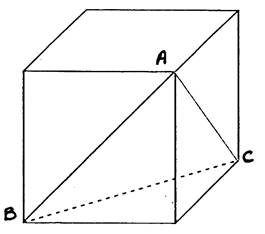
N°4 : Le cube à 5 cm d’arête. Calculer BA , AC et BC. Quelle est
la nature du triangle BAC ? (BA)² = (25)² + (25)² =
625 + 625 =
1250 BA
= 35,35 AC = 35,35 BC ²
= 1250 + 1250 = 2500 BC = 50 |
|