|
Auteur :
WARME R.
INFORMATIONS
« LIVRE » ; document neutre. Pour accéder au
document interactif il faut posséder le code d’entrée.
|
|||||
|
NOM : ……………………………… |
Prénom : ………………………….. |
Classe :………………….. |
|||
|
Année scolaire : ……………………… |
Dossier
pris le : ……/………/……… |
Validation
de la formation : O -
N Le : …………………………………….. Nom
du formateur : …………………… |
|||
|
ETABLISSEMENT :
………………………………………….. |
|||||
|
Leçon |
Titre |
|
||
|
N°1 |
|
|||
CHAPITRES
|
INFO plus !!!! @ |
|
|
INFO plus !!!!! @ |
|
|
INFO plus !!!! @ |
|
|
INFO plus !!!! @ |
|
1°) ECRITURE DECIMALE D’UN NOMBRE |
a)
Définition : Un nombre entier @ est un
alignement horizontal de chiffres, écrit en liste ils sont séparés par des points
virgules
Exemples : 6 ;
7 ; 10 ; 1456 ; 14568342
b)
Définition :Un nombre
décimal @.est un
alignement horizontal de chiffres
séparés par une virgule.
Exemples : 3542,68 ; 0,564 ; 103,05
Le nombre décimal se
compose de deux parties :
Sa
partie entière est : « 3542 » ( partie à gauche de la virgule)
Sa
partie décimale est : « 68 » ( partie à droite de la virgule)
> Se souvenir que 3542,68 est la somme de deux nombres :
3542 et 0,68
> Si la partie décimale ne comporte que des zéros dans ce cas
on considérera que l’écriture des
nombres (par exemple ) 34 ; 34 , 0 ; 34,00 … sont « équivalentes »
.
Dans une liste de
nombres , les nombres entiers et
/ou décimaux sont séparés par un point -
virgule.
c)
Comparaison de nombres :
« comparer » : Comparer : c’est Trouver le plus grand ou le plus petit
Pour pouvoir
comparer des nombres, ou faire des
opérations , il faut savoir ce que représente la position de chaque chiffre.
Pour cela on utilise un tableau .
Tableau de numération ( des nombres décimaux ): (Il faut savoir le dessiner)
Il comprend deux parties : la partie entière et la
partie décimale.
|
Partie entière (multiples ) @ |
Partie décimale @
(sous multiples) |
||||||||||
|
millions@ |
mille@ |
unités@ |
centièmes@ |
millièmes@ |
|||||||
|
C |
D |
U |
C |
D |
U |
C |
D |
U |
|
|
|
|
Ex. |
|
|
|
|
3 |
5 |
4 |
2 |
6 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 Tout nombre décimal peut se décomposer ainsi :
Tout nombre décimal peut se décomposer ainsi :
3542,68 = 3 ![]() 1 000 + 5
1 000 + 5![]() 1 00 + 4
1 00 + 4![]() 1 0 + 2
1 0 + 2![]() 1 + 6
1 + 6![]() 0,1 + 8
0,1 + 8 ![]() 0,0 1
0,0 1

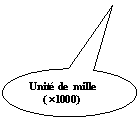

le chiffre « 3 » appartient à l’unité de
mille ; « 5 » appartient aux centaines d’unité ; le chiffre
« 4 » aux dizaines d’unités , le chiffre « 2 » aux unités
d’unités ; le « 6 » aux dixièmes d’unité ; et le
« 8 » aux centièmes d’unités.
|
?Activité n °1: |
Tableau à
connaître :
|
millions |
mille |
unités |
Valeur décimale : |
|||||||||
|
C |
D |
U |
C |
D |
U |
C |
D |
U |
dixièmes |
centièmes |
millièmes |
|
|
Ex. |
|
|
|
|
3 |
5 |
4 |
2 |
6 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En vous aidant de l’exemple
ci dessus décomposer les nombres suivants :
1236,54 =
14 557, 354 =
14 788 ,708 =
e) Savoir : Ecrire
un nombre en lettre : ( vis versa )
|
Adjectifs
numéraux |
|||||||
|
0 |
Zéro |
10 |
Dix |
20 |
Vingt
|
71 |
Soixante
et onze |
|
1 |
Un |
11 |
Onze |
21 |
Vingt
et un |
72 |
Soixante
- douze |
|
2 |
Deux |
12 |
Douze |
22 |
Vingt-deux |
80 |
Quatre-vingts |
|
3 |
Trois |
13 |
Treize |
30 |
Trente |
90 |
Quatre-vingt-dix |
|
4 |
Quatre |
14 |
Quatorze |
31 |
Trente
et un |
100 |
Cent |
|
5 |
Cinq |
15 |
Quinze |
32 |
Trente
deux |
1 000 |
Mille |
|
6 |
Six |
16 |
Seize |
40 |
Quarante |
10 000 |
Dix
mille |
|
7 |
Sept |
17 |
dix-sept |
50 |
Cinquante |
1 000 000 |
Un million |
|
8 |
Huit
|
18 |
dix-huit |
60 |
Soixante |
10 000 000 |
Dix
millions |
|
9 |
Neuf
|
19 |
dix-neuf
|
70 |
Soixante-dix |
|
|
Les
adjectifs numéraux sont invariables sauf « vingt » et
« cent » s’ils sont multipliés
mais pas s’ils sont suivis d’un nombre .
f)
Les règles d ‘orthographe sont :
Million et milliard prennent la
marque du pluriel.
exemple : 67 140 000
s’écrit soixante sept millions
Mille est invariable
exemple : 67 140 000
s’écrit soixante sept millions cent quarante mille.
Cent prend la marque du
pluriel ; s’il est le dernier mot , autrement il est invariable.
(cas particulier : « cent » est invariable quand il correspond à une
numérotation : page : trois cent)
exemple :
600 s ’ écrit « six cents»
637
s’écrit « six cent
trente sept » ;
Vingt prend la marque du
pluriel ; s’il est le dernier mot
. Sinon il est invariable.
exemple :
80 s ’ écrit « quatre vingts »
87
s’écrit « quatre vingt
sept »
|
Autres
exemples : |
400 : quatre
cents ; 402 : quatre cent deux ; 120 : cent
vingt ; 85 : quatre-vingt cinq ; 2 654,28 : deux
mille six cent cinquante-quatre unités
et vingt-huit centièmes
éventuellement
voir rappel cd ³ dans N@
APPLICATION : ce qu ‘il faut savoir
pour remplir des chèques :
- L ’ unité de base monétaire est l’
« Euro » (
symbole € ) ( ³ Euro) @
- Les sous - multiples utilisés sont le dixième et le centième d’ Euro
.
- Le centième d’euro s ’ appelle le « cent » ou « centime » .
Activité : remplir le chèque
pour une valeur de 175,48 €
Mettre un chèque fac-similé
|
i9 @ |
INFO plus !!!!! @ |
a)
|
Définition : Comparer
deux nombres , c’est chercher lequel est le plus grand ( ou le plus petit) ou
dire s’ils sont égaux. |
b) Les signes de
« comparaisons » sont :
< ; > ;
=
|
« Plus
petit » se traduit par le signe |
< |
|
« Egal » se
traduit par le signe |
= |
|
« Plus
grand » se traduit par le signe |
> |
Exemples :
|
Au lieu d’écrire : |
On écrira : |
|
« 4,9 est plus petit que 5 » |
4,9 <
5 On Lira :
quatre virgule neuf est plus petit que cinq. |
|
« 1,9 est égal à la fraction décimale |
1,9 = On lira : un
virgule neuf est égal à la fraction
dix neuf dixième |
|
« 3,7 est plus grand que 3 » |
3,7 > 3. On lira :
trois virgule sept est plus grand que
trois . |
c) Méthode de comparaison
de deux nombres entiers naturels
|
Cd ³Comparaison de deux nombres entiers ( N ) : @ Il faut répondre à la question : lequel
est plus petit ? ; lequel
est plus grand ? ; sont-ils
égaux ? |
|
Méthode : Le plus petit est celui qui a le moins de
chiffres . S’ils ont le même nombre de chiffres , on
compare chiffre à chiffre à partir de la gauche. |
|
Exemples : |
a) comparons : 567 et
89 :
567 > 89 ( car 567 à 3
chiffres et 89 deux chiffres)
b) 389 et 391 : 391 > 389 ( car dans
389 le chiffres des dizaines est
plus petit que dans 391)
d) Méthode de comparaison de deux nombres décimaux
positifs :
|
Cd ³Comparaison de deux nombres décimaux positifs ( D
) : @ Il faut répondre à la question : lequel
est plus petit ? ; lequel
est plus grand ? ; sont-ils
égaux ? |
|
Méthode : Le
plus petit est celui qui a la partie entière la plus petite . S’ils ont
la même partie entière , on compare les parties décimales chiffre
à chiffre à partir des dixièmes . |
|
Exemples : |
Comparons 37,23 et 8,9563 et
87,54 avec 87,45
On a 37,23 > 8,9563 (
car 37 > 8 )
On a 87,54 > 87,45 ( car
dans 87,54 ,le chiffre des dixièmes est plus grand que dans 87,45)
e) Ordonner des nombres
Définition : Ordonner
des nombres c’est les comparer entre eux
et les ranger dans un certain ordre.
On peut les ranger par ordre
croissant ( Exemple 1 ) ou par ordre
décroissant ( Exemple 2 ) .
Exemple 1 : 0,7 < 1
< 1,7 < 17,7
Exemple 2 :
17 > 7, 1 > 6,9
> 3,7
|
Activité : |
Comparer dans l’ordre
donné les nombres suivants :
0,56 et 0, 576 ; ……………………………………
97,087
et 97,086 ; ………………………………..
0,75 et
3/4 ; ………………………………………
corrigé à la fin du cours.
|
i9@ |
:iINFO plus@ |
a) « Encadrer »
un nombre par 2 autres nombres.
|
Définition : Encadrer un nombre c’est le placer entre un nombre plus petit que lui et un autre plus grand que lui . |
Exemple : Encadrement par deux nombres entiers
successifs :
« 7 est la valeur entière approchée par défaut »
7
< 7,6 < 8
« 8 est la valeur entière approchée par excès »
On dit que « 7 » est la valeur
entière approchée par défaut ; « 8 » est la valeur entière approchée par excès.
b) Encadrement d’un nombre entier :
-
b1) On peut encadrer un nombre ( entier ou décimal) par
deux nombres entiers :
73 < 89
< 134
73 est plus petit que 89 ; 134 est plus grand que 89
5 , 6 >
4 ,5 > 0
, 3 4
- b2)
On peut encadrer un nombre ( entier ou décimal ) par deux nombres entiers consécutifs .
*exemple : 3 ; 4 ; 5 ; 6 sont des nombres consécutifs :
par définition : on dira que
des nombres consécutifs sont des nombres qui se suivent à l’unité près .
exemples :
3 ;
4 ;
5
parce que ( 4 -1) ; 4 ; (
4 + 1)
et :
88 < 89 <
90
on remarque que « 8 8 » est immédiatement plus petit que
« 8 9 » et que « 90 » est immédiatement plus grand
que « 89 ».
c) Encadrement d’un « décimal »
·c 1 : par deux nombres décimaux quelconques :
Exemples : (qui n’ont qu’un chiffre après la virgule ).
6,7 < 6,95 <
7
7,8 > 6,9 >
3,6
· c 2 :Par deux nombres
décimaux successifs à une décimale ( 1 décimale signifie
qui n’a qu’un chiffre après la virgule ).
Exemple :
6,7 < 6,78
< 6,8
On dit que 6,7 est la valeur entière approchée à un
dixième par défaut ; 6,8 est la valeur entière approchée à un dixième par
excès.
· c3 : On peut encadrer par deux nombres
décimaux successifs à deux
décimales. ( 2 décimales signifie qui n’ont deux chiffres après la virgule).
Exemple : donner la
valeur approchée de 3, 872 9 au centième
près .
Pour le centième près , on
prend deux chiffres après la virgule .
3 , 87 < 3, 872 9 < 3,88
i on dit que 3,87 est la valeur approchée au
centième près par défaut ; 3,88
est la valeur approchée au centième près par excès.
d) Vocabulaire :
· Ordre
« croissant » :
Les nombres sont classés par
ordre « croissant » lorsqu’ils sont ordonnés du plus petit au plus
grand ,en partant de la gauche et en
allant de la gauche vers la droite .
Exemple : 3 ; 4,5 ; 7 ; 9 ;
14,5 on le note aussi : 3 <
4,5 < 7 < 9 < 14,5
· Ordre
« décroissant » :
Les nombres sont classés par
ordre « décroissant » lorsqu’ils sont ordonnés du plus grand au plus
petit , en partant de la gauche
et en allant de la gauche vers la droite .
Exemple : 14,5 ;
9 ; 7 ; 4,5 ; 3 ;
on le note : 14,5 >
9 > 7 > 4,5 >
3
On appelle une troncature le fait d’ignorer ou de « laisser tomber » des décimales de rang ou « ordre* donné » ; cet « ordre » ou « grandeur » étant suggéré ou imposé par l’exercice, le problème ou la situation , donnés.
*voir numération des nombres. @
|
Définition :On dit qu’un
nombre est tronqué à une « certaine » décimale ( à
un certain rang décimal demandé ) si les
valeurs décimales du ( ou des ) rang suivant
sont ignorées . |
Exemples :
3,14159 est la
valeur tronquée à 5 décimales de 3,141592254
3,1415 est
la valeur tronquée à 4 décimales de
3,141592254
3,141 est
la valeur tronquée à 3 décimales de 3,141592254
3,14 est
la valeur tronquée à 2 décimales de
3,141592254
3,1
est la valeur tronquée à 1 décimales de
3,141592254
3,
est la valeur tronquée à l’unité
d’unité de 3,141592254
iEn
informatique :
l’expression « troncature » est remplacée par l’expression « approximation
par défaut » @.
b) Arrondir un nombre à l’ « unité ». @
Définition : Arrondir un nombre à l’unité , c’est prendre le nombre entier le plus
proche de ce nombre .( on n’aura plus
aucun chiffre après la virgule .)
Exemple :
« l’arrondi à
l’unité » de 13,27 est 13 car
13,27 est plus proche de 13 que de 14 .
Règle :
-
si
le premier chiffre après la virgule est
0 ; 1 ;2 ;3 ;4 ; on prend la valeur entière par défaut
.(on ignore la valeur qui se trouve après la virgule)
-
si
le premier chiffre après la virgule
est 5 ; 6 ;7 ; 8 ;
9 ; on prend la valeur entière par excès . (on n’ignore pas la valeur qui
se trouve derrière la virgule)
c) Applications aux cas
courants (On peut de même, en transposant la règle
précédente J
¶ Arrondir un
nombre au dixième ( ou à une décimale)
Exemples :
· arrondir au
dixième 6,44 et 3,85 :
L’arrondi d’un nombre au dixième
de 6,44 est 6,4 ;
L’arrondi au dixième de 3,85 est 3,9
·L’arrondi d’une
longueur , au décimètre ( 0,1 m)
de 2,57 m
« L’arrondi au décimètre » de 2,57 m est
« 2,6 m » ; ( le décimètre est le dixième de mètre )
·L’arrondi à la dizaine
de centimes d’Euro , ( 0,1 €)
de 12,572 € est 12,6 €
· Arrondir un
nombre au centième ( ou à deux
décimales)
Exemples :
· L’arrondi d’un
nombre au centième de
6,443 est 6,44 ;
· L’arrondi au centième de 7,897 est 7,90
· L’arrondi au centime d’
Euro de 12,572 € est 12,57 € ; ( le centime est le centième
d’Euro )
· L’arrondi au
centimètre de 2,576 m est 2,58 m ;
( le centimètre est le centième de mètre )
¸ Arrondir un
nombre au millième ( ou à trois décimales)
Exemples :
· Arrondir au
centième 6,443 7 et 7,897 2
L’arrondi
d’un nombre au millième de
6,443 7 est 6,444 ; l’arrondi
au centième de 7,897 2 est 7,897
· L’arrondi au gramme de 5,789 6
kg
L’arrondi
au gramme 5,789 6 kg est 5,790
kg ; ( le gramme est le millième du kilogramme )
|
Règle de l’arrondi
à l’unité Arrondir un
nombre « à l’unité » c’est prendre le nombre entier le plus proche
de ce nombre en tenant compte de la valeur du premier chiffre après la virgule : -
Si
le premier chiffre après la virgule est
0 ;1 ; 2 ; 3 ; 4 ; (
les cinq premiers chiffres ) , on prend la valeur entière par défaut. -
Si
le premier chiffre après la virgule est
5 ; 6 ; 7 ; 8 ; 9 ; (
les cinq derniers chiffres) , on prend la valeur entière par excès. |
|
Règle d’arrondi à la décimale choisie ou imposée : Pour
arrondir un nombre à une décimale
imposée : -
On
tronque le nombre à droite de cette décimale . -
On s’interroge sur la valeur de la première
décimale que l’on supprime : si elle est supérieure ou égale à 5 on
ajoute « 1 » à la dernière décimale
écrite , sinon on garde la valeur tronquée du départ . |
Exemple :
Arrondir à deux décimales le nombre : 23 ,
4684
-
Troncature :
le nombre sera 23, 4 6(8),
-
le
(8)
est le chiffre qui doit disparaître .ce chiffre est supérieur à
« 4 » , on ajoute « 1 »
au « 6 » ; ( 6
+1 = 7 ) , 7 est le dernier chiffre retenu.
Ainsi :
arrondir à
deux chiffres décimales le nombre
« 23 , 4684 » donne
comme résultat : 23,47
 c) Vocabulaire
c) Vocabulaire
|
Les expressions suivantes sont équivalentes : |
Les
expressions suivantes sont équivalentes : |
Les expressions
suivantes sont équivalentes : |
|
- « Arrondir un nombre à une
décimale » . -
« Arrondir un nombre à
0,1 près » . » - « arrondir à un chiffre après la
virgule » - « arrondir à un rang décimal » |
- « Arrondir un nombre à deux décimales » -
« Arrondir un nombre à
0,01 près » - « arrondir à deux chiffres après la
virgule » » - « arrondir au deuxième rang décimal » |
- « Arrondir un nombre à trois décimales» -« Arrondir
un nombre à 0,001 près » -« arrondir à trois chiffres après la
virgule » -« arrondir au troisième rang décimal ». |
|
Cas
particuliers : ils feront l’objet
d’une étude particulière :
cliquer ici voir cours n°14 pour « l’aire » @
, et , cours n°19@ pour les volumes. |
Info +++ : les conversions d’aire. @ Info +++ : les conversions
de volume . @ |
ATTENTION :
LE TRAVAIL CI DESSOUS ne pourra être noté et validé que si les cours N°14 /25
et N° 19 /25 ont été étudiés et
validés.
EXERCICES : On demande d’ arrondir des résultats obtenus suite à un calcul et concernant les unités d’aires @ et des unités volumes @ .
Pour les aires :
l’unité principale est le « m² ».Exemple :donner un résultat
exprimé en m² et « arrondi »
au dm² il faudra 2 chiffres après la virgule ;si on veut
une résultat exprimé au cm² prés il faudra
4 chiffres ;et au mm² il faut 6
chiffres ! ! ! ! !
Voir avec les
volumes ! ! ! !
Pour les volumes si le résultat exprimé en m3 :
pour un résultat arrondi au dm3
il faudra 3 chiffres après la virgule ; au cm3 il faudra 6 chiffres après la virgule ; au
mm3 il faudra 9 chiffres
après la virgule ! ! ! ! !
Applications 1
1°) On a calculé et obtenu
les résultats suivants ; on demande
de les exprimer dans l’unité
donnée mais de les arrondir au
centimètre carré prés :
|
783, 4576589 m² |
® |
783,
4577 m² |
|
51,555674 dm² |
® |
|
|
128,699873452m ² |
® |
|
|
1 099, 73 cm² |
® |
|
2°) On a calculé et obtenu
les résultats suivants ; on demande
de les exprimer dans l’unité
donnée mais de les arrondir au décimètre
carré prés :
|
783, 4576589 m² |
® |
783,
46 m² |
|
51,555674 dm² |
® |
|
|
128,699873452m ² |
® |
|
|
® |
|
Applications 2
1°) On a calculé et obtenu les
résultats suivants ; on demande de
les exprimer dans l’unité donnée
mais de les arrondir au centimètre
cube prés :
|
783, 4576589 m3 |
® |
783,
457659 m3 |
|
51,555674 dm3 |
® |
|
|
128,699873452 m3 |
® |
|
|
1 099, 73 cm3 |
® |
|
2°) On a calculé et obtenu
les résultats suivants ; on demande
de les exprimer dans l’unité
donnée mais de les arrondir au décimètre
cube prés :
|
783, 4576589 m3 |
® |
783, 458 m3 |
|
51,555674 d m3 |
® |
|
|
128,699873452 m3 |
® |
|
|
1 099, 73 c m3 |
® |
|
Voir corrigé à la fin du
cours ! ! ! ! !
|
Exemples de problèmes
posés : |
|
A ) Un récipient
cylindrique utilisé pour une fondue bourguignonne a un diamètre intérieur de
15 cm et une hauteur de 12 cm. 1-
calculer,
en cm3 , son volume , arrondir
à l’unité. 2-
On
remplit ce récipient aux deux tiers avec une huile. Calculer en , cL, le
volume d’huile, arrondir à l’unité r |
|
B ) Une ménagère a besoin
d’un autocuiseur ayant une capacité de
10 litres. Cet autocuiseur
cylindrique à les dimensions intérieures suivantes : 24 cm de diamètre
et 17,7 cm de hauteur. 1- Calculer, en dm3
, le volume intérieur de l’autocuiseur , arrondir à l’unité. |
|
C )Arrondir au degré la
mesure d’un angle . |
|
D) A l’occasion de la fête
des mères , un magasin fait l’offre suivante : « l’ autocuiseur de
8 litres Offres spéciale 74 euros au lieu de 99 euros. » 1)
Calculer
le montant de la réduction en euros. 2)
Calculer
le pourcentage de réduction par
rapport au prix initial ; arrondir à 0,1. |
Corrigé des activités
1236,54
= 1 ![]() 1000 + 2
1000 + 2 ![]() 100+3
100+3 ![]() 10 + 1
10 + 1![]() 6 + 5
6 + 5 ![]() 0,1+ 4
0,1+ 4![]() 0,01
0,01
14
557, 354 = 10![]() 1000 + 4
1000 + 4 ![]() 1000 + 5
1000 + 5![]() 100+ 5
100+ 5 ![]() 10 + 7
10 + 7![]() 1 + 3
1 + 3 ![]() 0,1+ 5
0,1+ 5![]() 0,01+ 4
0,01+ 4![]() 0,001
0,001
14
788 ,708 =10![]() 1000 + 4
1000 + 4 ![]() 1000 + 7
1000 + 7![]() 100+ 8
100+ 8 ![]() 10 + 8
10 + 8![]() 1 + 7
1 + 7 ![]() 0,1+ 0
0,1+ 0![]() 0,01+ 8
0,01+ 8![]() 0,001
0,001
0,560
< 0, 576 ; ……
97,087
> 97,086 ; ………
0,75 = 3/4
; …
*
|
783,
4576589 m² |
® |
783,
4577 m² |
|
51,555674
dm² |
® |
51,56 dm² |
|
128,699873452m
² |
® |
128,699873
m ² |
|
1
099, 73 cm² |
® |
1
100 cm² |
*
|
783,
4576589 m² |
® |
783,
46 m² |
|
51,555674
dm² |
® |
52 dm² |
|
128,699873452m
² |
® |
128,70 m ² |
|
1
099, 73 cm² |
® |
1
1 dm² |
|
783,
4576589 m3 |
® |
783,
457659 m3 |
|
51,555674 dm3 |
® |
51,556
dm3 |
|
128,699873452
m3 |
® |
128,699873452
m3 |
|
1
099, 73 cm3 |
® |
1
100 cm3 |
2
|
783,
4576589 m3 |
® |
783,
458 m3 |
|
51,555674
d m3 |
® |
52
d m3 |
|
128,699873452
m3 |
® |
128,700 m3 |
|
1
099, 73 c m3 |
® |
Impossible :
on ne peut pas dans ce sens ; on ne peut pas garder le cm cube et exprimer en décimètre cube |
Demander
les documents pour l’auto- formation.
|
Leçon |
Titre |
|
N°1 |
@ LES TRAVAUX d ’ AUTO - FORMATION sur LES NOMBRES |
Consigne : il faut
répondre aux questions sur feuille ;
il faut rédiger les réponses.
PARTIE TRAVAUX
N°1 d ’ AUTO - FORMATIF :
CONTROLE
Questions relatives
au cours ; sur ce qu’il faut savoir.
PARTIE : TRAVAUX N°1
AUTO – FORMATIF : EVALUATION
Exercices relatifs
au cours ; sur ce qu’il faut savoir faire en niveau V.
Consigne : compléter les feuilles suivantes.
|
Série 1 )
Connaître l’ écriture décimale d’un nombre ; |
|
Consigne : Lorsque
votre travail personnel est terminé Vous devez consulter le corrigé soit sur le
site soit avec les documents « professeurs »

