CORRIGE des TRAVAUX
D’ AUTO - FORMATION N° 9 / 25 : EVALUATION: N°1
|
|
|
1° ) Donner deux suites de nombres proportionnelles :
exemple : {
2 ;3 ;4 ;5 ;}
et (je multiplie les nombres de
la suite par 3 ; d’où la 2ème suite { 6 ; 9 ; 12 ; 15 }
2°) Donner deux suites de nombres non
proportionnelles.
exemple : {
2 ;3 ;4 ;5 ;}
et (je multiplie que les 3
premiers nombres de la suite par 3 ;
d’où la 2ème suite { 6 ;
9 ; 12 ; 17 } ; « 17 »
est un nombre qui n’est plus en relation avec 5
{ 2 ;3 ;4 ;5 ;} et { 6 ; 9 ; 12 ; 17 } ne sont pas des suites de nombres
proportionnels
|
|
|
1°) Montrer que l’égalité des rapports forme une
proportion. ![]()
On calcule : 2 :4 = 0,5
et 6 :12 = 0,5
2°) que peut -on dire des produits
2 ![]() 12
et 4
12
et 4 ![]() 6
6
On remarquera que les multiplications 2 ![]() 12 et
4
12 et
4 ![]() 6
donne des produits égaux :
« 24 » .
6
donne des produits égaux :
« 24 » .
3°) Les fractions suivantes sont - elles équivalentes ? ![]() et
et ![]() ?
?
Solution :
« oui » si 3 fois 37,5 est égal à
15 fois 2,5 ;
Calcul
n°1: 3
fois 37,5 = 112,5 ; calcul n°2 15 fois 7,5 = 112,5
Conclusion :
on peut écrire que ![]() =
= ![]()
|
|
|
|
´
2 |
1,5 |
4,3 |
9,6 |
34,3 |
|
|
3 |
8,6 |
19,2 |
68,6 |
3 / 1 ,5 = 8,6 / 4,3 = 19,2 / 9,6 = 68,6 / 34,3 ;
le coefficient de proportionnalité est « 2 »
|
|
Problème I ) 2 kg de
pommes valent 1, 6 €, 3 kg valent 2,4 €, 5 kg valent 4 € .
1°) Montrer
qu’il y a proportionnalité.
On montre qu ‘il y a proportionnalité en effectuant les calculs (1,6 ¸2 ;
2,4 ¸
3 et 5 ¸
4) ; ce qui nous permet d’écrire la suite de nombres
« proportionnels » :
|
|
= 0,8
(0,8 étant le prix au kilogramme) |
On peut dire que le prix à payer est
égal à 0,8 € multiplié par le nombre de
kilogramme acheté.
2°) Etablir une formule, où « y » le prix à
payer sera obtenu en fonction de « x » ( noté : f ( x)
) , où « x » désigne le nombre de kilogrammes achetés.
Si on désigne par « y » le prix à
payer ; par « x » le nombre de kilogramme acheté on peut
écrire la formule : y = 0,8 x
ou f(x) = 0,8 x
Problème N°2 :
1°) Le prix d’un kg de fruit est de 1,2 €. Donner une
formule permettant de calculer le prix à payer en fonction de la masse achetée.
Solution
Pour tout achat de ces fruits, on a :
prix à
payer =
prix au kg ![]() nombre
de kg
nombre
de kg
Si on appelle « x » le nombre de
kg achetés et « y » le prix à
payer on écrira :
y =
1,2 x
Problème N°3 : Des
pommes sont vendues à 1,53 € le
kilogramme.
A) quelle sera la relation mathématique à utiliser ?
B) quelle est la somme à payer si l’on
prend 4,5 kg , et 1,350 kg.
Solution :
A) si « y » est le prix à payer
et « x » le nombre de kg , 1,53 est le coefficient de proportionnalité . je
dois payer : y = 1,53 x
B)
-si je prend 4,5 kg
; je payerai y = 1,53 fois 4,5 ; soit 6,885 €
-si je prend 1, 350 kg ; je payerai y = 1,53 fois 1,350
; soit 2,0655 €
problème n°4 : J’ai payé
7,2 € pour des pommes vendues 0,8
€ au kg . Quelle est la masse de pommes achetées ? ( donner 2 façons de
procéder )
Solution 1 : On
sait que la relation à utiliser
est y = 0,8 x
On connaît « y = 7,2 » , on peut écrire 7,2 =
0,8 x
|
Pour calculer « x » on
transforme l’équation : |
|
On simplifie pour obtenir : ![]()
Donc
x = 7,2 ¸ 0,8
; soit x =
9
conclusion : la masse de pommes achetées est de 9 kg.
Autre méthode de résolution d’un problème
sur les proportionnalités : on
raisonne en passant par le tableau de proportionnalité.
Problème :
J’ai payé 7,2 € pour 10 kg pommes combien paierai-je pour 4
kg ?
solution : (on établit le tableau suivant)
|
Nombre
de kg |
10 |
4 |
|
Prix
payé |
7,2 |
( x ) |
Calcul : On fera le produit en croix :
10 ´
( x ) = 7,2 ´ 4
; on transforme : ( x) =
( 7,2 ´ 4
) ¸
10 ; x = 2,88
Conclusion :
le prix à payer pour 4 kg est de 2,88 €.
|
|
Problème N° 1 :
Des pommes
sont vendues 2 € au kg.
1°) Combien
paierai-je si j’ achète une
masse ( notée par la lettre « x » ) de pommes
achetées ? (On demande d ’ établir
l’équation)
2°) Construire un tableau ou l’on peut connaître les
prix à payer pour des sacs contenant 1,5 ; 2 ;
2,5 ; 3 ; 4 et 5 ( kilos achetés).
Solution :
1°) On pose : « x » pour les kilos achetés ; « y »
pour le prix à payer ; On en déduit
l’équation « y = 2 x »
2°) On en construit le tableau de proportionnalité :
|
|
x |
1,5 |
2 |
2,5 |
3 |
4 |
5 |
|
|
y |
3 |
4 |
5 |
6 |
8 |
10 |
|
|
Problème : J’achète 9 kg
de pommes pour 7,2 € ; une offre
promotionnelle propose un lot de 3 kg de ces mêmes pommes à 2,99 €.
Y a - t-il un rapport de
proportionnalité ?
Solution :
Pour le savoir on effectuera les deux calculs suivants
( 7,2 : 9
et 2,55 : 3 ) et puis on
comparera le résultat de ces calculs
: 7,2 : 9 = 0,8 ; 2,55 : 3 = 0,85 ;
0,8
et 0,85 ne sont pas égaux !
Conclusion : Il
n’y a pas de proportionnalité parce que l’on a pas obtenu le même quotient.
|
|
Problème N° 1 : Un cycliste se
déplace à la vitesse moyenne de 20 km par heure ( 20
km/h ou 20 km.h-1 ).
A) Déterminer
l’équation « y » distance parcourue(km)
en fonction de « x » durée du parcours(h) ;
B) construire un tableau de proportionnalité avec x = 1 h
; 2h et 3
h ;
C) Tracer la droite
dans un repère cartésien.
Solution :
A) L'équation
algébrique est y = 20 x
Avec " y
" la distance parcourue, "x"
la durée en heure.
B) tableau :
|
Points ® |
A |
B |
C |
|
Durée en h. |
1 |
2 |
3 |
|
Distance
parcourue |
20 |
40 |
60 |
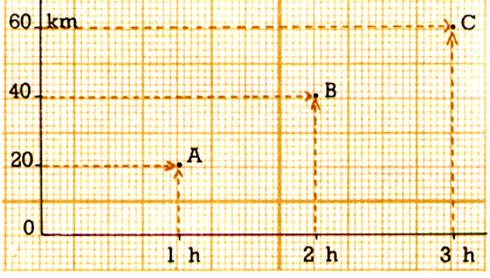
C) On trace le repère ( sur « x » 1h = 2
cm ; sur « y » 20 km = 1
cm )et puis on place les points A ( 1 ;
20) ; B ( 2 ; 40 ) ; C ( 3;60 )
|
La
représentation graphique est une droite |
|
Rechercher un complément d'informations à la lecture de la représentation graphique, et interpréter certains
événements :
|
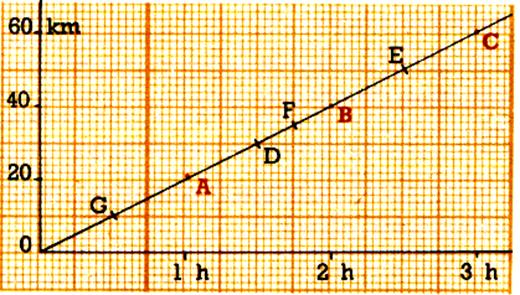
Soit la représentation graphique ci- contre. « Soit un cycliste qui quitte un lieu en un
point O » . |
|
1°) Compléter le tableau ci - dessous :
|
|
? |
G |
? |
D |
F |
? |
E |
? |
|
Durée en h. |
0 |
0,5 |
1 |
|
1,75 |
2 |
|
3 |
|
Distance parcourue |
0 |
|
20 |
30 |
|
40 |
50 |
60 |
2°) Quel commentaire peut -
on faire sur les
points : G : D ; F et E ?.
Solution :a) Après avoir remplir le tableau :
|
|
O |
G |
A |
D |
F |
B |
E |
C |
|
Durée en h. |
0 |
0,5 |
1 |
1,30 |
1,75 |
2 |
2,50 |
3 |
|
Distanceparcourue |
0 |
10 |
20 |
30 |
35 |
40 |
50 |
60 |
b) On peut faire les commentaires suivants :
au point
"G" il met 0,5h pour parcourir 10 km
au point
"D" il parcourt 30 km en 1,5 h
au point
"F" en 1,75 h ( 1 .![]() h ou 1 h 45 min) il a
parcouru 30 km
h ou 1 h 45 min) il a
parcouru 30 km
au point
"E" il a parcouru 50 km au
bout de 2,5 h ( 2h 30 mn )
|
IX) Application linéaire . |
|
1°) Application linéaire :
· « k » est un nombre non nul ( ¹ 0)
· L’application linéaire de
coefficient « k » fait correspondre à chaque nombre « x »
le nombre « k ´ x ».
on notera le calcul de k ´ x = y soit
y = k x ,
où on dira
que le produit de « k x » est l’image de « x » par l’application linéaire
de coefficient « k » . On dira donc
que « x à pour image k x »
« x à
pour image k x » : on
notera cette phrase par l’écriture symbolique : x ![]() k x
k x
· Si l’application linéaire
s’appelle « f » et si « y » est l’image de
« x »
on
notera
2°) Application linéaire liée à
une situation de proportionnalité .
soit : y = f (x)
on pose : x ![]() -3,5
x
-3,5
x
compléter le tableau ci -dessous :
|
´ -3,5¯ |
x |
- 3 |
- |
0 |
0,4 |
1 |
2 |
|
y |
+10,5 |
+1 |
0 |
-1,4 |
-3,5 |
-7 |
3°) faire la représentation graphique de l’ équation : y = - 3,5 x
Elle passe par le point
« O » ( 0 ;
__ ) et par
le point « A » ( 1 ; ___
)
Calcul d’un Coefficient :
On donne l’application linéaire f
telle que f ( 2)
= ( -13) ; justifier .
à pour coefficient ![]() car
car ![]()
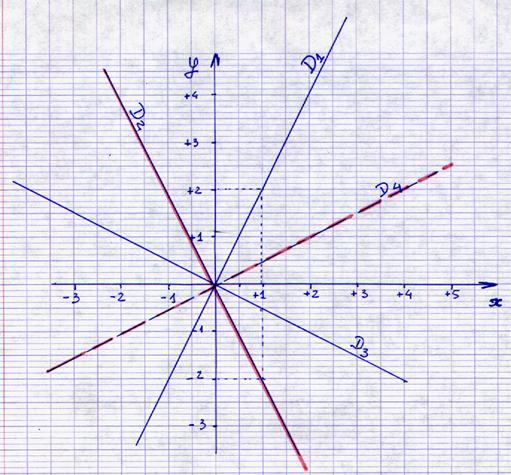
5°) Dans les représentations graphiques
des droites passant par « O » suivantes :
Retrouver le coefficient directeur de
chacune des droites D1 ; D2 ; D3 ; D4
Pour se faire on
recherchera : sachant que a = y / x
et si x =1 alors a = y /1 donc
on en déduit que a = y = k.
D1 = ;
pour x = 1 alors y = +2 ;
donc k = 2
D2 =
; pour x = 1 alors y =
-2 ; donc k = -2
D3 =
; pour x = 1 alors y =
- 0,5 ; donc k = -0,5
D4 = ;
pour x = 1 alors y = + 0,5 ; donc k = 0,5
|
La
représentation graphique d’une fonction linéaire est une droite passant par
« O ». D1 ; D2 ; D3 ;
D4 sont des droites
passant par « O » |
|
TRAVAUX D’ AUTO - FORMATION N° 9 / 25 : EVALUATION:
N°2
|
|
Corriger
cliquer ici :EVALUATION:
N°2 |
I )
Sur les suites :
1°) Les deux
suites de nombres 4 ; 6 ; 16 et 14 ; 21
; 56 sont-elles proportionnelles ?
Justifier la réponse en écrivant les opérations.
2°) Les deux suites de nombres 12 ; 13 ; 14 ;15; 16 et 24 ; 26
;28 ; 30 ; 32 sont-elles
proportionnelles ?
Justifier la réponse en écrivant les opérations.
II )
Les tableaux :
1°) mettre les suites suivantes proportionnelles :
12 ; 13 ; 14 ;15; 16
et 24 ; 26 ;28 ; 30 ; 32 dans un
tableau à double entrée . ( les "x" pour la
première suite et les "y" pour la deuxième suite ).
2°) Le tableau suivant donne le montant de différents achats de fuel . Y a - t - il
proportionnalité ? Si oui calculer le coefficient de proportionnalité
.
|
Quantité
en litres (x) |
32 |
35 |
40 |
48 |
55 |
|
Prix
en € (y) |
20,640 |
22,575 |
25,8 |
30,96 |
|
3°)le tableau suivant
donne le prix à payé en euro pour acheter des cahiers . Y - a
- t -il proportionnalité ? si oui , calculer le coefficient .
|
Nombre
de cahiers |
5 |
8 |
20 |
40 |
50 |
|
Prix
en € |
7,50 |
10 |
18 |
30 |
50 |
4°) Compléter le tableau suivant : il y a
proportionnalité !
|
Nombre
de cahiers |
5 |
8 |
|
|
50 |
|
Prix
en € |
7,50 |
|
18 |
30 |
|
5°) On donne le tableau suivant :
|
|
O |
A |
B |
C |
D |
E |
F |
G |
|
"x" |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
y |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
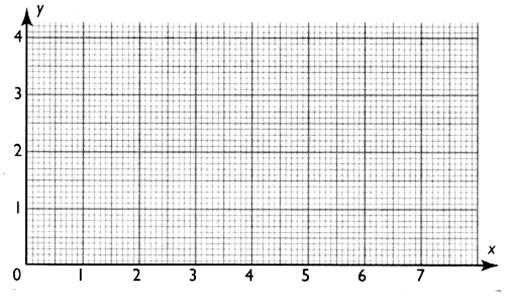
Pour
chaque couple de nombre ( x ; y ) ,
correspond les coordonnées d'un point . exemple: au point A
on associe l'abscisse x = 1 et l'ordonnée y = 0,5 ;
Placer le point A et tous les autres points de O à
G ; dans le repère ci dessous.
|
|
( on ne demande pas de tracer une droite)
III
)
Produit en croix :
Calculer "x" dans les proportions
suivantes:
|
|
Réponses : |
|
|
|
|
|
|
|
|
|
|
|
|
IV)
Problèmes de situations algébriques :
L'expression algébrique permettant de calculer une grandeur
"y" en fonction d'une autre grandeur "x" est y
= 0,5 x .
1°) Compléter le tableau ci dessous :
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
y |
|
|
|
|
|
|
|
|
2°) chaque couple de nombres ( x
; y ) , nommer chaque colonne par une
lettre majuscule , placer le point correspondant dans le repère ci dessous et
tracer la droite représentant la situation.
|
|
V ) Situations Problèmes
vie quotidienne N°1..
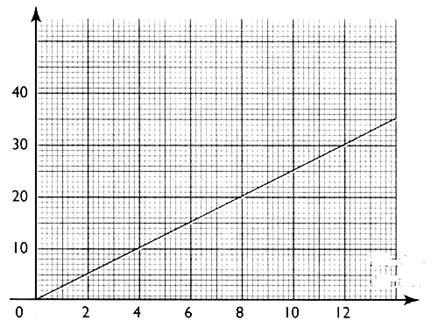
Le graphique ci dessous représente le prix à payer
en euros en fonction du nombre de kilogrammes de pomme de terre achetée.(nommer les
axes : Kg et €)
|
|
a) Compléter
le tableau de proportionnalité :
|
Nombre de Kg |
0 |
1 |
2 |
4 |
6 |
8 |
10 |
12 |
|
Prix en € |
|
|
|
|
|
|
|
|
b )
Calculer le coefficient de proportionnalité .
c )
Ecrire l'expression algébrique correspondant à cette situation .
Vie
quotidienne N°2..
Sur une
photo un enfant mesure 4 cm et le
père 5 cm . la taille réelle du père est de 1,75 m .
a) Compléter le tableau :
|
|
Enfant |
Père |
|
Mesures de la photo en cm |
|
|
|
Mesures réelles en mètres |
|
|
b)calculer le
coefficient de proportionnalité. :
a)
calculer la taille réelle
de l'enfant .
|
De nombreux problèmes sont proposés dans le cours
suivant . |
TESTS :
Entourer la bonne réponse :
|
1.
Sur une carte à l’échelle Ses
dimensions réelles sont : |
1ère réponse |
12 m ´ 6m |
|
|
2ème réponse |
7,5 m ´
10 m |
|
|
|
3ème réponse |
75 m ´ 100 m |
|
|
2. Un rôti de 1,2 kg coûte 18 € . Un rôti de 1,750 kg
coûterait : |
1ère réponse |
22,5
€ |
|
|
2ème réponse |
28,90
€ |
|
|
|
3ème réponse |
26,25
€ |
|
|
3. Un
piéton a mis 2h15 m n pour parcourir 9 km .A la même vitesse , pour parcourir il mettrait : |
1ère réponse |
60
min |
|
2ème réponse |
1h
24 min |
|
|
3ème réponse |
56
min |
Déterminer et
représenter les situations de
proportionnalité.
|
|
x |
y |
y
= ….´ x |
|
1°)
situation |
|
|
|
|
2°)
situation |
|
|
|
|
3°)
situation |
|
|
|