DOSSIER : N°9: CORRIGE : La proportionnalité et les calculs sur la proportionnalité et
L’application linéaire
1°) Deux suites de nombres forme une
suite de nombres proportionnels
si …le rapport…………….
entre les nombres de la première suite et les nombres correspondants de la
deuxième est ……constant……………… .
2°) L'égalité de deux rapports est appelée "…proportion……………..." .
3°) Que faut-il « avoir comme nombres » pour
calculer le : "produit en
croix" : Pour pouvoir faire le produit en
croix il faut être en présence de l’égalité de deux fractions .
4°) Compléter la phrase : dans une proportion le produit …des extrêmes…. est égal au produit ……………des moyens ……… .
5°) Calcul du coefficient de
proportionnalité :
Le coefficient de
proportionnalité est égal au rapport des nombres de la
deuxième suite aux nombres correspondants de la première suite
6°) Comment appelle - t- on cette équation
« y = ax » ? est appelée : « équation de la fonction
linéaire » .
7°) Quel lien y a - t- il entre la proportionnalité et la fonction
linéaire .
la fonction linéaire est le modèle algébrique permettant de traiter toutes les situations problèmes
de la proportionnalité.
8°) construire un tableau de proportionnalité .
Procédure : On construit deux
lignes « x » et
« y » et autant de colonnes que de valeurs cherchées.
On remplit la ligne des « y ».
|
|
x |
|
Dans cette Ligne
supérieure les nombres forment la
« Première suite ». Les valeurs de « x » sont
données ou choisies . |
|
|
|
|
y |
|
Dans cette Ligne
inférieure les nombres forment la
« seconde suite », les valeurs de « y » sont
calculées .on sait que les valeurs de
« y = ax » |
|
|
Sur les suites :
1°) Les deux
suites de nombres 4 ; 6 ; 16 et 14 ; 21
; 56 sont-elles proportionnelles ?
Justifier la réponse en écrivant les opérations.
Oui si elles forment une suite de
rapports égaux et
si 14 /4 = 21/6 = 56 /16
Ce qui est le cas ! ! !
parce que 14 /4 = 21/6 = 56 /16 = 3,5
2°) Les deux suites de nombres 12 ; 13 ; 14 ;15;
16 et 24 ; 26 ;28 ; 30 ; 32 sont-elles proportionnelles ?
Justifier la réponse en écrivant les opérations.
Oui si elles forment une suite de
rapports égaux .
Parce que 24 :12 = 26 : 13 = 28 : 14 = 30 : 15 =
32 : 16
Les
tableaux :
1°) mettre les suites suivantes proportionnelles :
12 ; 13 ; 14 ;15; 16 et 24 ; 26 ;28 ;
30 ; 32 dans un tableau à double entrée
. ( les "x" pour la première suite et les "y" pour la
deuxième suite ).
|
x |
12 |
13 |
14 |
15 |
16 |
|
y |
24 |
26 |
28 |
30 |
32 |
2°) Le tableau suivant donne le montant de différents achats de fuel . Y
a - t - il proportionnalité ? Si oui calculer le coefficient de proportionnalité
.
|
Quantité
en litres (x) |
32 |
35 |
40 |
48 |
55 |
|
Prix
en € (y) |
20,640 |
22,575 |
25,8 |
30,96 |
|
20 , 640 : 32 = 0,645 ;
22,575 : 35 = 0,645 ; 25,8 : 40=
0,645 ;30,96 : 48 = 0,645
conclusion :il y a proportionnalité
entre les deux suites ; le coefficient est 0,645.
3°)le tableau suivant donne le prix à payé en euro
pour acheter des cahiers . Y - a - t -il
proportionnalité ? si oui , calculer le coefficient .
|
Nombre
de cahiers |
5 |
8 |
20 |
40 |
50 |
|
Prix
en € |
7,50 |
10 |
18 |
30 |
50 |
|
Recherche si K ? |
1,5 |
1,25 |
0,9 |
0,75 |
1 |
conclusion :il n’y a pas « proportionnalité » entre les deux
suites ; puisque nous n’avons pas de valeur commune « k » .
4°) Compléter le tableau suivant : il y a
proportionnalité !
calcul de k = 7,5 : 5 =
1,5
|
Nombre
de cahiers |
5 |
8 |
12 |
20 |
50 |
|
Prix
en € |
7,50 |
12 |
18 |
30 |
75 |
5°) On donne le tableau suivant :
|
|
O |
A |
B |
C |
D |
E |
F |
G |
|
"x" |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
y |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
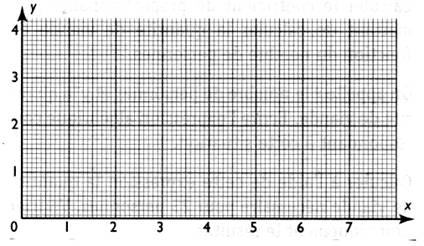
Pour
chaque couple de nombre ( x ; y ) , correspond
les coordonnées d'un point . exemple:
au point A on associe l'abscisse x = 1 et l'ordonnée y = 0,5 ;
Placer le point A et tous les autres points de O à
G ; dans le repère ci dessous.
|
|
( on ne
demande pas de tracer une droite)
Produit
en croix :
Calculer "x" dans les proportions
suivantes:
|
|
"x" = 600 : 15 = 40 |
|
|
|
|
|
"x" = (24 fois 39) : 104 |
|
|
|
|
|
"x" = (50 fois 16): 20 |
|
|
|
|
|
"x" = (2,5 fois 8) : 5,2 |
Problème
situation algébrique :
L'expression algébrique permettant de calculer une grandeur
"y" en fonction d'une autre grandeur "x" est y
= 0,5 x .
1°) Compléter le tableau ci dessous :
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
y |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
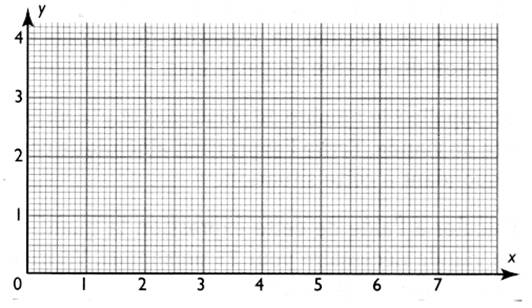
2°) chaque couple de nombres ( x ; y ) , nommer chaque colonne par une lettre
majuscule , placer le point correspondant dans le repère ci dessous et tracer
la droite représentant la situation.
|
|
Situation
Problème vie quotidienne N°1..
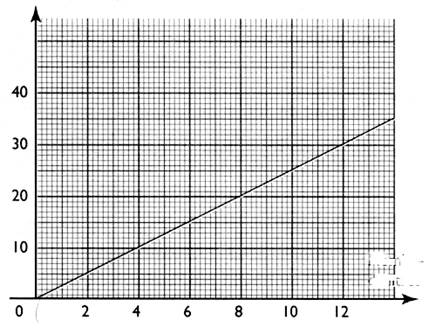
Le graphique ci dessous représente le prix à payer
en euros en fonction du nombre de kilogrammes de pomme de terre achetée.(nommer les axes : Kg et €)
|
|
a) Compléter
le tableau de proportionnalité :
|
Nombre de Kg |
0 |
1 |
2 |
4 |
6 |
8 |
10 |
12 |
|
Prix en € |
|
|
|
|
|
20 |
|
|
b ) Calculer le coefficient de proportionnalité
. 20 :8 =
2,5
c ) Ecrire l'expression algébrique correspondant à
cette situation . y = 2,5 x
Situation
Problème vie quotidienne N°2..
Sur une
photo un enfant mesure 4 cm et le
père 5 cm . la taille réelle du père est
de 1,75 m .
a) Compléter le tableau :
|
|
Enfant |
Père |
|
Mesures de la photo en cm |
4 |
5 |
|
Mesures réelles en mètres |
|
175 |
b)calculer le coefficient de
proportionnalité. : 175 : 5 = 35
a)
calculer la taille réelle
de l'enfant . 35
fois 4 = 140 cm
TESTS :
Entourer la bonne réponse :
|
1.
Sur une carte à l’échelle
Ses
dimensions réelles sont : |
1ère réponse |
12 m ´ 6m |
|
|
2ème réponse |
7,5 m ´
10 m |
|
|
|
3ème réponse |
75 m ´ 100 m |
|
|
2. Un rôti de 1,2 kg coûte 18 €
. Un rôti de 1,750 kg coûterait : |
1ère réponse |
22,5
€ |
|
|
2ème réponse |
28,90
€ |
|
|
|
3ème réponse |
26,25 € |
|
|
3. Un
piéton a mis 2h15 mn pour parcourir 9 km .A la même vitesse , pour
parcourir 4 km il mettrait : |
1ère réponse |
60 mn |
|
2ème réponse |
1h
24 mn |
|
|
3ème réponse |
56
mn |
Déterminer et
représenter les situations de
proportionnalité.
|
|
x |
y |
y
= a. x |
|
1°)situation |
3 |
750 |
y = |
|
2°)
situation |
1,2 |
18 |
y = 18 x |
|
3°)
situation |
9 |
135 |
y = 15 x |