|
TRAVAUX D’ AUTO FORMATION CONTROLE Série 1 |
|
|
N°9 |
LA PROPORTIONNALITE et les calculs sur la
proportionnalité ;son
l’application linéaire . |
|
|
VOCABULAIRE :
a) Rapport :
Compléter la
phrase :
On appelle « rapport » est le ………………………obtenu par la division d’un nombre par un
autre nombre.
Compléter la phrase :
Le modèle mathématique d’un « rapport »
est « ……………………………………………. ».
Quelle est la forme
du quotient ?
b) Rapports égaux :
Compléter
la phrase : On appelle « rapports égaux » des divisions qui ont ……………………………………………………………………………………………………
- Compléter la phrase : Le modèle mathématique
de deux rapports égaux est …………………………………………………………………………………………………...
- Donner le
modèle mathématique : ………………………………………………………..
c) Suite de rapports égaux :
1°) Compléter la phrase : Lorsque nous avons plus de deux rapports
égaux nous pouvons dire que nous
avons une « ……………………………… » , le quotient de chaque rapport étant ………………………, c’est un nombre dit « …………… » appelé « ………. ».
2°) Donner la traduction
en langage mathématique :
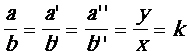
|
|
1° ) Donner la
définition d’ une suite proportionnels :
2°) Donner la procédure permettant de vérifier si
deux suites de nombres forment une suite de nombres proportionnels.
|
|
1°) Donner la définition
d’une proportion :
2°) Soit l’égalité : ![]() , donner un nom à cette égalité. :
, donner un nom à cette égalité. :
3°) Soit l’égalité : ![]() : que peut - on
dire des produits a
: que peut - on
dire des produits a ![]() d
et c
d
et c ![]() b
b
4°) Comment
appellent -on ces
produits : a ![]() d
et c
d
et c ![]() b ?
b ?
4°) Dans la proportion ![]() ;dont on veut
appliquer le produit en croix , comment appelle- t - on
les lettres représentant les
nombres « a » et
« d » et les nombres
« b » et « c » ?
;dont on veut
appliquer le produit en croix , comment appelle- t - on
les lettres représentant les
nombres « a » et
« d » et les nombres
« b » et « c » ?
5°) Compléter la phrase
suivante :
Dans une proportion le produit des.
6°) On dit
que dans une proportion les deux fractions sont équivalentes.
Comment peut-on vérifier si les deux fractions sont
équivalentes ?
7°) A quelle condition peut -on dire que les
fractions suivantes ![]() sont - elles équivalentes ?
sont - elles équivalentes ?
1°) Compléter la
phrase : Le coefficient de
proportionnalité est ……………...
2°) Quand dit - on
que le coefficient de proportionnalité existe ?
|
|
¯ |
1,5 |
4,3 |
9,6 |
Donner le nom de cette
première ligne : Dans cette
Ligne supérieure les nombres forment la « …………………… » |
¸
……. |
|
3 |
8,6 |
19,2 |
Donner le nom de cette
ligne : Dans cette Ligne
inférieure les nombres forment la
« ………………………….. » |
Vérifications : On a bien 4,3 ![]() 2 =
8,6 et 9,6
2 =
8,6 et 9,6![]() 2 = 19,2
2 = 19,2
3°)
a quoi est égale le coefficient de
proportionnalité
|
|
La fonction linéaire est le
modèle algébrique permettant de
traiter toutes les situations problèmes de la
………………………..
|
|
Compléter tableau
de proportionnalité : soit « a » le coefficient de
proportionnalité ;
|
|
x |
x1 |
x2 |
………. |
x4 |
x5 |
…….. |
|
|
y |
………. |
………. |
ax3 |
……… |
……… |
ax6 |
|
|
Soit
le tableau de proportionnalité , montrer
comment on obtient le coefficient de proportionnalité :
|
x |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|
y |
ax1 |
ax2 |
ax3 |
ax4 |
ax5 |
ax6 |
On effectuera les calculs
suivants :
|
|
1°) Quelle est la
représentation graphique d’une situation de proportionnalité ?
|
|
:
· « k » est un nombre ……………
( ou
on dit aussi : …………………………….)
· L’application linéaire de coefficient « k » fait correspondre
à chaque nombre « x » le nombre
« ……………… ».
on notera le calcul
de k ´ x
= y soit l’équation :
où on dira
que le produit de « k x » est l’image
de « x » par l’application linéaire de coefficient
« k » . On dira donc que « x à pour image k x »
« x à
pour image k x » : on notera
cette phrase par l’écriture symbolique :
……………………
· Si l’application linéaire s’appelle « f » et si
« y » est l’image de « x »
on notera
……………………….
2°) Application linéaire
liée à une situation de proportionnalité. :
On donne : x ![]() a x ;
compléter le tableau de proportionnalité
a x ;
compléter le tableau de proportionnalité
|
« …… » |
x |
x1 |
x2 |
……… |
x4 |
x5 |
……. |
|
y |
…….. |
…….. |
ax3 |
…….. |
…….. |
ax6 |
3°) Représentation
graphique
Compléter la phrase :
La représentation graphique de l’application linéaire de coefficient
« k » est la ………….. d’équation ………………..
Elle passe par deux points remarquables, lesquels ?
Elle passe
par le point ………………… et par le point …………………
4°) Coefficient :
Soit l’application linéaire f telle que
f ( x1) = ( y1)
, donner le calcul permettant d’obtenir
le coefficient ……………………
5°) Exemple de
représentations graphiques :
|
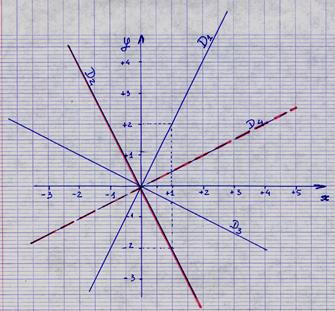
La représentation graphique d’une fonction
linéaire est une droite passant par « O ». D1
; D2 ; D3 ; D4 sont des droites passant par
« O » Quel est le signe du coefficient ? D1 = …….. ; D2 = ……. ; D3 = ……. ; D4 = ………… |
|