@

Leçon

Titre

N°18

CORRIGE - LES  POLYGONES  USUELS

CONTROLE:

1°) donner la définition d’un polygone régulier .Par définition : Un polygone est dit « régulier » lorsque tous ses cotés sont égaux ainsi que  tous ses angles.

2°) donner le nom des 8 polygones usuels .

le triangle isocèle , le triangle équilatéral  , le triangle rectangle , le trapèze , le parallélogramme , le losange , le rectangle , le  carré .

 

3°) nommer les  cinq principaux  polygones réguliers ( combien ont - ils de côtés ) ?

1)     Le triangle équilatéral

3 cotés

2)     Le carré

4 cotés

3)     Le pentagone régulier

5 cotés

4)     L’hexagone régulier

6 cotés

5)     L ‘ octogone régulier

8 cotés

4°) Nommer  et donner les propriétés des polygones usuels.

 

Description

Propriétés. ( pour en savoir plus sue les propriétés et les caractéristiques des figures , cliquer sur Cd :info plus )

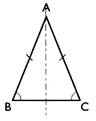
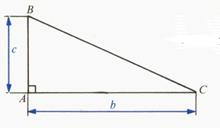
Triangle isocèle (ACB)

-         Deux côtés de même longueur : [ A B]  et [AC]

-         Deux angles de même mesure :   et

-         Un axe de symétrie : la médiatrice  du coté [BC]

Triangle équilatéral  (ACB)

-         trois côtés de même longueur: [ A B]  , [AC]  et [B C]

-         Trois angles égaux :  ,   et

-         Trois axes de symétrie .ce sont  les supports des trois médiatrices des côtés.

 

Triangle rectangle .(BAC)

 

- possède un angle droit .le milieu de l'hypoténuse est le centre du cercle circonscrit.(point de convergence des médiatrices ) .

Trapèze: ( ADCB)

-         deux côtés parallèles : [ A D]  , [BC]

-         deux côtés non parallèles : [ A B]  , [DC]

 

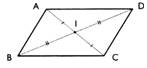
Parallélogramme :

( ADCB)

-         Côtés sont parallèles et égaux deux à deux .

-         Les diagonales se coupent en leur milieu .

-    Dans un parallélogramme les angles opposés sont égaux.

 

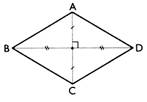
Losange : ( ADCB)

-         Côtés parallèles deux à deux et de même longueur.

AD = DC =C B = BA

-    Les diagonales sont perpendiculaires : [ A C]  , [BD] .

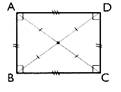
Rectangle (ADCB)

-         parallélogramme ayant quatre angles droits.

-         Les diagonales sont de même longueur .

 

Carré : ( ADCB)

-         parallélogramme ayant quatre angles droits et dont les diagonales , de même longueur , sont perpendiculaires.

-         Rectangle dont deux côtés consécutifs ont même longueur .

-         Losange ayant un angle droit .

 

 

5°) Calculs :

Compléter la phrase :

Pour les calculs les unités de longueurs doivent être homogénéisées  . ( à savoir : toutes les longueurs doivent être exprimées dans la même unité)

6°)  Donner les formules  permettant de calculer  l’aire de chacune des figures suivantes :

 

Intitulés

Formules

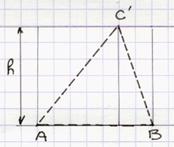
Aire du triangle quelconque ( scalène):

Aire =

Ou

Aire =   

b : longueur de la base.

h : longueur de la hauteur.

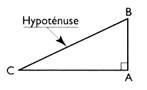
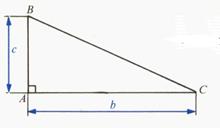
Aire  du triangle rectangle :

Aire =

Aire du triangle isocèle  :

Aire =

 

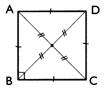
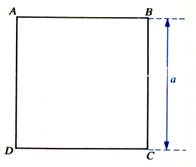
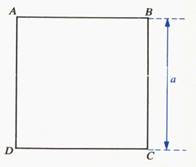
Aire du carré :

Si "a" est la mesure du côté .

Aire :

 A  = a²

Avec  "a"  : longueur du côté

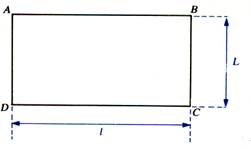
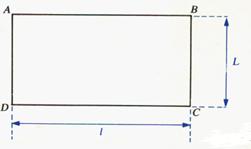
Aire du rectangle :

Aire :     A =  L  l

L : longueur

l : largeur

 

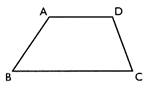
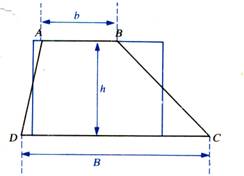
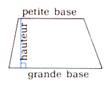
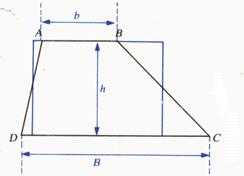
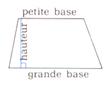
Aire du trapèze :

 

Aire : A =

B : longueur de la grande base.

b:  longueur de la petite base.

h  : hauteur

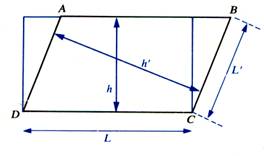
Aire du parallélogramme :

Aire :     A =  L  h

L : longueur

h : hauteur

ou

A =  L'  h'

 

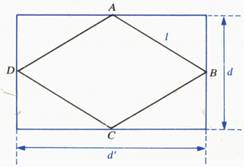
Aire du losange :

Aire : A =

 d ' : grande diagonale.

 d :   petite diagonale .

 

 

EVALUATION:   

Série 1  "Tests" reprise des exercices "cour"

 

Exemples de calculs d’aires:

 

 

1°) calculer l'aire du triangle  avec  b = 20 cm et h = 13 cm

solution : A =      ;  A  =   ; A = 130 cm²

 

2°) Calculer l'aire du carré  dont la longueur du carré est de  110 mm.

Solution : A = 110   110 ;    A = 12100 mm²

 

 

3°) Calculer l'aire du rectangle   dont la longueur est de  110 mm et la largeur est de 7 cm . ( exprimer le résultat en cm²)

Solution :   L = 110 mm = 11 cm ; l = 7 cm

 A = 11   7 ;    A = 77 cm²

 

4°) Calculer l'aire du trapèze   dont la grande base est de  11 cm et la petite base est de 9 cm et la hauteur est de 6 cm. ( exprimer le résultat en cm²)

Solution :   A =    ;    A  =   =  60 cm²

Série 2:

1°) Un rectangle a pour dimensions 1 , 06 m et 0,74 m .

Calculer son aire ( aire = longueur  largeur ) et l' exprimer en m² et en cm² .

106  cm fois 74 cm  = 7844   cm²

2°)   Un rectangle  a pour dimensions  83 cm et 167 mm.

Calculer son aire ( aire = longueur  largeur ) et l' exprimer en m² et en cm²  et mm².

13861  mm²  =  138,61 cm²  = 0, 013861 m²

 

 

 

 

 

 

 

 

 

Intitulés

Données :

 

Aire du triangle quelconque ( scalène):

AB = 20  cm

H =  80 mm  

 

A = (20 fois 8) /2 =

    ( 160 cm²) /2 = 80 cm²

 

 

Aire  du triangle rectangle :

   b =  150 mm

   c = 1 dm

A =  (150 fois 100)/2 =

15000 mm²/ 2  =

75 000mm²

 

Aire du triangle isocèle  :

  a =  12 cm

 

(12 fois 12  )/ 2=

( 144 ) / 2 = 72 cm²

 

 

Aire du carré :

Si "a" est la mesure du côté .

   a  =  8,5 dm

A = 8,5 dm fois 8,5 dm

A = 72,25 dm²

 

Aire du rectangle :

L : =  7,8 cm

l : =   52 mm

78 fois 52 = 4056  mm²

 

Aire du trapèze :

 

 

B : = 35 mm

b:  = 20 mm

h  : = 1,7 cm

 

[ ( 35 + 20) 17] /2 = A

A = 467,5 mm²

 

 

Aire du parallélogramme :

L =  34 cm

h :    18,9 cm

34 cm fois 18,9 cm

642,6 cm²

 

 

 

Aire du losange :

 

 d ' : 74 mm

 d :   45 mm

A =74 fois 45) /2 =

A = 3330 mm²/2  =

A =  1665 mm²

 

 

 

 

 

 

 

Interdisciplinarité :

1°) Calculer en cm²  et mm² l'aire d'une feuille  de papier de format A4  .

vérifier qu'elle est égale à  1 / 16ème  m² .

 

210 fois 297 = 62 370   fois 16 = 997920  mm²

 

1 m² = 1 00 00 00 mm² = 1 000 000 mm²

 

1 000 000 : 16  = 62 500  mm²

 

2°)Un cercle a un rayon   de 175 cm . ( prendre  pi = 3,1416 )

Calculer sa longueur , l'exprimer en cm ( résultat arrondi à une décimale ) , puis en m ( arrondir à deux décimale prés).

175  fois 2 fois 3,14 = 1099,56 cm   soit  =  1099,6 cm  ou 10,10 m

 

 

3°) Un disque a un rayon de 52 mm. Calculer son aire , exprimer le résultat en cm² .

 

2 pi R² =  2 fois 3,1416 fois 52 fois 52 = 16989,773 mm²  ou 170 cm²

 

 

4°) un terrain de  hockey sur gazon mesure 91,50 m par 54,90 m . Un terrain de rugby mesure 146,30 m par 68,62m .

Exprimer leurs aires  en m² et hm² .Les classer.

 

Aire du terrain de hockey :  91,50 fois 54,90  = 5023,35 m²  = 0,502335 hm²

Aire du terrain de rugby : 10 039 , 106 m² = 1,0039106 hm²

 

Classement : Aire du terrain de rugby > Aire du terrain de hockey 

 

5°) Une table de ping-pong mesure  274 cm par 152 cm. Quelle est son aire .

274 fois 152 = 38 608 cm²

 

6°)Pour mesurer les dimensions d'un terrain rectangulaire , on reporte un bâton  de longueur 74 cm on trouve :

-         longueur : 47 bâtons + O,60 m.  (  =   ( 74 fois 47  + 60) = 3538 cm)

-         largeur : 31 bâtons .  ( 74 fois 31 = 2294 cm )

Calculer l'aire du rectangle , en m² , arrondie à deux décimales .

  3538  fois 2294 = 8 116 172 cm²    soit   =  811 , 61 m²   à 0,01 prés

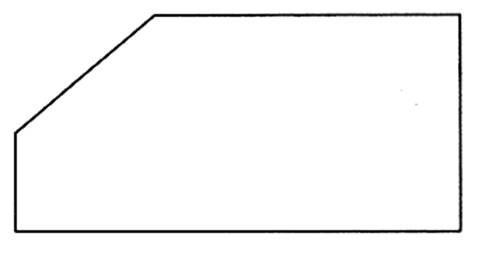
7°)La figure ci - dessous représente une plaque de contreplaquée ( dimension en cm).

Calculer l'aire de cette plaque .

B
 

A
 

 

Conseils : On peut décomposer cette plaque  en trois figures élémentaires ( 3 polygones ) est  un quart de disque . Quelle est la nature de  chaque polygone ? Calculer l'aire de chacun d'eux , celle du quart de disque , puis additionner pour obtenir l'aire de l'ensemble.

Aire du rectangle  A :  40 (  24 - 12)  = 480 cm²

 Aire du rectangle  B :  28 (  40 - 18)  = 336 cm²

Aire du triangle : (12 fois 12) /2  = 72 cm²

Aire du quart de disque :  2 fois 3,14 fois 12 = 75,36 cm²

 

Somme totale : 480 + 336 + 72 + 75,36 =  963 , 36   cm²

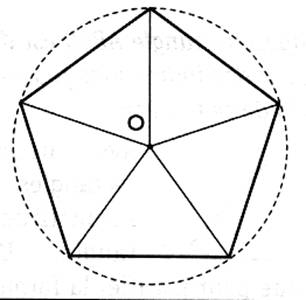
8°) On considère un pentagone  régulier inscrit dans un cercle de rayon 6 cm .

 a)Quelle est la nature  de chacun de ces cinq triangles dont le sommet  est le centre  "O" du cercle .  le triangle est un triangle isocèle  .(  360 ° / 5 =  72° )

b)Donner une mesure de chacun de leurs angles . ( rappel :la somme des angles d'un triangle est de 180 ° )  .  si l’angle au sommet 72° ; la somme des deux autres angles = 180 - 72° = 108 ° ; un angle de base =  108° :2 = 54°

c)Calculer l'aire de ce pentagone . ( pour calculer  "h"  la trigonométrie) .

Aire d’un triangle : il faut savoir calculer la hauteur « h » , distance qui va du centre à la base ? ( voir la trigonométrie )

Hypoténuse = 6 cm ; hauteur : sinus 54°  = 0,809  = h / 6 ; donc   h = 6 fois 0,809 = 4,85 cm ; base : cos 54° = 0,588  = b / 6  = 6 fois 0,588 = 3,53)

Un demi triangle : ( 4,85 fois  3,53  ) / 2 =  17,12 cm² ; il y a 10  demi - triangles équilatéral ; l’aire du pentagone =  17,12 fois 10 = 171,2 cm²

 

9°) Sur  le plan du cadastre à l' échelle  1 / 2 000ème    , une parcelle à la forme d'un trapèze rectangle dont les dimensions sont indiquées sur la figure .

a)calculer l'aire de la figure.  ( 32 + 22) 24 /2 =  648 mm²

b) calculer les dimensions réelles de la parcelle , puis calculer l'aire réelle.(échelle 1 )

1 : 2000 =  0 ,0005 ;   = d : D donc D =  d : 0,0005

 22  devient   22 : 0,0005 =  44000 mm

24   devient  24 : 0,0005 =  48 000 mm:

25   devient 26: 0,0005 =  52 000 mm

32   devient  32 : 0,0005 = 64 000 mm

 

Aire réelle :  (64000 + 44 000) 48 000 / 2 = 2, 592 fois 109  =  2 592 000 000

c) poser le rapport  Aire de la figure sur aire  réelle, exprimer le résultat sous forme d'une fraction de numérateur  égal à 1 .

1 / 4 000 000

 

 

10) Le croquis représente un panneau de particules en bois, dessiné à l'échelle 1 / 4 .

a)     déterminer les dimensions  réelles ( en mm) de ce panneau , en partant des dimensions relevées sur le plan.

b)     Calculer l'aire de ce panneau , exprimer le résultat en dm² et mm² .