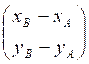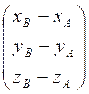Les projections

Index        

Programme    

Objectif suivant

tableau   

TEST

COURS

Devoir  Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle 

Corrigé évaluation 

RESUME     du          COURS

Vecteur

- notion de vecteur

- somme de vecteurs (relation de Chasles)

- produit d’un vecteur par un nombre

-vecteurs colinéaires

-propriétés

Vecteur dans un repère

- les repères du plan

- Composantes et coordonnées cartésiennes d’un vecteur

- distance entre deux points et norme d’un vecteur dans un repère orthonormal

- somme de deux vecteurs (calculs)

- multiplication d’un vecteur par un nombre

- coordonnées du milieu d’un segment

- vecteur de Fresnel

Produit scalaire :

- définition

- propriétés

- expression analytique dans un repère orthonormal

Vecteur dans l’espace :

- Repère de l’espace

- coordonnées d’un point

- coordonnées d’un vecteur

- expression analytique du produit scalaire dans un repère orthonormal

- Norme d’un vecteur dans un repère orthonormal

- distance entre deux points dans un repère orthonormal

- somme de deux vecteurs

- multiplication d’un vecteur par un nombre

- coordonnées du milieu d’un segment

DANS LE PLAN

DANS L’ESPACE

Coordonnées d’un point et d’un vecteur

Coordonnées d’un point et d’un vecteur

Coordonnées d’un point

 Si A ( x_A ; y_A) et B ( x_B ; y_B)

Coordonnées d’un vecteur

Alors  AB

Coordonnées d’un point

Si A ( x_A ; y_A ;z_A) et B ( x_B ; y_B ;z_B)

Coordonnées d’un vecteur

Alors  AB