Pour Aide et Formation Individualisée	CORRIGE TRAVAUX SOMMATIF B. E . P. 10 / 15	Pour aller directement aux informations « cours » voir cas par cas.
INFORMATIONS PEDAGOGIQUES :
DOSSIER N° 9 / 15	Matière : MATHEMATIQUES	►CORRIGE

	TRAVAUX CONTROLE
	Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
	TRAVAUX : EVALUATION
	N°1
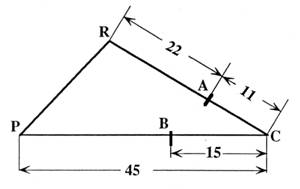
	La figure ci contre étant donnée.(les dimensions sont indiquées sur la figure) Question : Les droites ( AB ) et ( RP) sont -elles parallèles ? Justifier votre réponse.
	Réponse : Oui ! elle doit être justifiée par l’observation de l’égalité de deux rapports convenables. Il faut faire référence explicite à la réciproque du théorème ( énoncé , propriété , …) de Thalès.
	N°2 : On veut passer deux couches de peinture sur toutes les faces d’un cube de 90 cm de côté. Sachant qu’avec un pot on peut couvrir 5 m² au maximum. Combien de pot(s) faudra - t -il acheter ? Expliquer et décrire les calculs. Rédiger la réponse finale.
	Réponse : Calculer l’aire d’une face ; multiplier par 6 puis par 2 . Il faudra 2 pots
	N°3 :
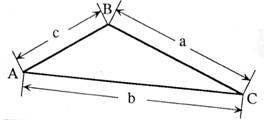
	Dans un triangle rectangle quelconque : b = 10 ; c = 5 et l’angle « A » = 40° Calculer la valeur de « a » à l’unité prés sachant que : a² = b² + c² - 2 b c cos A
	Réponse : 7
??	N°4
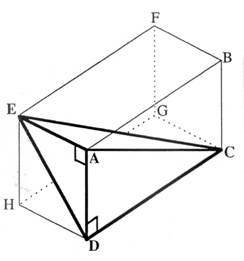
	ABCDEFGH est un parallélépipède rectangle dont les dimensions en cm sont : FB = 3 ; BC = 4 ; HG = 6 Calculer le volume de la pyramide CEAD . Détailler et expliquer . Réponse en cm^3
	Réponse : On peut prendre un des trois triangles comme base.On en déduit alors la hauteur. 12 cm^3
	N°5
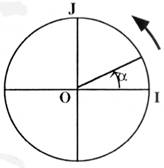
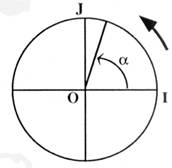
	Le cercle trigonométrique.
	Sur le cercle trigonométrique , placer le point N correspondant à p + a			Sur le cercle trigonométrique , placer le point M correspondant à p - a
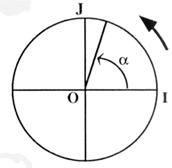
	Compléter, en utilisant les propriétés des fonctions sinus ou cosinus. sin (p + a) = …- sin (a).			Compléter, en utilisant les propriétés des fonctions sinus ou cosinus. cos (p - a) = - cos (a)
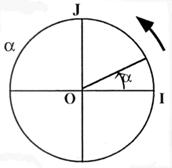
	Sur le cercle trigonométrique , placer le point N correspondant à - a			Sur le cercle trigonométrique , placer le point N correspondant à + a
	Compléter, en utilisant les propriétés des fonctions sinus ou cosinus. sin ( - a) = - sin (a)			Compléter, en utilisant les propriétés des fonctions sinus ou cosinus. Cos ( + a) = sin a
	N°6
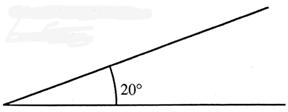
	On a tracé un angle de 20°. Trouver des valeurs approchées de cos 20° et de sin 20° , sans utiliser les touches « sin » et « cos » de la calculatrice. Mais en effectuant des mesures.
	Justifier vos réponses : Mettre en évidence un triangle rectangle et d’un rapport utile au calcul de cos 20° Mettre en évidence un triangle rectangle et d’un rapport utile au calcul de sin 20°
	Résultats obtenus : cos 20° = ; sin 20° = le résultat ne présente pas d’intérêt !!!!!!!!