|
Comme on additionne ou retranche des mètres, des
grammes, des litres..., on additionne ou retranche des tiers, des quarts, des
huitièmes..., à condition qu’il s’agisse
de fractions des mêmes choses.
Comme on dit 3 dL + 4
dL = 7 dL,
On dit 3
dixièmes de L + 4 dixièmes de L = 7 dixièmes de 1L

Règle. Pour additionner des fractions de la même espèce,et qui ont
le même dénominateur, on fait la somme
des numérateurs, et on donne
au résultat le dénominateur commun.
à l’opposé on en déduit que :
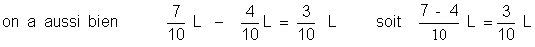
Règle 1. Pour
soustraire des fractions de la même espèce,et qui ont le même
dénominateur, on fait la différence des
numérateurs, et on donne au résultat le dénominateur commun.
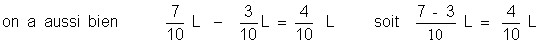
Règle générale : On retiendra que pour additionner ou
soustraire des fractions de la même espèce
( même grandeur) ,et qui ont le
même dénominateur, on fait la somme ou la différence des numérateurs, et on donne au résultat le
dénominateur commun.
Si les fractions n’ont pas le même dénominateur, on
les réduit d’abord au même dénominateur; on additionne ou soustrait ensuite.
1 - effectuer :
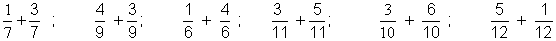
2 . Effectuer :
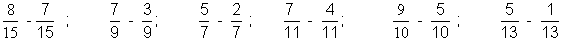
3.
Effectuer : poser les opérations ; seuls deux calculs sont
possibles directement.
attention quatre calculs
ne sont possibles que si l’on a traité la soustraction de
deux nombres relatifs.( cours niveau
V) 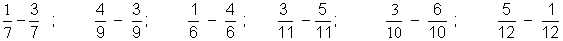
4. Effectuer :
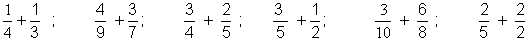
5. Effectuer :
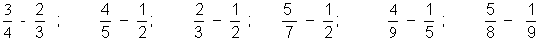
6 . Effectuer : ne faire que les deux
séries d’additions :

7 Effectuez en
choisissant un dénominateur commun aussi petit que possible
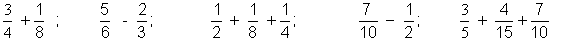
8 . Effectuez,
après avoir simplifié les fractions, puis cherché un dénominateur commun:
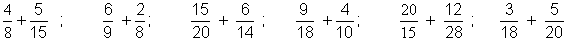
9 . Effectuez,
en remplaçant le nombre entier par une fraction égale
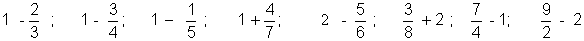
10 . Réduire les fractions suivantes au même
dénominateur, et calculez leur différence.
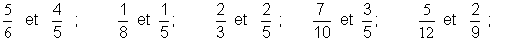
11 . Effectuez,
puis vérifiez en remplaçant les fractions par leur valeur décimale
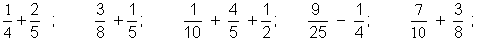
12. Un élève a
eu, en composition, les notes suivantes, sur 10
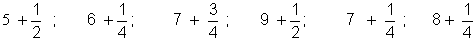 5 5
Calculez le total de ses points, en
additionnant séparément les entiers et
les fractions.
13 . D’un bidon de lait, la crémière a vendu successivement : 2
litres; 1/2L ; 3/4 L ; 1 L
3/4 ; 1 L 1/4 . Il en reste 18 L
3/4 .
a) Quelle quantité de lait a-t-elle
vendue ?
b)
Quelle quantité de lait le bidon contenait-il, avant le début de la vente?
14.
Bruno achète un vélo de 540 €. Il en
paie la moitié comptant, le sixième un mois après. Quelle fraction du prix
a-t-il déjà payée ? Quelle fraction lui reste-t-il à payer ? Combien doit-il
encore ? Vérifiez en calculant chaque versement.
15. Un marchand a vendu les 3/4 d’une pièce d’étoffe; il lui en reste 12 m
à vendre. Quelle fraction de la pièce lui reste-t-il ? Quelle était la
longueur de la pièce d’étoffe ?
16. Trois négociants font venir en commun un wagon de
pommes de terre. Le premier en prend un tiers, le second la moitié, le 3ème le reste. Dites, en sixièmes, la fraction
du wagon prise par chacun. Le wagon
contenait 18 t: combien pèse la part de chacun?
17. Un commerçant a payé le tiers, puis le
quart de ses impôts. Il lui reste à payer 845 € .
a) Quelle fraction du total de ses impôts
représente cette somme?
b) Quel
était le montant de ses impôts ?
c) Quel était le montant de chaque versement ?
Vérifiez.
18. Après avoir roulé pendant 3 h à 25 km par
heure, un cycliste estime qu’il lui reste
les 4 / 9 ( il lui reste 4 tours sur 9 à parcourir ) de son trajet à
parcourir,
a) Quelle
fraction de son trajet a-t-il parcourue?
b) Calculez
la longueur totale du trajet, la distance qu’il a encore à parcourir, et
vérifiez.
19. Un
employé se fait construire une maison;il a un peu d’argent ( 4 800 € ) , et il emprunte ce qui
lui manque, en partie à l’État ( 1/3
de l’emprunt total ) , en partie à
sa famille ( 2/5 de l’emprunt total
) .
a) Quelle fraction du prix de la maison
emprunte-t-il ?
b) De quelle
fraction de ce prix dispose-t-il ?
c) Quel est
le prix de la maison ? Vérifiez.
20. Une fermière a vendu les deux cinquièmes d’un
panier d’oeufs pour 18 €. Il lui reste
15 douzaines d’oeufs.
a) Combien la fermière aurait-elle reçu si elle
avait vendu tous les oeufs ?
b) Combien le panier contenait-il d’oeufs ?
c) Quel
était le prix de vente d’une douzaine d’oeufs ? d’un oeuf ?
20. Dans
un terrain rectangulaire , la largeur du terrain est
égale aux 3/5 de la longueur;
celle-ci mesure 18 m de plus que la
largeur. Quelle est la surface du terrain ?
21. Peut-on prendre successivement la
moitié, le tiers, puis le cinquième d’une barrique de vin ? Si oui ou sinon,
dites pourquoi. S’il reste 38 L dans la barrique après les deux premiers
prélèvements, dites quelle est la contenance de la barrique, et vérifiez.
22. De son compte en banque, un commerçant
a retiré le tiers, puis le quart, puis le sixième. Quelle fraction de son
avoir a-t-il retirée ? (Calculez en douzièmes). il reste, après ces retraits,
12 460 € à la banque. Quel était le
montant du dépôt avant les retraits ? Vérifiez.
|