|
Module : Echelle Application : situation problème. |
DOSSIER : 144 |
|||
|
Warmaths ; Pour Aide et Formation Individualisée ;
REMEDIATION mise à /NIVEAU : niveau VI |
||||
|
TRAVAUX NORMATIFS PRIMAIRE / COLLEGE / LYCEE Matière : MATHEMATIQUES.
Niveau VI |
. |
|||
|
LES
CARTES ROUTIERES |
||||
|
|
||||
|
Info @ cours « carte routière » ; Info @ cours « échelle et matériel » ; |
||||
|
TRAVAUX
CONTROLE |
||||
|
Les questions relatives à « ce qu’il faut
retenir » , au
« savoir » se reporter aux cours . |
||||
|
|
||||
|
|
||||
|
|
||||
|
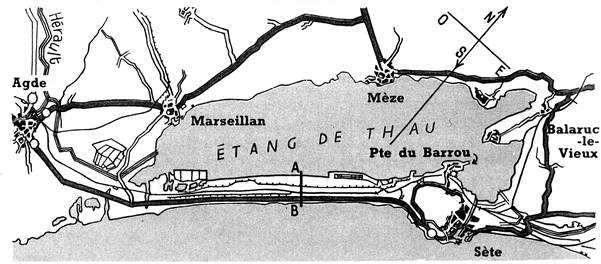
Info : Le fragment ci-dessus de la carte routière est à
l’échelle 1/200 000. Les distances réelles sont 200 000 fois plus
grandes que celles qu’on voit sur la carte;
certaines sont indiquées, le long des routes; pour connaître les autres on
peut 1° multiplier par 200 000 les distances
mesurées sur la carte; 2° utiliser
une échelle graphique : O 1 2 3 4 5km Ici : 1 cm y représente une distance
réelle de 200 000 cm, ou 2 km. |
||||
|
1 .Dessinez une échelle graphique de 15 cm
de longueur, graduée en demi -centimètres : a) Quelle
longueur réelle y représente un demi -centimètre, au 1/200000? b) Quelle longueur
réelle représente toute cette échelle graphique, au 1/200 000? 2. A l’aide de
l’échelle graphique, évaluez la longueur réelle de l’étang dans sa plus
grande dimension. 3. A l’aide d’une règle graduée, mesurez la
distance entre « Marseillan » et la
Pointe du « Barrou » : quel trajet exact
parcourt, en ligne droite (à vol d’oiseau), l’hélicoptère qui va d’un point à l’autre? 4. Sur le littoral de l’étang, marquez un
point à chaque coude important, pour décomposer la ligne sinueuse en une succession
de segments (pas plus d’une dizaine). Mesurez ces segments, totalisez-les et
calculez le périmètre approximatif de l’étang de Thau. 5. Calculez de la même façon les distances
réelles par la route, entre « Balaruc-le-Vieux »
et « Agde » : a) en passant par « Mèze »; b) en passant par « Sète ». Laquelle est la plus courte? Et
de combien? 6. Quelle est la longueur réelle de la route
qui fait le tour de l’étang? 7. Quelle est la longueur qui, sur la carte, représente
2 hm du terrain? Après avoir mesuré, puis calculé, dites à 200 m près la
largeur réelle de l’étang en face de « Mèze ». 8. Quelle est la largeur réelle du cordon
littoral entre les points A et B? Sur quelle largeur de terrain y passent la
route et la voie ferrée qui vont de « Sète » à « Agde »? |
||||
|
PARTIE II |
||||
|
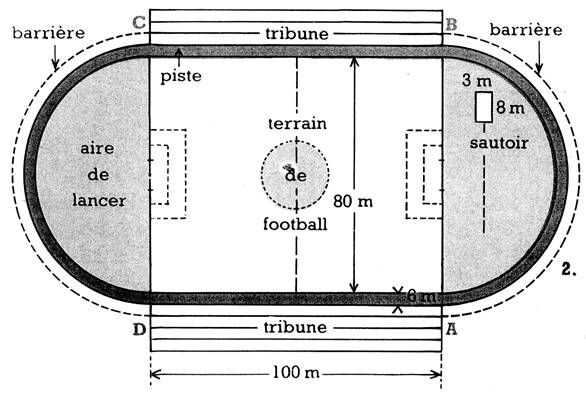
Voici le plan d’un stade, à l’échelle 1 / 2 000. |
||||
|
|
||||
|
1 -
Dites la longueur réelle représentée par 1
cm du plan; par 1 mm. 2. Reproduisez ce plan à l’échelle 1:1000; par combien multipliez-vous les dimensions que le plan a sur ce document ? A ) Longueurs 3. Quelle est
la longueur de la piste, à la corde (à
l’intérieur)? 4. Quelle est
la longueur du bord extérieur de la piste? 5. Les deux
parties droites de la piste sont bordées par des tribunes; mais à 2 m des
bords extérieurs de la partie circulaire de la piste, on a placé une barrière
en ciment armé quelle est sa longueur? 6. Dans une
course de 1 000 m, le
départ a lieu en ligne (coureurs sur une même ligne), la distance étant
mesurée à l’intérieur de la piste. Combien les coureurs ont-ils de tours à
faire? L’arrivée se faisant en A (venant de D), repérez sur le plan la
ligne où se donnera le départ. 7. Dans une course,
le départ est donné entre B et C (à peu près au milieu). Les coureurs
effectuent 6 tours complets, plus la distance entre le départ et la ligne
d’arrivée. Évaluez la distance parcourue. De quelle course s’agit-il
vraisemblablement? Surfaces 8. Quelle est
la surface du terrain de football? Un jardinier en tond le gazon. Il met 2 heures pour tondre un are. Combien de temps lui
faut-il pour tondre tout le terrain? 9. Quelle est
la surface de l’aire de lancer? 10. Sur la partie
rectiligne de la piste entre D et A, abîmée par les courses de vitesse, on
remplace le mâchefer, à raison de 2 brouettées de 45 dm3 par mètre
carré. Quel volume de mâchefer remplace-t-on ? 11. Quelle est
la surface totale de la piste? Volumes 12. On garnit
le sautoir d’une épaisseur de 20 cm de sable neuf à 203 € le m3. Le transport coûtant 4,60
€ par tombereau de 1,2 m3,
quelle est la dépense? 13. Dans la
partie droite entre B et C on va répandre une épaisseur de 5 cm de mâchefer.
Le camion qui apporte ce mâchefer en contient 6 m3.
Combien faut-il de camions? Le camion dépose régulièrement, sur le bord de la
piste, des tas de 1,5 m3.
Quelle est la distance entre 2 tas? 14. On répand sur
l’aire de lancer 20 camions de sable d’une contenance de 5,2 m3.
Quelle est, en cm, l’épaisseur de la couche de sable répandue? |
||||