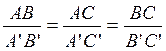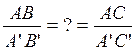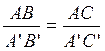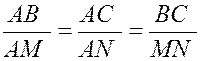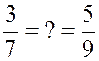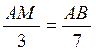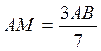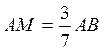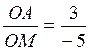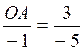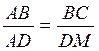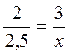Retour vers la leçon Leçon	Titre
N°	CORRECTION : TRAVAUX d ’ AUTO - FORMATION sur THALES

TRAVAUX N° d ’ AUTO - FORMATION : CONTROLE

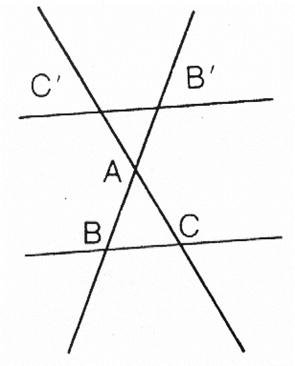
1°) Enoncer le théorème de Thalès.

i9

Propriété de Thalès

:i

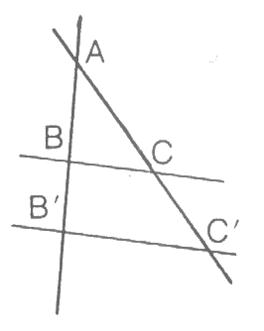
Droites Parallèles à deux droites sécantes: Si la droite (BC) et (B'C') sont parallèles alors:

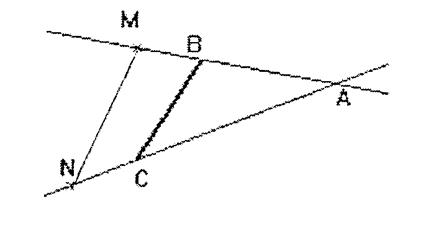
2°) Enoncer la propriété de Thalès.

i9

Réciproque de Thalès.

:i

Deux droites sécantes , on établit une rotation de centre A du triangle C'A B' tel que AC et AC' se superpose. On établit le rapport : Conclusion : si alors (BC) et (B'C') sont parallèles.

3°) Enoncer la réciproque de Thalès.

TRAVAUX N° d ‘ AUTO - FORMATION EVALUATION

Série 1 :

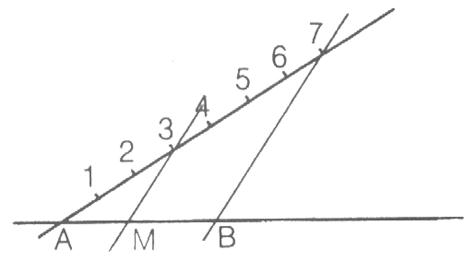
Exercice 1 : ( 3 pts.)

On donne ( en cm) :

AM = 7 ; AB = 3 ; AN = 9 ; AC = 5

Les droites BC et NM sont-elles parallèles ? justifier

D’après la propriété de Thalès : BC et MN sont parallèles si on vérifie que les rapports suivants sont égaux :

Si …………..

Donc : on se pose la question :

On fait le produit en croix : 3 x 9 = 27 ; 7 x 5 = 35 ;

Il s’avère que 3/ 7 et 5/9 ont des résultats différents . On peut en conclure que les droites BC et NM ne sont pas parallèles.

Série 2

1°) calcul d'une mesure (longueur).
On établit : On conclut : ou

2°) Abscisse d'un point dans un repère cartésien non ortho , non -normal.
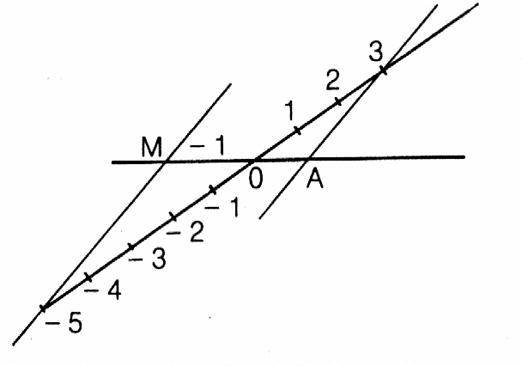
Soit une droite graduée dont OM = -1; on demande de calculer l'abscisse du point "A". On établit : ; soit On en déduit par le produit en croix que A à pour abscisse

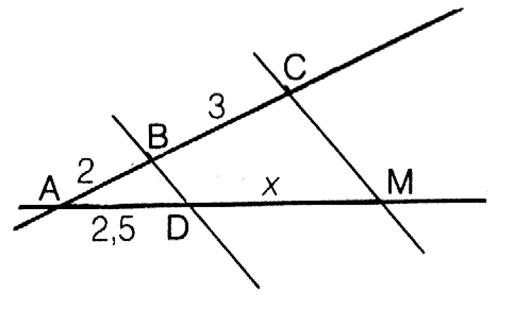
3°) recherche de la longueur d'un quatrième côté
On est dans la "quatrième proportionnelle" On écrit : On remplace : On en déduit (produit en croix et résolution) Que x = 3,75