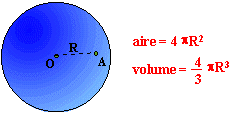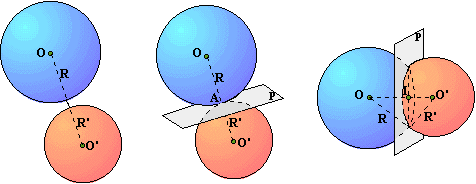WARMATHS

Sphère

Chapitres :
	Définitions.
	Propriétés
	Patron
	Positions relatives d'une droite et d'une sphère
	Positions relatives d'un plan et d'une sphère
	Positions relatives de deux sphères
	Sections planes d'une sphère.
	Formules

Définitions:

Nous définirons la sphère de deux façons:

1. Une sphère est un solide constitué de points de l'espace tous à la même distance d'un point appelé « centre de la sphère ». Cette distance est le « rayon de la sphère ».

Une sphère pleine est une « boule ».

2. Une sphère est un solide de révolution engendré par la rotation d'un demi-cercle de centre O et de diamètre [AB] autour de (AB). Si, au lieu d'un demi-cercle, nous utilisons un demi-disque, le solide ainsi engendré est une boule. Le point O est le centre de la sphère (ou de la boule) et [AB] en est un diamètre.

La droite (AB) est l'axe de révolution. C'est aussi un axe de symétrie pour la sphère.

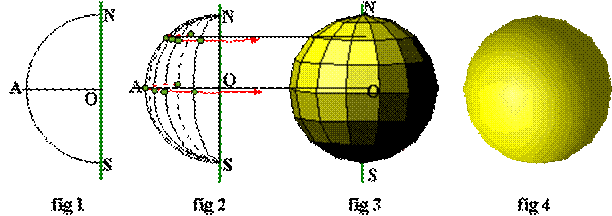
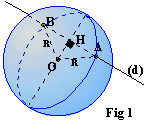
fig 1: Représentation du profil par le demi-cercle de diamètre [NS] et de l'axe de révolution en vert .

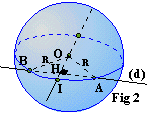
fig 2: Vue légèrement par dessus. Dessinées en pointillés, quelques positions du profil sont représentées. La rotation autour de l'axe (NS) se fait ici, dans le sens contraire des aiguilles d'une montre (indiqué par une petite flèche rouge).

fig 3: La sphère est représenté par 8 positions du profil. Les faces ont été constituées par des petits morceaux de plan (facettes).

fig 4: Toutes les positions du profil ont été représentées. La sphère n'a qu'une face..

Propriétés:

La sphère (et la boule) ne possède qu'une face.

Par construction l'axe de révolution est un axe de symétrie pour la sphère.

Il existe une infinité d'axes de symétrie pour une sphère donnée: ces axes passent tous par le centre de la sphère (ce sont tous les diamètres de la sphère).

Patron:

Un patron est un dessin "à plat" du solide après l'avoir "déroulé. Ce dessin permet, après découpage, de façonner une réplique du solide dans l'espace.

Il n'existe pas de patron pour la sphère.

Nous pouvons matérialiser une sphère à l'aide de matériaux souples et déformables, ou en assemblant des petits morceaux de plan (facettes) comme pour un ballon de football. Ce ne sont que des approximations.

Une boule peut être matérialisée dans du métal ou du bois en utilisant une machine appelée "tour". Dans du métal nous pouvons aussi utiliser les méthodes des "fondeurs" (qui utilisent le métal fondu).

Positions relatives d'une droite et d'une sphère:

Soit une droite (d), une sphère de centre O et de rayon R.

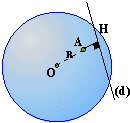
Le point H est un point de (d) tel que (OH) est perpendiculaire à (d). dans ce cas: OH est la distance du point O à la droite (d).

(d) est extérieure à la sphère:

OH>Rayon Malgré les apparences la droite (d) ne coupe pas la sphère. La droite (d) et la sphère n'ont aucun point commun. Le segment [OH] coupe la sphère en A. Comme A est un point de la sphère alors OA=Rayon. (d) est extérieure à la sphère.

(d) est tangente à la sphère:

OH=Rayon La droite (d) et la sphère n'ont qu'un point commun. Le point H est sur la sphère: c'est le point de tangence. Par rapport à la figure précédente: le point A est confondu avec le point H. La droite (d) est tangente à la sphère. Si (d) est tangente à la sphère en A alors il existe un grand cercle tangent à (d) en A. Ce grand cercle est dans le plan contenant la droite (d) et le centre de la sphère (représenté en gris clair sur la figure).

(d) est sécante à la sphère:

OH < Rayon

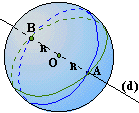
Cas particulier: Si (d) passe par le centre de la sphère alors (d) est un diamètre de la sphère. (D) est sécante à la sphère. Les points d'intersection A et B de (d) et de la sphère, sont diamétralement opposés sur la sphère. Il existe une infinités de grands cercles qui admettent [AB] comme diamètre (nous en avons représenté deux en vert et en bleu sur la figure).

Cas général: Sur la figure 1, (d) pénètre dans la sphère par la partie visible en A et en "ressort" par la partie non visible, celle qui est "derrière". La partie de (d) qui se trouve à l'intérieur de la sphère est le segment [AB] qui se prolonge par un petit segment en pointillé qui est la partie de (d) qui est à l'extérieur de la sphère mais encore cachée par elle. Sur la figure 2, (d) pénètre dans la sphère par la partie visible en A et en ressort par la partie visible en B. La représentation de (d) diffère légèrement (des pointillés seulement sur [AB]) mais cette différence est importante si vous désirez donner une impression de profondeur dans votre figure. Par ailleurs ces "petits" détails montrent que vous appréhendez correctement la position de (d) par rapport à la sphère et vous aident à étudier les propriétés de la figure. Il n'existe qu'un seul grand cercle passant par A et B (représenté en bleu sur la figure). Comme (OH) est un diamètre perpendiculaire à la corde [AB] alors (OH) est médiatrice de [AB].

Positions relatives d'un plan et d'une sphère:

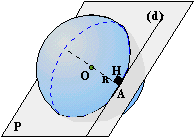
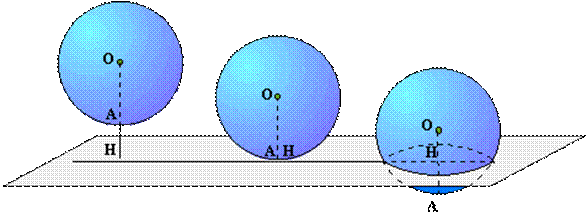
Soit O le centre de la sphère de rayon R. Le point H est tel que la droite (OH) est perpendiculaire au plan. La distance OH est donc la distance du point O au plan. Le point A est le point d'intersection de (OH) et de la sphère. Nous avons donc: OA=R ([OA] est un rayon de la sphère).

OH > Rayon Le plan est extérieur à la sphère.	OH = Rayon Le plan est tangent à la sphère en A. Toutes les droites du plan passant par A sont tangentes à la sphère en A (elles sont perpendiculaires au rayon [OA]).	OH < Rayon Le plan est sécant à la sphère. L'intersection est un cercle dont le centre est sur [OA].

---

Positions relatives de deux sphères:

Nous n'étudierons que les cas où aucune des deux sphères ne contient le centre de l'autre.

Soient deux sphères de centres O et O' et de rayons R et R'. Pour évaluer la position des deux sphères nous allons comparer la distance de leurs centres avec la somme R+R' de leurs rayons.

OO' > R + R' Les sphères n'ont aucun point commun. Elles sont extérieures l'une à l'autre	OO' = R + R' Les deux sphères ont un point commun A qui se trouve dans le plan (P) perpendiculaire à (OO') à la distance R de O (ou R' de O'). Les deux sphères sont tangentes en A.	OO' < R + R' Les deux sphères se coupent suivant un cercle contenu dans un plan (P) perpendiculaire à (OO')en un point I. Les deux sphères sont sécantes.

---

Sections planes:

Une section plane d'une sphère est obtenue en coupant la sphère à l'aide d'un plan.

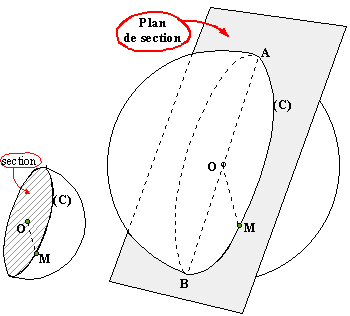
Notes:

Sur les figures de ce chapitre, le plan utilisé est représenté par un parallélogramme colorié en gris afin de donner une impression de relief. Les lignes cachées sont représentées en pointillés. La petite figure montre la section plane correspondante d'une boule.

-passant par le centre de la sphère:

La section d'une sphère par un plan passant par le centre de la sphère est un cercle de même centre et même rayon que la sphère. Ce cercle est appelé grand cercle.

Il existe une infinité de plans passant par le centre de la sphère. Par conséquence il existe une infinité de grands cercles pour une sphère donnée.

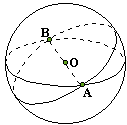
Deux grands cercles d'une sphère se coupent en deux points diamétralement opposés (ces points sont les extrémités d'un diamètre de la sphère (figure ci-contre). Par deux points non diamétralement opposés d'une sphère ne passe qu'un seul grand cercle. Si les deux points sont diamétralement opposés alors nous pouvons faire passer une infinité de grands cercles (comme les pages d'un livre dont la reliure serait le diamètre).

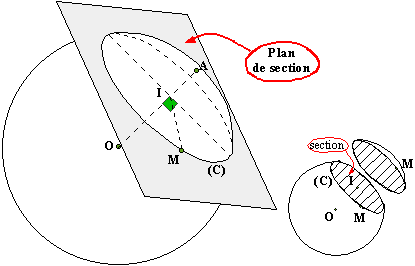
-ne passant pas par le centre de la sphère:

La section d'une sphère par un plan ne passant pas par le centre de la sphère est un cercle dont le rayon est plus petit que celui de la sphère. Ce cercle est appelé petit cercle.

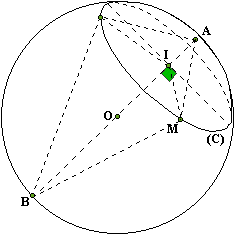
Si I est le centre d'un petit cercle (C) d'une sphère de centre O alors la droite (OI) est perpendiculaire au plan de section. Par conséquence (OI) est perpendiculaire à tous les diamètres de (C) en leur milieu I (I étant le centre du cercle (C) alors I est milieu de n'importe quel diamètre de (C)) ou, autrement dit: (OI) est médiatrice de tous les diamètres de (C).

Soit A et B les points d'intersection de (OI) et de la sphère. Tous les points du petit cercle (C), tel que M, sont équidistants (à même distance) de A. De même tous les points de (C) sont équidistants de B (la distance étant différente). Remarque: [AB] est un diamètre de la sphère et M est un point de cette même sphère. Comme il existe un grand cercle passant par M alors le triangle AMB est un triangle rectangle (pourquoi?).

---

Formules: