WARMATHS	Cercle et Disque.
Définitions et formules. Longueur d'un arc de cercle. Constructions de cercles. Positions relatives de deux cercles. Positions relatives d'un cercle et d'une droite. Définition de la tangente à un cercle. Construction d'une droite tangente à un cercle.

Définitions et formules:

Le cercle de centre O et de rayon R est l'ensemble des points situés à une distance R de O. Ce cercle est noté C(O,R). Un cercle est une ligne courbe fermée, il n'a pas d'aire mais possède une longueur qui se calcule à l'aide de la formule:

P =2. pi.R = 2 p R ( symbole « p » lire « pi »)

où « P » est le périmètre, pi est un nombre valant environ 3,14159... et R est la mesure d'un rayon. Exemple: périmètre du cercle de rayon 5cm=2. pi.5 soit environ 2x3,14 x 5 =31,4cm.

Le disque de centre O et de rayon R est l'ensemble des points situés sur et à l'intérieur du cercle C(O,R). Ce disqpe est noté D(O,R). Un disque est une surface possèdant une aire qui se calcule à l'aide de la formule: A= pi.R² ou pi.R.R

Le disque est la surface colorée.

Appelée « aire »

noté :A_d

( R² est appelé "carré de R" ou "R au carré"). Exemple: aire du disque de rayon 5cm= pi.5² soit environ 3,14x25=78,5cm².

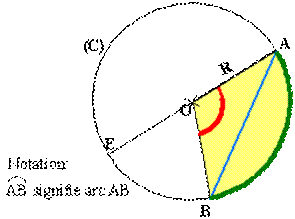
Sur la figure ci-contre: [OA] est un rayon, [AE] est un diamètre (O en est le milieu). Les diamètres sont les axes de symétrie du cercle (et du disque). la corde [AB] est en bleu. l'arc AB est en vert. En fait, deux points A et B sur un cercle déterminent deux arcs (deux "morceaux" de cercle), l'autre, ici, n'est pas mis en couleur. La mesure de l'angle saillant au centre AOB est en rouge (il existe aussi deux angles au centre de même nom). Le secteur angulaire de côtés [OA] et [OB] est représenté en jaune (il existe aussi deux secteurs angulaires de même nom: l'un est rentrant, l'autre est saillant comme celui colorié en jaune). Il s'agit d'une surface qui possède une aire

Longueur d'un arc de cercle:

Pour calculer la longueur d'un arc de cercle il est nécessaire de connaître son rayon de courbure( égal au rayon du cercle qui lui sert de support) et la mesure de l'angle au centre qui lui correspond.

Il y a proportionnalité entre cette mesure( m en degrés par exemple) et la longueur de l'arc ( l en centimètres par exemple) comme il y a proportionnalité entre la plus grande mesure d'angle au centre (360°) et la plus grande longueur d'arc correspondant sur le cercle (cet arc est tout le cercle de longueur 2. pi.R ).

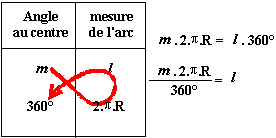
En utilisant les "produits en croix" nous obtenons la formule ci-dessus (inutile de la retenir; il vaut mieux bien comprendre la justification de ce calcul de proportions). Exemple: avec m=60° et R=5cm, nous avons:

l= (60.2 .pi.5):360 soit environ 5,24cm

Constructions de cercles:

Cercles passant par 1 point: Il en existe une infinité, de rayons égaux ou différents

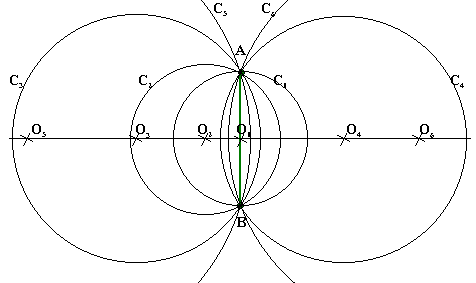
Cercles passant par 2 points: soit le cercle de centre O passant par les points A et B. Nous devons avoir OA=OB. Comme OA=OB alors O se trouve sur la médiatrice de [AB]. Comme la médiatrice de [AB] contient une infinité de points alors il y a une infinité de cercles passant par deux points donnés. Leur centre est sur la médiatrice de [AB]. Essayez de refaire la figure ci-dessous( donnez vous deux points A et B, tracez la médiatrice de [AB] et, pointe sèche sur différents points de cette médiatrice, tracez plusieurs cercles passant par A et B). Sur la figure ci-dessous O₁ correspond au centre du cercle C₁, O₂ correspond au centre du cercle C₂,...

Cercle passant par 3 points: il s'agit du cercle circonscrit à un triangle.

Cercle passant par 4 points: il s'agit du cercle circonscrit à un quadrilatère. Il n'existe que dans des cas particuliers. Les plus connus sont les cercles circonscrits au carré, au rectangle et au trapèze isocèle.

Positions relatives de deux cercles:

Cercles tangents:

Deux cercles sont tangents lorsqu'ils n'ont qu'un point commun (point de contact ou point de tangence).

Ils peuvent être tangents extérieurement (fig 1) ou tangents intérieurement à l'un (fig 2).

Dans les deux cas, les centres et le point de contact sont alignés.

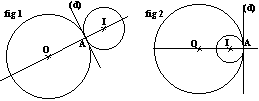
Remarque: (d) est une droite tangente commune (voir paragraphe suivant). C'est la seule tangente commune dans le cas de la figure 2.

Cercles sécants:

Deux cercles sont sécants lorsqu'ils ont deux points communs (points d'intersection).

Ils peuvent être sécants extérieurement (fig 1) ou sécants intérieurement à l'un (fig 2).

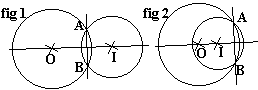
La droite (OI) est appelée droite des centres. La droite (AB) est appelée sécante commune aux deux cercles alors que le segment [AB] est appelé corde commune. La droite des centres est médiatrice de la corde commune (ce qui reste à démontrer!..utilisez le fait que OA=OB et que IA=IB ...).

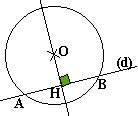
Positions relatives d'un cercle et d'une droite:

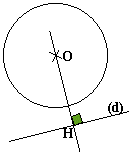
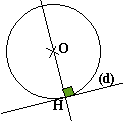
Données: Un cercle de centre O et de rayon R, une droite (d). La distance de O à la droite (d) est OH.

Droite extérieure au cercle	Droite tangente au cercle	Droite sécante au cercle
OH>R Aucun point commun	OH=R Un point commun: le point de contact ou de tangence	OH<R Deux points communs

Définition de la tangente à un cercle:

Une droite (d) est tangente à un cercle de centre O en un point M de ce cercle lorsque (d) est perpendiculaire au rayon [OM] au point M.

Construction d'une droite tangente à un cercle et passant par un point donné:

Point sur le cercle:

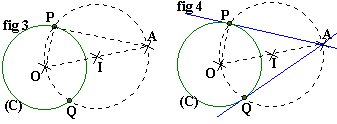
Données: Le cercle (C) de centre O et le point A sur le cercle (C) (fig 1).

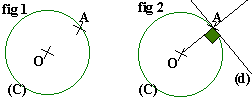
La tangente à un cercle est une droite :

-passant par un point de ce cercle. Ici nous choisirons A bien sûr.

-et perpendiculaire à un rayon du cercle en ce point.

Il suffit donc de tracer la droite (d) perpendiculaire au rayon [OA] et passant par le point A.

Point extérieur au cercle:

Données: Le cercle (C) de centre O et le point A, extérieur au cercle (fig 1).

Tracez le segment [OA] et construire son milieu I (fig 2)

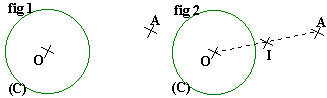
Tracez le cercle de diamètre [OA] (ou: de centre I et de rayon IO ). Ce cercle coupe le cercle donné en deux points P et Q (fig 3).

Comme le triangle OPA (respectivement OQA) est obtenu en joignant le point P (respectivement Q) du cercle de diamètre [OA] aux extrémités O et A de ce diamètre alors OPA (respectivement OQA) est rectangle en P (respectivement en Q).

Tracez les droites (AP) et (AQ). Comme OPA et OQA sont rectangles respectivement en P et Q alors ces deux droites sont perpendiculaires aux rayons [OP] et [OQ] du cercle (C) en des points de ce cercle (fig 4).

Les droites (AP) et (AQ) sont donc tangentes au cercle (C) (et elles passent par A, ce qui était demandé).