dev sommayif corrigé GP et fonct linéaire

ENVIRONNEMENT du dossier :

Index        

Objectif précédent  

Sciences       

Tableau       173a

 

DOSSIER :   LES  PROPORTIONS ;  Corrigé des exercices et problèmes

 

1°) Les deux suites  [ 9 ;11 ;19 ;25 ;31 ;]  et  [27 ; 33 ;57 ;75 ;93 ;] sont - elles des suites de nombres proportionnelles ?

 

9

11

19

25

31

 

27

33

57

75

93

 

 

1) somme des numérateurs :   9+11+19+25+31= 95

2 )somme des dénominateurs =  27+33+57+75+93= 285

3 )division des deux sommes        285:95 =3

4 )division d'un rapport :            27:9 = 3

 

5 )on compare les deux  résultats : 3 et 3 ; les quotients sont égaux

6 ) Conclusion : la suite de rapports est une suite de rapports égaux

 

 

2°) Si l’on paye   dans un restaurant  2400 €   pour  un mois (30  jours)de pension ,que paiera-t-on pour :

5jours ; 12jours ; 21 jours

 

2400 €

X1

X2

X3

 

30

5

12

21

 

 

2400 :30 = X1 :5  ; X1 = 2400 fois 5  : 30 = 400€

X2=        960 €                                  X3 = 1680 €

 

 

 

 

 

3°) Calculer la mesure de la d.d.p. aux bornes d’un résistor dans les cas suivants :

calibre

Echelle

lecture

corrigé

3 V

[ 0 ; 30 [

22 divisions

 =  ;

 

 

    x =22,1 V

 

 

 

4°) Quelle est l’intensité du courant traversant le circuit ?

Calibre

Echelle

lecture

0,1 A

 ( 0 ; 100)

57 divisions == =  ;

 

    x = 0,057  A ou 57mA

 

 

 

 

 

5°)  Une voiture consomme 18,4 l d’essence pour effectuer le trajet Paris - Caen  ( 230 km) .Quelle sera sa consommation pour effectuer le trajet  Paris  - Cherbourg  long de 340 km ?

Que devons nous admettre pour résoudre le problème ?

 

 On pose:        =  ;

 

x = 27,2 l

Conclusion:

Nous considérons que la consommation est constante

La consommation pour 340 km parcourus sera de 27,2 litres

 

 

 

6°) La masse et le volume d’un corps sont deux grandeurs directement proportionnelles .Le coefficient de proportionnalité s’appelle la « masse volumique » du corps.

 

a)    Calculer le volume d’un corps de masse  52 kg dont la masse volumique est  de 23 kg /dm3

On pose :

 =  ;     =  ;

 

Calcul: 52 fois 1 :23

Volume = 2,2608696 dm3

 

 

 

 

7° )  De l’égalité 3,4 x 7,8  =  2,4 x 11,05 ; déduire toutes les proportions possibles.

 

On sait que  est égale à       si     

           

               Extréme.1  "fois"   Extréme.2  =  Moyen .2  "fois"  Moyen.1 ;

 

a)  On remplace  :  3,4  "fois"  7,8  =  2,4  "fois"  11,05

b) on remplace  dans :

                                est égale à  

On sait que : Dans une proportion, on peut permuter les « extrêmes »«  ( l’égalité reste vraie)

traduction mathématique

 

si   =   alors    =    

 

 

 si  =  alors si  =

 

Dans une proportion, on peut permuter les « moyens » ,(l’égalité reste vraie)

traduction mathématique

si   =   alors    = 

donc  :     si  =   alors si  =  ou  =

 

 

Solutions

=

 

=

=

=

 

 

 

 

 

 

 

 

8° ) Calculer x dans chacun des  cas suivants :

 

 

 

 

 = 

x = 2,3 fois 15 : 7,5 =

4,6

 =   

x= 87,12:9,9

8,8

 = 

x= 1,76:6

0,88/3 = 88/300

 

 

 

 

 

9° )  Les deux suites  [ 9 ;11 ;19 ;25 ;31 ;]  et  [27 ; 33 ;57 ;75 ;93 ;] sont - elles des suites de nombres proportionnelles ?

 

S1

9

11

19

25

31

S2

27

33

57

75

93

Calcul S2 sur S1

3

3

3

3

3

Conclusion : les deux suites sont proportionnelles

 

10°)   A et B étant des grandeurs directement proportionnelles , compléter le tableau :

 

Mesure de A

.7

21:3,5

35

63

70

280

700

Mesure de B

2 fois 3,5

6

10

18fois3,5

20

80

200fois 3,5

Recherche de k

 

 

B fois 3,5 = A

 

 

 

 

 

 

 

 

 

 

11°) Idem.

 

 

10

11

15

24

27

2

2,2

3

4,8

5,4

 

 

3 fois 5=15

 

 

 

12°) La suite de nombres S1  [3,5 ;5,7 ;4 ;9] est proportionnelle à la suite de nombres S2 [a ;b ;c ;d] Le coefficient de proportionnalité S1 sur S2  est de  3 . Calculer a ;b ;c ;d

 

 

3,5

5,7

4

9

K=3

10,5

17,1

12

27

 

 

 

 

 

 

14 ) La longueur (L) du cercle est donnée en fonction du  diamètre (D); compléter le tableau suivant :

 

D

5

10

12

25

28,2

L

15,7

31,4

37,68

78,5

88,548

 

Les deux grandeurs sont-elles proportionnelles ?

Les grandeurs sont proportionnelles  :puisque "pi" est égal à "k" 

 

15 °) Un cycliste parcourt 12km en 45mn .Un autre 17km en 50mn .Les distances parcourues sont-elles  directement proportionnelles aux durées du parcours ?

 

12: 45 =0,26666666

17:50 =0,34

Conclusion: Les distances parcourues ne sont pas  directement proportionnelles aux durées du parcours

16° )Trois associés ont investi dans la même entreprise :le premier :10 000 €    ,le deuxième :       14 000 €   ;le troisième :26 000€   . Ils ont gagné 13 680  €  .

     Partager le gain proportionnellement aux mises des associés .

 

Somme investie :

 

14000+10000+26000=50000

 

Le premier aura :

fois 10000

 

2736

Le deuxième aura

fois14000

 

3830,40

Le troisième aura

fois 26000

 

7113,60

 

                  Total =

13680

 

 

 

17°  ) De l’égalité 3,4 x 7,8  =  2,4 x 11,05 ; déduire toutes les proportions

 

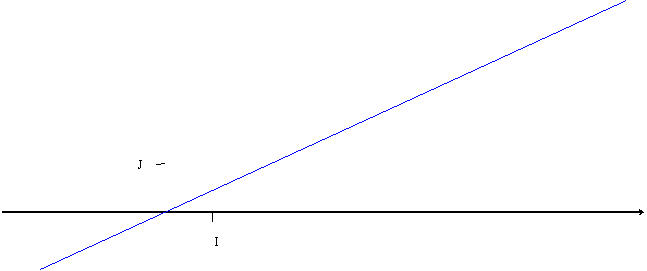
18 °  )  Dans le  repère ci dessous  , la droite D2 représente la fonction g2.

Question : Compléter le tableau suivant :

 

x

-3

 

1,5

 

6,5

 

g2

 

-1

 

3

 

 

 

 

19° )  Représenter graphiquement les fonctions f3(x) et f4(x) dans ce même repère  (O,I,J)

 

f3(x) = -1,5 x

f4(x) =   3x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  Compléter le repère :

 

 

 

 


O

D2