TRAVAUX : IUFM
série 1
|
|
Un
cultivateur a vendu les 5/9 de sa récolte , puis les 2/5 de ce qui lui reste
à la coopérative. Quelle fraction de la quantité initiale lui reste - t -il
pour élever ses volailles . |
4/15 |
|
|
Soit
ABC un triangle rectangle en A tel que AC = |
422
cm² |
|
|
Parmi
les fractions 4/5 ; 1/3 ; 3/ 36 ; 71 /
50 ; 5 / 70 ; 9 /36 ; quelles sont celles qui peuvent être
converties en nombre décimal. On justifiera par une méthode autre que celle
qui consiste à effectuer la division. |
4/5 71/50 9/36 |
|
|
Une
chèvre est attachée dans une pâture au bout d’une corde de |
120+2511198,57 m² |
|
|
Après
avoir augmenté son avoir des 2 / 15, un spéculateur perd ensuite les 3/8 de
son nouvel avoir. Il lui reste alors 58 437 ,50 €. Trouver son avoir
initial. |
82 500
€ |
|
|
Un
commerçant propose à ses clients deux sortes de baril de la même lessive. Ces
barils ont la même forme cylindrique, mais les dimensions de l’un sont égales
aux 9/10 ce celles de l’autre. ; Le prix du petit est les 7/10 de celui
du grand. Quel est le bail le plus économique pour le client ?
Justifiez la réponse. |
Le
plus petit car Pp / Vp = 0,7 Pg / 0,729 Vg = 0,96 ( Pg/Vg) |
|
|
Un
ballon de Quelle
est la ficelle qui sera la plus rallongée ? On
rappel que le rayon de la terre est d’environ 6400 km . |
Elles
seront rallongée de |
|
|
On
donne un cercle de centre A. 1°°
Tracer un losange ABCD tels que les 3 autres sommets B, C , D soient situés
sur le cercle. Tracer un carré inscrit dans le cercle de centre A. 2°)
Calculer la mesure du rayon de ce cercle, sachant que l’aire du carré est de
200 cm². Puis calculer l’aire du losange., |
5023
cm² |
|
|
Un
mobile parcourt la distance AB à la vitesse moyenne de AB = 1 km ; BC = 1 km ; AC = |
|
|
|
1°
Analyser la figure ci contre et
établir un programme de construction, à la règle non graduée et au compas,
permettant de la reproduire sans la voir. 2°)
On pose AB = 3a où « a » est une longueur donnée . On se propose
de calculer l’aire de l’ovale en
fonction de « a ». a)
Quelle est la nature
du triangle OCD ? en déduire la mesure de l’angle MON. b) B)calculer en fonction
de « a » l’aire du demi-
ovale AMNB. c)
C)En déduire l’aire de l’ovale entier , en fonction de « a ».i? |
OCD
est équilatéral ; a²(41-23)/4 ; a² (41- 23) /2 |
|
|
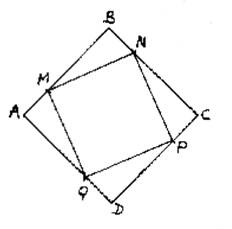
Soit
la figure ci contre où ABCD est un carré de côté « a » et
« M », N ;, P , Q quatre points tels que AM = BN = CP = DQ = x
avec 0<x < a . Les
triangles AMQ , BNM , BPN , DPQ sont donc égaux . 1°
Montrer que l’angle QMN est droit. 2°
En déduire que le quatrième MNPQ est un carré. 3°
Calculer la longueur « c » commune de [MN] , [NP] , [PQ ]
, [QM]
en fonction de « a » et de « x ». 4°
Calculer l’aire du carré MNPQ |
1° on calcule, 3° 22x² -
2ax + a² ; 4° 2x² - 2ax +a² |
TRAVAUX : IUFM
, série 2
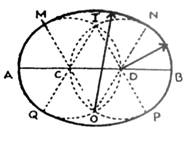 Ovale
au tiers -point d’axe AB
Ovale
au tiers -point d’axe AB