Probabilités

Probabilités

1- Trois personnes entrent dans une pièce où se trouvent 7 chaises différentes. De combien de manières différentes peut-on placer les 3 personnes?

Réponse : $A_7^3 = \frac{7!}{4!} = 210 $

$\diamond$

2- Quel est le nombre maximum d'immatriculations qu'il est possible de réaliser dans le cas des immatriculations de véhicules français?

3- Un train de marchandises se compose de 14 wagons dont 6, 3, 4 et 1 sont à laisser respectivement en 4 gares différentes, A, B, C, D. De combien de manières ces wagons peuvent-ils être disposés pour que les wagons à retirer soient toujours en queue de train?

4- Soient $A$, $B$et $C$des évènements aléatoires définis sur une même épreuve. On considère maintenant deux nouveaux évènements : $E_1 = A \bigcap B^c \bigcap C^c$et $E_2 = A \bigcap (B \bigcup C)$. (a) Montrer que $E_1$et $E_2$sont incompatibles. (b) Que signifie l'évènement $E_1 \bigcup E_2$? (c) Calculer $P(E_1)$et $P(E_2)$sachant que $P(A) = 0.6$, $P(B) = 0.4$, $P(C) = 0.3$, $P(A \bigcap B) = 0.2$, $P(B \bigcap C) = 0.1$, $P(A \bigcap C) = 0.1$et $P(A \bigcap B \bigcap C) = 0.05$.

5- Un circuit électronique est composé de $10$blocs identiques en série, chacun de ces blocs peut être formé d'un élément unique ou de deux éléments identiques en parallèle (dans ce cas on supposera qu'il suffit qu'un des deux éléments fonctionne pour que le bloc fonctionne). On admet que chaque élément a une probabilité égale à 0.02 de tomber en panne pendant les 5000 premières heures de fonctionnement et que les pannes des divers éléments sont des évènements indépendants. Calculer les probabilités d'une panne de circuit pendant les 5000 premières heures de fonctionnement, si chaque bloc est formé d'un seul élément(a), si chaque bloc est formé de deux éléments(b), si $n$blocs sont fomés d'un seul élément(c). Combien faut-il de blocs à $2$éléments pour garantir une probabilité de panne du circuit inférieure à $10\%$(d).

Réponse : (a) 0.18 (b) 0.004 (c) $1 - (1-0.02^2)^{10-n} (1-0.02)^n$(d) 5

$\diamond$

6- On dispose de $N$boules dont $D$sont rouges. On tire (sans remise) $n$boules. Quelle est la probabilité de tirer $d$boules rouges ?

Réponse : 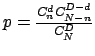$p = \frac{C_n^d C_{N-n}^{D-d}}{C_N^D}$

$\diamond$

7- La demande d'un produit $P$pendant $1$mois peut prendre les valeurs $d$suivantes avec les probabilités $P(d)$:

\begin{displaymath}(d,P(d)) \in \{(0,0.1), (1,0.1), (2,0.2), (3,0.3), (4,0.2), (5,0.1) \} \end{displaymath}


a) Pourquoi peut-on parler de probabilité ?

b) De quel stock minimum doit-on disposer en début de mois pour que le risque de rupture de stock soit inférieur ou égal à $0.3$?

8- On sait que les jumeaux peuvent être de vrais jumeaux, dans ce cas ils ont même sexe, ou de faux jumeaux, et dans ce cas la probabilité pour qu'ils aient même sexe est $0.5$. On suppose connue la probabilité $p$pour que deux jumeaux soient de vrais jumeaux. (a) Déterminer en fonction de $p$la probabilité pour que deux jumeaux soient de même sexe. (b) Déterminer la probabilité pour que deux jumeaux soient de vrais jumeaux sachant qu'ils ont même sexe.

Réponse : (a) $\frac{1+p}{1}$; (b) $\frac{2p}{1+p}$

$\diamond$

9- Les clients d'une entreprise ont été répartis en plusieurs catégories en fonction du volume d'affaires annuel traité avec eux et en fonction du fait que l'on a déjà eu pour eux ou non des créances impayées. Les résultats de ce décompte sont donnés dans le tableau ci-dessous:

Volume d'affaire annuel

0 à 10 000 ($C_1$)

10 000 à 100 000 ($C_2$)

+ de 100 000 ($C_3$)

Clients ayant déjà eu des impayés ($I$)

100

25

10

Clients n'ayant jamais eu d'impayés (${\overline I}$)

1 200

350

150

Déterminez pour un client choisi au hasard les probabilités suivantes: $P(C_1)$, $P(C_2)$, $P(C_3)$, $P(I\vert C_1)$, $P(I\vert C_2)$, $P(I\vert C_3)$, $P(C_1\vert I)$, $P(C_2\vert I)$, $P(C_3\vert I)$. Y a-t-il dépendance entre le volume d'affaires et l'existence d'impayés ?

Réponse : $P(C_1)=0.708$, $P(C_2)=0.204$, $P(C_3)=0.088$, $P(I\vert C_1)=0.08$, $P(I\vert C_2)=0.07$, $P(I\vert C_3)=0.06$, $P(C_1\vert I)=0.74$, $P(C_2\vert I)=0.19$, $P(C_3\vert I)=0.07$. Il y a dépendance entre le volume d'affaires et l'existence d'impayés d'après l'analyse des termes $P(C_i~et~I)$et $P(C_i)P(I)$.

$\diamond$

10- Pour juger de l'efficacité d'une campagne publicitaire ayant porté sur un produit $P$, on a sondé $1 500$personnes, $1 000$dans une région $R_1$et $500$dans une région $R_2$. Seule la région $R_2$avait été concernée par la campagne. Les résultats sont les suivants:

 

Connaissent le produit $P$et le consomment

Connaissent le produit $P$et ne le consomment pas

Ne connaissent pas le produit $P$

Région $R_1$

80

150

770

Région $R_2$

50

130

320

a) Déterminer pour chacune des régions: la probabilité qu'une personne connaisse le produit $P$, la probabilité qu'une personne consomme le produit $P$et la probabilité qu'elle consomme le produit $P$sachant qu'elle le connait.

11- La probabilité pour qu'une ampoule électrique ait une durée de vie supérieure à $2$ans est de $0.2$. Sachant qu'un lustre est formé de 5 ampoules, donnez la loi modélisant le phénomène "il faut changer n ampoules en $2$ans" et les probabilités correspondant aux valeurs $0$et $5$de $n$.

Réponse : L'évènement "une ampoule à changer" peut être modélisé par une loi $(0,1)_{p=0.8}$. La loi de l'évènement "il faut changer une ampoule en $2$ans" est donc une loi binomiale (si l'on suppose l'indépendance entre les $5$ampoules). $P(0)=C_5^0 0.8^0 0.2^5 = 0.00032$et $P(5) = 0.32768$.

$\diamond$

12- Soient deux urnes contenant respectivement 100 boules rouges et 100 boules noires. On prend 32 boules rouges de la première urne pour les mettre dans la seconde, puis on mélange et on reprend 32 boules de la 2ème urne pour les remettre dans la première. Quelle est la probabilité qu'il y ait plus de boules rouges dans la première urne que dans la deuxième ?

13- Un lot de $n$articles présente un mélange des produits de trois usines : $n_1$articles de l'usine $U_1$, $n_2$de l'usine $U_2$et $n_3$de l'usine $U_3$. Pour les articles de l'usine $U_1$, la probabilité de fonctionner sans défaillance pendant un temps $\tau$est $p_1$, $p_2$pour l'usine $U_2$et $p_3$pour l'usine $U_3$. On tire au hasard un article, calculer la probabilité que l'article fonctionnera sans défaillance pendant un temps $\tau$.

14- On considère trois lots d'articles de même type, le premier compte $d_1$articles défectueux parmi les $n_1$articles. De même, on compte $d_2$(resp. $d_3$) articles défectueux parmi les $n_2$(resp. $n_3$) articles du deuxième (resp. troisième) lot d'articles. On choisit au hasard l'un des lots pour en tirer au hasard deux articles. Le premier article est défecteux. Quelle est la probabilité que le second article soit défecteux lui aussi ?

Réponse : Soient les états $D_1$et $D_2$indiquants que les premier et deuxième articles sont défecteux. Ce que l'on cherche est donc $P(D_2\vert D_1)$.

En se servant de la formule de Bayes, on a

\begin{displaymath} P(D_2\vert D_1) = \frac{P(D_1 \bigcap D_2)}{P(D_1)} \end{displaymath}


Les deux articles provenant d'un des trois lots, on introduit les lots par

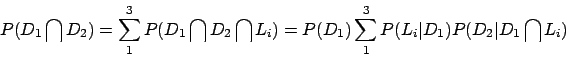
\begin{displaymath} P(D_1 \bigcap D_2) = \sum_1^3 P(D_1 \bigcap D_2 \bigcap L_i) = P(D_1) \sum_1^3 P(L_i\vert D_1) P(D_2\vert D_1 \bigcap L_i) \end{displaymath}


donc

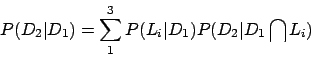
\begin{displaymath} P(D_2\vert D_1) = \sum_1^3 P(L_i\vert D_1) P(D_2\vert D_1 \bigcap L_i) \end{displaymath}


De la même manière, on estime les autres probabilités conditionnelles par

\begin{displaymath} P(L_i\vert D_1) = \frac{P(D_1 \bigcap L_i)}{P(D_1)} = \frac{P(L_i) P(D_1\vert L_i)}{\sum_1^3 P(L_i) P(D_1\vert L_i)} \end{displaymath}


Les probabilités qui nous sont nécessaires sont

 

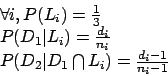
\begin{displaymath} \begin{array}{l} \forall i, P(L_i) = \frac{1}{3}\\ P(D_1\ve... ...D_2\vert D_1 \bigcap L_i) = \frac{d_i - 1}{n_i - 1} \end{array}\end{displaymath}


donc

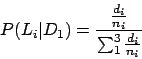
\begin{displaymath} P(L_i\vert D_1) = \frac{\frac{d_i}{n_i}}{\sum_1^3 \frac{d_i}{n_i}} \end{displaymath}


Le tout recombiné donne

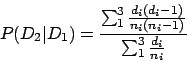
\begin{displaymath} P(D_2\vert D_1) = \frac{\sum_1^3 \frac{d_i(d_i-1)}{n_i(n_i-1)}}{\sum_1^3 \frac{d_i}{n_i}} \end{displaymath}


$\diamond$

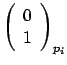15- Soient deux v.a. discrètes indépendantes $X_i$de type $\left(\begin{array}{l}0\\ 1\end{array} \right)_{p_i}$( $P(X_i = 1) = p_i$). (a) Déterminez la loi de la v.a. $Z_1 = min(X_1,X_2)$. (b) Déterminez la loi de la v.a. $Z_2 = max(X_1,X_2)$. (c) Déterminez la loi du couple $(Z_1,Z_2)$. (d) Les v.a. $Z_1$et $Z_2$sont elles indépendantes ?