Le second degré : Pb D'APPLICATION

1°) Déterminer la valeur de la résistance x pour que les montages ci-dessous soient équivalents :

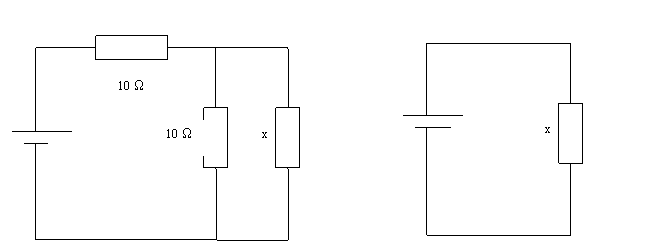
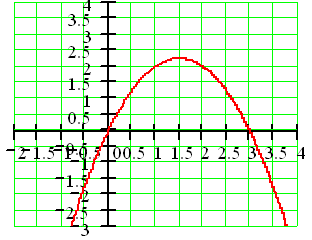
2°) La courbe C est la courbe représentative de la fonction f définie sur l'ensemble des réels par

f(x) = -x² + 3x

a) Résoudre graphiquement l'équation -x² + 3x = 0

b) En utilisant le graphique indiquer le nombre de solutions des équations f(x) = 1 f(x) = 2,25 f(x) = 4

c) En utilisant les formules de résolution, résoudre les équations :

-x² + 3x = 4 -x² + 3x = 2,25 -x² + 3x = 1

NB : on donnera les valeurs exactes des solutions puis les valeurs arrondies au centième.

3°) La distance de freinage d’un véhicule est imposée par une circulaire officielle.

Elle est donnée par la formule suivante :

où

d est la distance de freinage en mètres,

v la vitesse du véhicule en début de freinage en km/h,

f le coefficient de frottement des pneus sur la route dans les conditions normales ( route sèche). f=0,4,

a est la pente de la route ; dans le cas d’une montée a>0 ( si la pente est de 10% alors a = 0,1) dans le cas d’une route horizontale a=0, dans le cas d’une descente a<0 (si la pente est de 5% alors a=-0,05)

Le coefficient 0,55 est le temps de réaction de l’automobiliste.

a. Calculer la distance de freinage pour v =130 km / h dans les cas suivants :

i. Sur une route horizontale

ii. Sur une montée de 6%

iii. Sur une descente de 6%

b. Calculer la vitesse à ne pas dépasser pour s’arrêter sur 100 m dans une descente de 8%

3°) Deux villages A et B sont distants de 60 km. Vous allez de A à B à la vitesse v ( en km/h) et vous revenez de Bà A à la vitesse v+15. Le temps de parcours est de 6 h. Quelle votre vitesse v ?