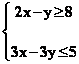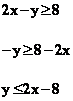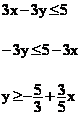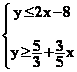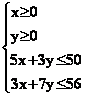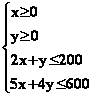PREMIER
DEGRE
En mathématiques, une égalité
est une relation contenant un signe égal : « = ».
Il signifie que les grandeurs
situées à gauche (premier membre) ainsi quà droite (second membre) sont
équivalentes (ou égales)
REGLES GENERALES DE
TRANSFORMATIONS DUNE EGALITE
Pour
transformer une égalité en mathématiques on a le droit dadditionner, de
soustraire, de diviser ( nombre non nul ), ou de
multiplier par un même nombre les deux membres de légalité.
Exemple : 2
= 2
Jajoute 3 aux deux
membres : 2+3=2+3
Légalité devient : 5 = 5 ect ............
équation du premier degré à
une inconnue
Définition :Une équation
possédant une inconnue ( "x" généralement ) est une égalité qui n'est
pas vraie pour n'importe quelle valeur donnée à cette inconnue .
Le signe " = " sépare les deux "membres"d'une
équation. Elle est du premier degré lorsque la puissance de linconnue est 1 au
maximum.
Exemple : 3x + 2 = 7
Rappel : lorsquil ny a pas de signe dopération entre
une lettre et un nombre, cest le signe multiplié qui est sous entendu :
3x+2 : signifie je
prends un nombre « x » je le multiplie par 3 et jajoute 2 au
résultat.
Par définition, la solution
dune équation est le nombre qui substitué à la lettre permet à légalité
dêtre vérifiée.
Exemple x=7 est la solution de léquation 2x-3 = -x + 18
car :
Pour x=7 2x-3 = 2×7 3 = 14 3 = 11
-x + 18 = -7 + 18 = 11
Pour x = 7 on a 2x-3 = -x +
18 qui est vérifiée, x=7 est donc solution de cette équation
Une équation du premier degré
possède une solution unique lorsquelle
existe.
RESOLUTION DUNE EQUATION DU PREMIER
DEGRE
Pour résoudre une équation,
il faut isoler linconnue « x » dans lun des membres de légalité ( il faut que le « x » soit seul ). Pour le faire
on effectue les mêmes opérations sur les deux membres de légalité.
Exemples
x + 5 = 12
Pour
résoudre cette équation il faut « supprimer » le « +5 ».
Pour le faire on va soustraire 5 ( ou ajouter -5) aux
deux membres de légalité :
x+ 5 + (-5) = 12 + (-5)
Ensuite on fait les calculs
dans chaque membre :
x = 7
Léquation est résolue car le
« x » est isolé.
Vérification : Pour x = 7 : x+5 = 7 + 5 =
12 : légalité est vérifiée.
‚
3x + 8 = 4
Pour résoudre cette équation,
il faut « supprimer » le +8 en ajoutant (-8) aux deux membres puis
« supprimer » le 3 devant le x en divisant par 3 (
ou en multipliant par 1/3) les deux membres de légalité :
3x + 8 + (-8) = 4 + (-8)
Léquation devient :
3x = -4
On effectue ensuite la
seconde opération :
(1/3)×3x = -4 ×(1/3)
Ainsi x = -4/3 : Léquation est résolue.
ƒ
3x 8 = 4x 2
Dans ce type déquation,
linconnue « x » apparaît dans les deux membres de légalité. Il faut
donc dans un premier temps regrouper les x dans un des membres de légalité. Si
je choisis de les supprimer à droite, il faut supprimer 4x en ajoutant (-4x)
aux deux membres :
(-4x) + 3x 8 = 4x 2 + (-4x)
On obtient alors : -x 8 = - 2, la
résolution se termine en ajoutant 8 aux deux membres et en multipliant par
(-1). On trouve alors :
x = - 6.
F Exercice : En
vous inspirant de ces exemples faîtes les exercices suivants :
x - 2=8 x
- 5 = 60 x - 15 = -20
x - 12 = 13 x -8 = 8
2
x = 8 15 - x = 60 -5-x = -20 -13 - x = 13
Un problème posé
par une situation, notamment commerciale ou professionnelle ,
peut se traduire par une équation .
Pour résoudre un
problème, on doit respecter l'ordre de procédure suivant :
Choix de la ou des inconnues : après avoir lu et analysé l'énoncé,
choisir une inconnue.
Mise en équation : établir l'équation traduisant la situation
étudiée.
Résolution de équation , ou dun
système déquations du premier degré à 1 ou 2 inconnues .
Discussion du problème :
énoncer le résultat en rédigeant une phrase et vérifier si ce résultat est
conforme au problème posé .
Essayer de trouver la solution des exemples
suivants seul, si vous n'y parvenez pas regarder les étapes une à une.
Exemple n°1 : Un
rectangle a les caractéristiques suivantes :
Son périmètre
mesure 80 m ; sa longueur est le
triple de sa largeur .
Calculer
sa longueur et sa largeur .
Nommons "x" la largeur du rectangle . l = x
En fonction de "x" : la longueur du rectangle est L = 3x
Si on fait un
schéma :
Le périmètre est
donc égal en fonction de x à
P = 3x + x + 3x +
x = 8x
Equation à résoudre : 80 = 8 x
( on divise par 8 les deux membres)
on obtient
x = 10
La largeur du rectangle est de 10 m ; la longueur du rectangle est de
3 fois 10 m soit 30 m.
vérification : P rectangle = 2 ( L + l )
= 2 ( 30 + 10 ) = 2 ( 40) = 80
Exemple n°2 : Trouver 3 nombres entiers pairs
consécutifs dont la somme est égale à 36 . Donner la
valeur du premier nombre.
On choisi "x" le premier nombre .
Les deux autres nombres sont
"x + 2" et " (x+2)
+ 2 = x +4"
l'énoncé se traduit par l'équation : x + (x+2)
+ (x +4) = 36
soit x + x
+x +2 + 4 = 36 ; 3x + 6 = 36
Résolution de l'équation :
3x + 6 = 36 ; ( on ajoute -6 aux deux
membres)
3x + 6
- 6 = 36 - 6 ;
3x = 30
( on divise les deux membres par 3)
x = 10
Conclusion : le premier nombre
pair est " 10"
Le deuxième
nombre est 10 + 2 soit 12 ; le troisième
nombre est 12 + 2 = 14
vérification : 10
+ 12 + 14 est bien égal à 36 ; donc les trois nombres entiers pairs consécutifs
sont 10 ; 12 ; 14 .
Exemple n°3 : Un ouvrier met 15 minutes pour usiner une pièce.Pour
aménager et préparer le poste de travail en début de semaine,il
faut prévoir 3h 45 mn. Combien de pièces peut-il usiner sur une semaine de 35 heures ?
Prendre
"x" le nombre de pièces.( transformer la durée en nombre décimal)
L'inconnue "x" est le nombre de pièces usinées.
On met le temps sous forme décimale : 15 mn = 0, 25 h : 3h 45 = 3,75
h; 35 h ne change pas = 35 h
Mise en équation
: 0,25 x + 3,75 = 35
Résolution de l'équation :
0,25 x + 3,75 = 35
0,25 x = 35
- 3,75 (On ajoute -3,75 aux deux membres)
0,25 x =
31,25 ( on divise 31,25 par 0,25 )
x =![]()
x = 125
Le nombre de pièces usiner en une semaine sera de 125 pièces .
EXERCICES ET
PROBLEMES DAPPLICATION
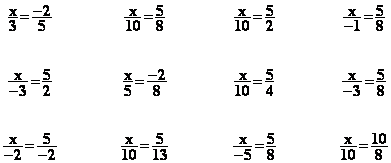
1°) Résoudre les équations
suivantes
1 x
= 7 5 x = 45 5+
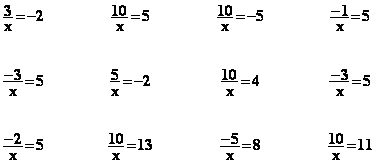
x = 45 5 - x = 45 x -5 = 45 ![]() =
= ![]()
![]() =
= ![]()
![]() =
=![]()
![]() =
=![]()
![]() = 8
= 8 ![]() =2
=2
4(x-7) = 32 7x-4 = 8x + 2 2(x-3) + 8x = 5( x 2)
Problèmes
+Consigne : Forcez vous à reprendre les 4 points
qui permettent de mettre un problème en équation même si la solution est
trouvable mentalement.
1°) Un rectangle
a les caractéristiques suivantes :
Son périmètre mesure
120 m ; sa longueur est le quadruple de sa largeur .
Calculer sa longueur et sa largeur .
2°) Trouver 3
nombres entiers pairs consécutifs dont la somme est égale à 36
. Donner la valeur du premier nombre.
3°) Une ouvrier
met 15 minutes pour usiner une pièce , pour aménager et préparer le poste de travail il
faut prévoir 3h 45 mn. Combien de pièces peut-il usiner sur une semaine de 35 heures ?
Prendre
"x" le nombre de pièces.
4°) Trouver trois nombres
entiers consécutifs dont la somme est 1884 .( prendre
pour inconnue , le plus petit nombre.
5°) Trouver 3
nombres multiples de 3
consécutifs dont la somme est 27
Prendre pour inconnue le plus
petit nombre .
6°) Trouver 5 nombres entiers
impairs consécutifs dont la somme est
75.
7°) Trouver 13 nombres consécutifs dont la somme est 2457 .
8°) Quel nombre faut-il
multiplier 34 pour obtenir 25 ?
Problèmes
supplémentaires
1°) Le réservoir d'une voiture est au deux cinquièmes rempli . Il faut
ajouter 38 litres de carburant pour le
remplir entièrement . Quelle est la contenance de ce
réservoir ?
2°) Le réservoir
d'un voiture est vide aux deux tiers . On
ajoute 30 litres de carburant pour le remplir aux trois quarts .
Quelle est la contenance du réservoir ?
3°) La largeur d'un
rectangle est le tiers de sa longueur et
le périmètre mesure 48 m . Calculer les dimensions de
ce rectangle . ( 6 et 18 m)
4°) La longueur d'un
rectangle surpasse de 10 m sa largeur . Le périmètre est de 120 m .Calculer les dimensions
de ce rectangle . ( 25 et 35
m)
5°) Le 1er janvier
1997 la population de la France a été estimée à 58 494 000 habitants se répartissent en 30 017 000 femmes et 28 477 000 hommes.
Quel pourcentage de la
population les femmes et les hommes représentent - ils
?
6°) Augmenter un nombre de x %
, c'est multiplier ce nombre par
( 1 + ![]() ) ou ( 1 + 0,01x )
) ou ( 1 + 0,01x )
Pour calculer le pourcentage d'augmentation du prix d'un objet qui passe
de 34 à 39,5 ,
on écrit : 39,5 = 34 ( 1 + 0,01 x)
Ecrire cette équation sous la
forme ax + b = c , puis la
résoudre ( arrondir à 0,01 près , ou à 2
décimales).
Enoncer le résultat sous
forme d'une phrase .
7°) Calculer le pourcentage
d'augmentation de la population d'un village qui passe de 3764 habitants à 3978 .
8°) Un centre de formation
organise un voyage .Le transporteur propose un prix global correspondant à 160
par personne . Si le nombre de personnes
augmente de 5 , on passe pour le même prix global , à 120 par personne.
Combien de personnes
participent au voyage ?
9°) La durée de fabrication d'une pièce est de
6,50 mn.
Au cours d'une journée de 8 h , combien peut-on fabriquer de pièces sachant qu'il faut
compter 1 h 30 mn pour le réglage la machine et l'affûtage de l'outil et
l'approvisionnement .
10°)
|
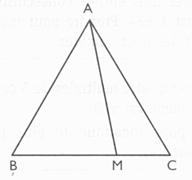
ABC est un triangle équilatéral de côté 6 cm On place sur le côté [BC] le point M tel que BM = d. 1°) Calculer la hauteur du triangle ABC ,
puis l'aire du triangle . 2°) Où doit -on placer le point M pour que l'aire
du triangle AMC soit égale à 10? |
|
11°)
|
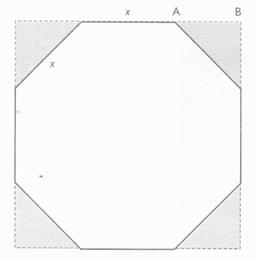
On veut découper dans une
plaque carrée de 0 cm de côté un octogone régulier de côté "x". a) Sachant que chaque triangle hachuré est un triangle
rectangle isocèle , déterminé la mesure de chacun de
leurs angles aigus . b) Calculer la longueur
AB en fonction de "x" , puis la
longueur "x". |
|
12°)
|
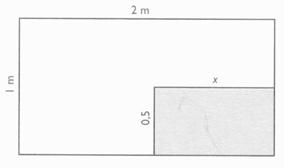
Dans une pièce
rectangulaire de 2 m de longueur et de 1 m de large ,
on effectue une découpe de forme rectangulaire comme l'indique la figure ci
-dessous. Donner l'expression de
l'aire de la partie restante en fonction de "x". Calculer "x" pour
que l'aire de la partie restante soit
1,25 m². |
|
|
13°)
|
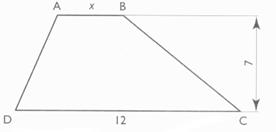
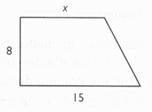
On considère un trapèze
ABCD. Vérifier que l'aire du
trapèze peut s'écrire :A = 8,5 x Calculer "x" pour
que l'aire du trapèze soit égale à 172,2 cm² ( arrondie
à deux décimales) |
|
14°)
|
Un triangle a les
dimensions ( en m) indiquées sur la figure . Exprimer le périmètre du
triangle en fonction de "x". Calculer "x" pour
que le périmètre soit égal à 30 m . En déduire les dimensions du triangle
. |
|
15°)
|
Montrer que l'expression de
l'aire du trapèze
rectangle en fonction de "x" est : A = 4 x + 60 Calculer "x" pour
que l'aire du trapèze rectangle soit égale à 200 cm² .
Pour cela , résoudre l'équation : 4x + 60 = 200 |
|
Représentation
graphique de deux grandeurs Equation de droite
Pour repérer un
point dans un plan, on utilise deux axes perpendiculaires sécants en O et
gradués de la même façon.
O est l'origine
du repère.
L'axe (OI)
horizontal munit du segment unitaire [OI] est appelé "axe des
abscisses"
On note également
cet axe (x'Ox) ( lire
"x prime O x").
L'axe vertical
(OJ) vertical munit du segment unitaire
[OJ] est appelé "axe des ordonnées".
On note également
cet axe (y'Oy) ( lire "
y prime O y" ).
Dans ce repère ( O,I,J ) du plan, chaque point M tel que « M » est repéré par ses
coordonnées :
·
son
abscisse notée : x M
·
son
ordonnée notée : y M .
(x M et y
M sont des nombres relatifs
).
On
notera : M (x M ;
y M)
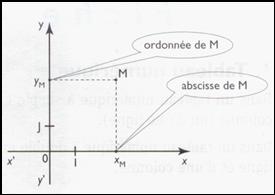
Les coordonnées dun point
dans un repère du plan sont des nombres relatifs ; ils peuvent
être positifs ou négatifs.
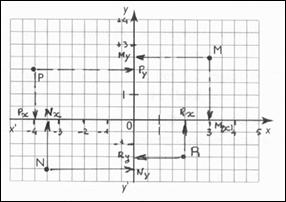
Exemple :
|
Points |
Abscisse |
Ordonnée |
Coordonnées |
|
M |
xM = + 3 |
yM = +2,5 |
M ( 3; 2,5) |
|
P |
xP = -4 |
yP = +2 |
P ( -4 ; +2 ) |
|
N |
xN = -3,5 |
yN = -2 |
N ( -3,5 ; -2) |
|
R |
xR = +2 |
yR =
-1,5 |
R ( 2 ; -1,5) |
Un plan peut être
divisé en quatre parties ou quadrants .
On identifie la
position d'un point dans un quadrant précis grâce aux signes des valeurs des
coordonnées de ce point :

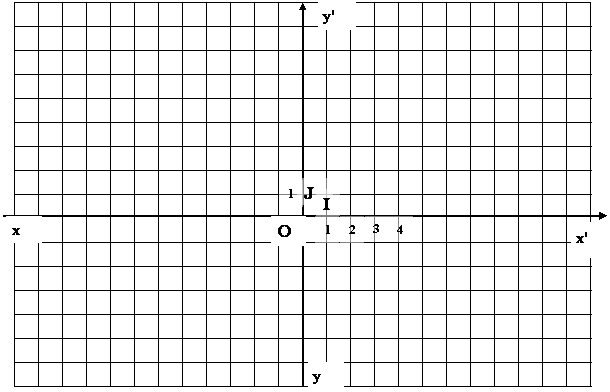
Placer
les points suivants dans le repère ci dessus :
A(
2; -2 ) B( 3 ; -3 ) C ( -1 ; 0 ) D
(-1 ; -1 ) E ( 4,5 ; 8) F (-3,5 ; -2 )
G (
4 ; -4 ) H( 2,5 ; -6,5 ) L
( -1,5 ; 3,5 ) M ( 1,25 ;
2) N ( 5 ; -5 )
REPRESENTATION GRAPHIQUE D'UNE GRANDEUR EN FONCTION
D'UNE AUTRE
Principe : Il s'agit de représenter dans un repère des points dont les
coordonnées sont constituées des valeurs prises par chacune des deux grandeurs.
Les
valeurs d'une des grandeurs constitueront les valeurs de l'abscisse de chaque
point et les valeurs correspondantes de l'autre grandeur constitueront les
valeurs de l'ordonnée de chaque point.
FExercice
|
Temps (min) |
1 |
2 |
3 |
4 |
5 |
|
Quantité d'eau (L) |
0,9 |
1,8 |
2,7 |
3,6 |
4,5 |
Ce tableau regroupe la
quantité d'eau exprimée en litre qui s'écoule d'un robinet en fonction du temps
exprimé en minutes
Représenter graphiquement les
deux grandeurs en prenant pour abscisse du point, le temps et pour ordonnée, la
quantité d'eau correspondante
Unités graphiques : Axe
des abscisses : 1 cm représente 1 min
Axe des ordonnées : 1 cm
représente 1 L
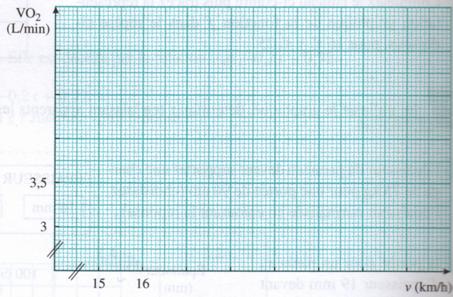
FExercice
Un test d'effort sur tapis
roulant permet de déterminer la consommation d'oxygène VO2 en litres
par minutes en fonction de la vitesse (km/h).
Les données sont regroupées
dans le tableau suivant :
|
V (km/h) |
15 |
16 |
17 |
18 |
19 |
20 |
|
VO2(L/min) |
2,9 |
3,2 |
3,5 |
3,8 |
4,1 |
4,4 |
Représenter ces deux
grandeurs dans le repère suivant :
+
FExercice
Dans une revue automobile, on
a relevé la courbe de freinage d'un Roadster :
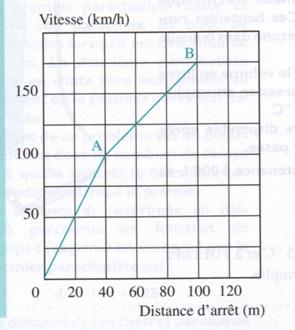
1°)
Quelle est la vitesse à ne pas dépasser pour s'arrêter en moins de 50 m.
2°)
Quelle est la distance de freinage à partir s'une vitesse de 40 km/h, 60 km/h,
160 km/h.
3°)
Compléter le tableau suivant :
|
V(km/h) |
|
100 |
|
|
125 |
150 |
|
Distance |
20 |
|
80 |
30 |
|
|
EQUATION DE DROITE
Dans
la plupart des exercices précédents, vous pouvez constater que la
représentation graphique de deux grandeurs est une droite. Lorsque tel est le
cas, il existe alors une relation entre labscisse x et lordonnée y des points
situés sur la droite. Cette relation est de la forme y = ax
+ b.
Déterminer
léquation dune droite, cest calculer les valeurs de a et b.
Le
coefficient a est appelé le coefficient directeur de la droite car cest ce
coefficient qui donne la direction de la droite. Le coefficient b est appelé lordonnée à
lorigine
car lorsque x=0 dans y=ax+b on retrouve y = b.
Méthode de calcul de a et b
Les
formules qui permettent de calculer a et b seront
démontrées dans les paragraphes suivants.
Si
une droite passe par A(xA ;yA) et B(xB ;yB) alors on a :
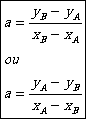 et
et
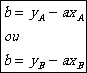
Exemple : Quelle est léquation
de la droite passant par les points A(2 ; 3 ) et
B( -1 ; 5 ) ?
En
appliquant les formules : 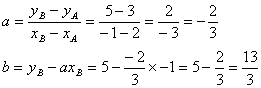
Léquation
de la droite (AB) est ![]()
Vérification : les coordonnées de A
et B doivent vérifier cette relation, en remplaçant x dans léquation o doit
retrouver la valeur de y pour chacun des deux points.
Pour
A : ![]() , pour x = 2 on
retrouve bien y = 3
, pour x = 2 on
retrouve bien y = 3
Pour
B : ![]() , pour x = -1 on
retrouve bien y = 5
, pour x = -1 on
retrouve bien y = 5
Pour
représenter graphiquement cette droite on place les points A er B dans un repère et on trace la droite :
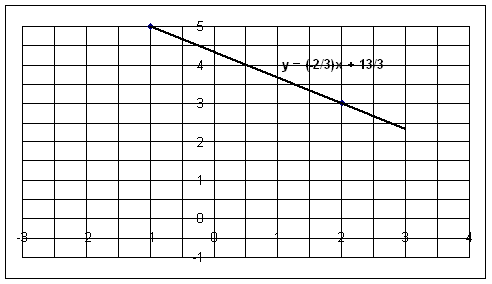
Pour
tracer sur un graphique une droite dont on connaît léquation, il suffit
dutiliser léquation de cette droite pour calculer les coordonnées de deux
points.
FExercices
1°)
Déterminer léquation des droites passant par les points suivants :
o A( 5 ; 3 ) B(-1 ; -2 )
o C(1/2 ; -2/3) D(0 ; 1)
o E(0 ;0) F(-2/5 ; 6)
2°)
Dans un repère ayant pour unités graphiques 1 carreau pour 1 unité en abscisse,
1 carreau pour 1 unité en ordonnées et pour -10 < x < 10
, -10 < y < 10 Tracer le droites déquations suivantes :
D1 : y = 2x D2 : y = -x + 8 D3 : y = 5x -2 D4 : 2y +3x -3
= 0
A retenir :
o
Deux droites dont les coefficients directeurs sont
égaux sont parallèles
o
Deux droites dont le produit des coefficients
directeurs est égal -1 sont
perpendiculaires.
o
RESOLUTION DUN SYSTEME DE DEUX EQUATIONS A DEUX
INCONNUES
Dans ce cours est présenté
trois méthodes de résolution d'un système de deux d'équations à deux inconnues.
En général on note x et y les
inconnues.
Un système d'équation sert à
résoudre des problèmes du premier degré dans lesquels deux solutions sont à
déterminer.
Résoudre le système
d'équation d'inconnues x et y suivant : 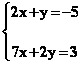 (par exemple) consiste à trouver les valeurs de x et y qui
soient solutions des deux équations du
système en même temps. La solution du système est notée (
valeur de x ; valeur de y )
(par exemple) consiste à trouver les valeurs de x et y qui
soient solutions des deux équations du
système en même temps. La solution du système est notée (
valeur de x ; valeur de y )
Il existe (entre autres)
quatre méthodes de résolution :
§
Méthode dite de
"substitution"
§
Méthode dite de
"combinaison"
§
Méthode des
déterminants
§
Méthode dite
"graphique"
METHODE DE
SUBSTITUTION
Reprenons l'exemple précédent
:
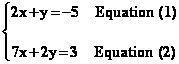
Cette méthode consiste à
exprimer à l'aide de l'équation(1) y en fonction de x
et de remplacer y par son expression en fonction de x dans l'équation(2). On
ramène ainsi l'équation (2) à une équation du premier degré d'inconnue x que
l'on peut résoudre.
Transformation de l'équation(1)
:
2x + y = -5 ð y = - 5 - 2x Equation(1)
Remplacement de l'équation(1)
dans l'équation(2) et résolution de l'équation (2)
7x + 2 (-5 - 2x ) = 3
7x -10 - 4x = 3
3x - 10 = 3 donc ![]()
Remplacement de la valeur de x trouvée dans l'Equation(1) transformée
![]() ¯
¯
La solution du système est : ![]()
Vérification de la solution
Vérification pour
l'équation (1) : ![]()
L'équation (1) est vérifiée
pour ![]()
Vérification pour
l'équation (2) : ![]()
L'équation(2) est vérifiée pour ![]()
La solution du système 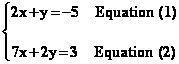 est :
est : ![]()
METHODE DE
COMBINAISON
Cette méthode consiste à
multiplier les équations par des nombres choisis de manière à ce que les
coefficients d'une inconnue soient opposés, puis on additionne membre à membre
les deux équations obtenues. On obtient ainsi une équation du premier degré à
une inconnue que l'on résout pour trouver la valeur d'une inconnue.
Avec le système choisis au
départ : 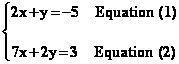
On choisit de déterminer x , on veut éliminer y en additionnant membre à membre les
deux équations pour cela on multiplie l'équation (1) par (-2)
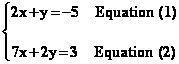 ð
ð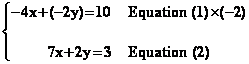
On additionne les deux
équations précédentes membre à membre, puis on résout l'équation en x :
-4x + (-2y) + 7x + 2y = 10 + 3
3x = 13
![]()
Pour déterminer la valeur de
y on remplace x par ![]() dans une des deux équations.
dans une des deux équations.
Par exemple l'équation (1) : ![]() donc :
donc : ![]() La solution de ce système est donc :
La solution de ce système est donc : ![]()
METHODE DES
DETERMINANTS
Exemple : 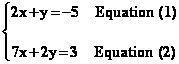
·
On calcule le
déterminant principal D, il est constitué des coefficients devant x et y écris
en colonne tels quils se présentent dans le systèmes.
Pour calculer la valeur de ce déterminant, on fait un produit en crois et on
soustrait les deux valeus (
toujours en commençant par la gauche ):
·
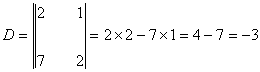
·
On calcule
ensuite le déterminant de x, Dx ,
on remplace les coefficients devant x dans D par les seconds membres :
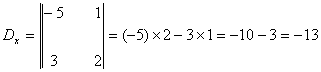
Ensuite
on calcule x de la façon suivante :
![]()
·
On calcule le
déterminant de y, Dy, on remplace dans D
les coefficients de y par les seconds membres, le principe de calcul est le
même :
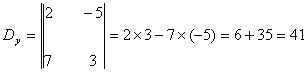
Ainsi ![]()
Ainsi la solution du système
est : ![]() .
.
METHODE GRAPHIQUE
On considère dans cette
méthode les deux équations comme deux équations de droites.
Soit le système : 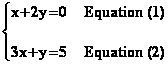
On écrit ensuite les deux
équation de ce système sous la forme plus classique d'une équation de droite ( de la forme y = ax + b )
Ce système devient : 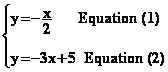
On trace ensuite ces deux
droites dans un repère convenablement choisi :
La droite d'équation (1)
passe par les points de coordonnées (0 ; 0 ) et (4 ;
-2 )
La droite d'équation (2)
passe par les points de coordonnées (0 ; 5 ) et ( 3 ;
-4 )
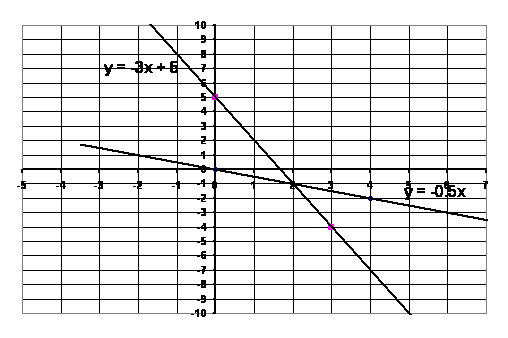 Les
coordonnées du point d'intersection des 2 droites donne ainsi la solution du
système d'équation soit
Les
coordonnées du point d'intersection des 2 droites donne ainsi la solution du
système d'équation soit
(2 ; -1
)
Vérification : Equation (1)
: 2 + 2´(-1) = 2 -2 = 0
Equation (2) : 3´2 + (-1) = 6 - 1 = 5
FExercices
1°)Résoudre
les systèmes suivants par substitution ou combinaison :

2°)Résoudre
par la méthode des déterminants les systèmes suivants

3°)Pour
un concert de Jazz, les places valent 7 ou 13 .
Une association a acheté 32
places pour un montant total de 272
Combien de places de chaque
sorte l'association a t-elle acheté ?
4°)Pour
se rendre d'une ville A a une ville B, un
automobiliste emprunte successivement l'autoroute et la route.
La distance totale parcourue
est de 450 km.
La vitesse moyenne sur autoroute
est de 120 km/h ; la vitesse moyenne sur route est de 80 km/h.
Le trajet total s'effectue en
4 heures.
a) On désigne par x la distance parcourue en km
sur autoroute. Montrer que la durée t1 ( en
heure) du parcours sur autoroute est donnée par :
![]()
On rappelle que la distance d parcourue
pendant le temps t à une vitesse moyenne v est donnée par la relation :
d
=vt
b)
On désigne par y la distance parcourue en km sur route. Déterminer l'expression
de la durée t2 ( en heures) du parcours sur
route.
c)
Résoudre le système : 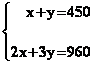
En déduire les distances
parcourues sur la route et sur l'autoroute par l'automobiliste.
Les inéquations
INEQUATIONS
A UNE INCONNUE DU PREMIER DEGRE
Définition
Une
inéquation est une relation d'ordre mathématique qui comprend une inconnue en
général notée x. Elle comprend les sigles suivants :
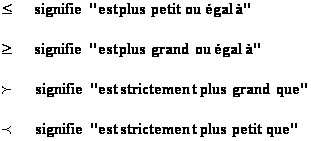
Elle
est du premier degré lorsque la puissance de x ne dépasse pas 1
|
4x - 1 |
> |
x + 2 |
|
premier |
|
second |
Exemple :
Résoudre
une inéquation, c'est trouver toutes
les valeurs de l'inconnue pour que l'inéquation soit vérifiée.
Ces valeurs sont les solutions de l'inéquation.
Exemple
·
Si x = 0, alors
le premier membre vaut: 4 * 0 - 1 = 0 - 1 = -1
et le second membre vaut: 0 + 2 = 2.
Comme -1 > 2 est faux, alors 0 n'est pas solution de l'inéquation.
·
Si x = 3, alors
le premier membre vaut: 4 * 3 - 1 = 12 - 1 = 11
et le second membre vaut: 3 + 2 = 5.
Comme 11 > 5 est vrai, alors 3 est une solution de l'inéquation.
On
remarque qu'il y a une infinité de solutions possibles. On parlera donc d'ensemble
de solutions.
Pour
trouver les solutions d'une inéquation, la méthode suivante est utilisée.
· Méthode de résolution
Objectif : "Isoler x" dans un membre (généralement le premier
membre).
Procédé : Transformer l'inéquation à l'aide des règles 1 ,2 et 3 énumérées ci après.
Une
inéquation a les mêmes solutions que toutes les inéquations obtenues:
·
R1: En ajoutant ou en retranchant un même nombre aux deux
membres de l'inéquation:
Si a < b
alors a + c < b + c (ex: a + 5 < b + 5)
alors
a - c < b - c (ex: a - 5 < b - 5)
·
R2: En multipliant ou en divisant par un même nombre
positif non nul les deux membres de l'inéquation:
Si a > b et c
> 0 alors a * c > b *
c (ex: a * 3 > b * 3)
alors
a / c > b / c (ex: a / 3 > b / 3)
·
R3: En multipliant ou en divisant par un même nombre
négatif non nul les deux membres de l'inéquation et en changeant
le sens de l'inégalité:
Si a > b et c <
0 alors a * c < b *
c (ex: a * (-4) < b * (-4))
alors
a / c < b / c (ex: a / (-4) < b / (-4))
Exemple :
Résoudre l'inéquation : 4x - 1 > x + 2
On
regroupe les "termes en x" dans le premier membre à l'aide de R1:
(on retranche x)
4x - 1 - x > x + 2 - x
On réduit : 3x - 1 >
2
On
regroupe les "termes sans x" dans le second membre à l'aide de R1:
(on ajoute 1)
3x - 1 + 1 > 2 + 1
On réduit :
3x >
3
On
"isole x" à l'aide de R2: (on divise par 3 dans les deux membres)
3x / 3 > 3 / 3
On réduit : x >
1
Les solutions sont tous les nombres strictement plus
grand que 1.
On
note également l'ensemble des solutions sous la forme d'un intervalle dans ce
cas cet intervalle est : ] 1 ; + ¥ [ ( "+ ¥ " se lit "plus l'infini", ce sont tous
les nombres positifs très grands ).
* Précisions
sur la notations des intervalles de nombres :