LES EQUATIONS ET POLYNOMES DU SECOND DEGRE

Une équation du second degré est une équation de la forme :

ax²+bx+c = 0 avec a,b,c nombre réels.

Exemple : 2x² -3x + 2 = 0.

RESOLUTION D'UNE EQUATION DU SECOND DEGRE

Résoudre une équation du second degré consiste à trouver les valeurs de x(on les appelle les solutions ou racines de l'équation) qui vérifient l'équation : qx²+bx+c = 0 où a ¹ 0.

Vous admettrez la démarche suivante pour effectuer la résolution de cette équation :

1^ere étape : On calcule D = b²-4ac (D qui se lit "delta" est appelé le discriminant)

2^emeétape :

ŒSi D < 0 alors l'équation n'a pas de solutions

�Si D > 0 alors l'équation admet deux solution x₁ et x₂ qui se calculent à l'aide des formules :

¸

Ž Si D = 0 alors l'équation admet une solution x₁. x₁ se calcule à l'aide de la formule :

Exemple On veut résoudre l'équation 2x² - 5x -3 = 0

1^ere étape : Dans ce cas : a = 2 ; b = -5 et c = -3

On calcule D = b²-4ac = 5² - 4´2´(-3) = 25 + 24 = 49

2^emeétape : D > 0 on calcule donc les deux solutions x₁ et x₂ :

Vérification : Pour vérifier les calculs il suffit de remplacer x par les valeurs de x₁ puis x₂ :

2 ´ 3² - 5 ´ 3 -3 = 18 - 15 - 3 = 0 donc 3 est bien une solution de l'équation 2x² - 5x -3 = 0

2 ´ (-1/2)² - 5 ´ (-1/2) -3 = 2/4 + 5/2 -3 = 0 donc -1/2 est bien une solution de l'équation 2x² - 5x -3 = 0

FExercice n°1

Donner les solutions exactes puis arrondies à 0,1 près lorsque cela est possible des équations suivantes :

a) 3x²+2x-1=0 b) 16x²+40x+25=0 c) -2x+x-1=0 d) .2x²+3x-4=0

e) x²-2x=5 f) 2x²=3x-2 g) -3x²=2-x h) 2x² = 3x² - 8x + 3

FACTORISATION D'UN POLYNOME DU SECOND DEGRE

La factorisation d'un polynôme du second degré de la forme ax²+ bx + c dépend du nombre de solutions de l'équation du second degré ax² +bx + c = 0 :

Si D > 0 alors l'équation admet deux solution x₁ et x₂ et le polynôme se factorise de la manière suivante :

Si D = 0 alors l'équation admet une solution x₁ et le polynôme se factorise de la manière suivante :

Si D < 0 alors l'équation n'a pas de solutions et le polynôme ne peut pas se factoriser.

FExercice n°2

Pour les équations de l'exercice n°1, donner la factorisation de chaque polynôme lorsque cela est possible.

Application de la factorisation

On utilise la factorisation du polynôme du second degré afin d'étudier son signe. Faisons cette étude à l'aide d'un exemple :

Soit le polynôme 4x² - 7x - 2.

Œ Résoudre l'équation : 4x² - 7x - 2=0

� Factoriser le polynôme 4x² - 7x - 2.

ŽRésoudre les inéquations x + 0,25 > 0 et x - 2 > 0

�Reproduire et, en utilisant les résultats précédents, compléter le tableau suivant :

x	-0,25 2
Signe de x + 0,25	0
Signe de x-2	0
Signe de 4x² - 7x - 2	0 0

Généralisation : Signe du polynôme ax²+bx+c

Œ Si D > 0, alors ax²+bx +c est du signe de a sauf entre les solutions x₁ et x₂

� Si D 0, alors ax²+bx+c est toujours du signe de a

On se sert du signe du polynôme pour résoudre des inéquation du second de gré

FExercice n°3

On considère le polynôme P(x) = 16x² + 40x + 25.

1. Résoudre l'équation 16x² + 40x +25 = 0

2. Faire le tableau de signe du polynôme, en déduire l’ensemble des solutions de P(x)<0

REPRESENTATION GRAPHIQUE

La représentation graphique de y=ax² + bx + c ( avec a ¹0) consiste à placer des points de coordonnées M(x ; y) dans un repère orthogonal.

Exemple : Pour 2x²-3x+2. On fait un tableau de valeurs :

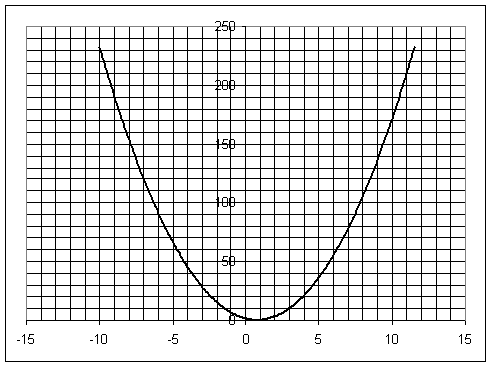
La représentation graphique est une parabole.

Remarque : si a est positif alors le sommet de la parabole est en bas. Lorsque a est négatif, le sommet de l parabole est en haut.

EXERCICES D'APPLICATION

1°) Pour chacune des équations suivantes :

v Indiquer les valeurs de a, b et c et calculer le discriminant.

v En déduire le nombre de solutions de l'équation

x² + 9x + 19 = 0 x² - 4x + 4 = 0 -3x² + x - 2 = 0 4x² + 5x - 6 = 0

2°) Résoudre les équations proposées :

x² + x - 6 = 0 x² - 6x + 9 = 0 4x² - 5x - 6 = 0 x² - x + 1 = 0

9x² + 6x + 2 = 0 -2x² - 13x + 7 = 0 4x² + 12 x + 9 =0 12x² = 5x +2

3°) Factoriser quand cela est possible les polynômes suivants :

x²+2x-3 4x²+5x-6 -2x²+5x-3 3x²+2x+2

4°) Pour chaque polynôme proposé :

Donner la factorisation

Etudier à l'aide d'un tableau de signe le signe du polynôme.

4x² + 3x - 1 3x² - 4x + 4/3 x² - 3x + 2 -2x² + 3x - 2

5°) Résoudre les inéquations suivantes : 15x² - 17x - 4 < 0 et 9x² - 12x + 4 ³ 0

6°) Résoudre les inéquations suivantes : x²-2x 8 et x(x+6)>21+2x

7°) Déterminer la valeur de la résistance x pour que les montages ci-dessous soient équivalents :

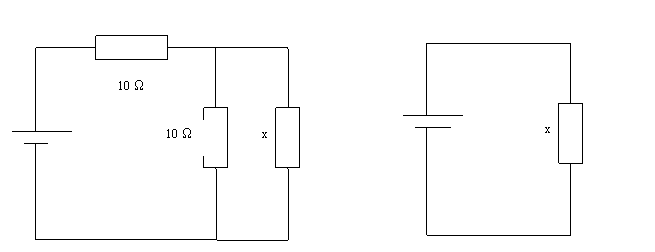
8°) La courbe C est la courbe représentative de la fonction f définie sur l'ensemble des réels par

f(x) = -x² + 3x

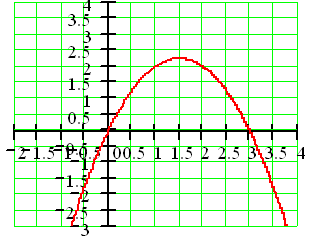
a) Résoudre graphiquement l'équation -x² + 3x = 0

b) En utilisant le graphique indiquer le nombre de solutions des équations f(x) = 1 f(x) = 2,25 f(x) = 4

c) En utilisant les formules de résolution, résoudre les équations :

-x² + 3x = 4 -x² + 3x = 2,25 -x² + 3x = 1

NB : on donnera les valeurs exactes des solutions puis les valeurs arrondies au centième.

9°) La distance de freinage d’un véhicule est imposée par une circulaire officielle.

Elle est donnée pr l formule suivante :

où

d est la distance de freinage en mètres,

v la vitesse du véhicule en début de freinage en km/h,

f le coefficient de frottement des pneus sur la route dans les conditions normales ( route sèche). f=0,4,

a est la pente de la route ; dans le cas d’une montée a>0 ( si la pente est de 10% alors a = 0,1) dans le cas d’une route horizontale a=0, dans le cas d’une descente a<0 (si la pente est de 5% alors a=-0,05)

Le coefficient 0,55 est le temps de réaction de l’automobiliste.

a. Calculer la distance de freinage pour v=130 km/h dans les cas suivants :

i. Sur une route horizontale

ii. Sur une montée de 6%

iii. Sur une descente de 6%

b. Calculer la vitesse à ne pas dépasser pour s’arrêter sur 100 m dans une descente de 8%

10°) Deux villages A et B sont distants de 60 km. Vous allez de A à B à la vitesse v ( en km/h) et vous revenez de Bà A à la vitesse v+15. Le temps de parcours est de 6 h. Quelle votre vitesse v ?