CORRECTION DE l’ EXERCICE 1 SUR LES INEQUATIONS
Exercice n°1
1°) Pour
répondre à cette question, on fait un tableau regroupant pour chaque type
d'objet les coûts de main d'œuvre et de matière première :
|
Objet |
Production
journalière |
Dépense
journalière en main d'œuvre |
Dépense
journalière en matière première |
|
A |
x |
125 x |
30 x |
|
B |
y |
75 y |
70 y |
|
Totaux |
x+y |
125 x + 75 y |
30 x + 70 y |
La dépense journalière
en main d'œuvre ne doit pas dépasser 1 250 €, ceci se traduit par l'inéquation
:
![]()
On peut
diviser les deux membres de cette inéquation par 25 on aboutit à :
![]()
La dépense journalière
en matière première ne doit pas dépasser 560 €, ceci se traduit par
l'inéquation :
![]()
On peut
diviser les deux membres de cette inéquation par 10 on aboutit à :
![]()
Pour satisfaire
aux contraintes journalières les quantités produites x et y doivent satisfaire
au système d'inéquation :
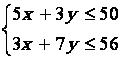
2°) Deux
conditions viennent se rajouter au système précédents on doit avoir évidemment ![]() car le nombre de pièces de chaque type produit doit être
positifs.
car le nombre de pièces de chaque type produit doit être
positifs.
Pour
répondre au problème il faut donc résoudre le système d'inéquation :
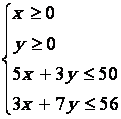
Il faut
transformer les deux dernières inéquations de façon à isoler y dans un membre,
le système devient alors:
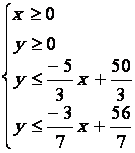
La zone
graphique solution de ce système doit être située :
Au dessus de l'axe des abscisses
A droite de