PREMIÈRE
PARTIE (12 points)
À traiter obligatoirement
Exercice 1 :
Effectuer les calculs suivants
en donnant les détails :
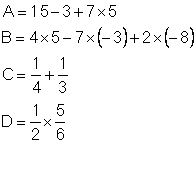
Exercice 2 :
Les puissances de 10 et
la notation scientifique sont utilisées pour l’écriture des grands et des
petits nombres, notamment en sciences. Voici quelques exemples :
|
|
Vitesse de la lumière en km/s |
Taille d’un atome en m |
Pression atmosphérique en hectopascal |
|
Notation scientifique |
3 |
|
1,013 |
|
Écriture décimale |
|
0,0000000009 |
|
Recopier puis compléter ce tableau sur la copie.
Exercice 3 :
Un
participant au marathon a mis 3 h 10 min 4 s pour parcourir 42,195 km.
a) Exprimer la durée en seconde.
b) Exprimer la
distance en mètre.
c) Calculer la
vitesse moyenne en m/s sachant que v = . Arrondir à 0,1.
d) Convertir le
résultat précédent en km/h.
Exercice 4 :
Résoudre
les équations suivantes :
a) ![]() 4 x – 3= 10
4 x – 3= 10
b) 7 x – 4 = 2 x + 6
c) =
DEUXIÈME
PARTIE (12 points)
Le
candidat traitera au choix la
partie A ou la partie
B
PARTIE A
STATISTIQUES
Exercice 1 :
À
la suite du recensement, l’INSEE propose plusieurs études. Dans une petite commune
de campagne, l’étude sur les milieux sociaux culturels des plus de 15 ans
permet d’établir le tableau de l’annexe 1.
a) Compléter
le tableau de l’annexe 1 (à remettre avec la copie).
Les
valeurs des fréquences seront arrondies au dixième.
b) Représenter cette série statistique par un
diagramme circulaire sur l’annexe 1.
c) Quel est le pourcentage des plus
de quinze ans de cette commune qui ont un emploi ? Arrondir au dixième.
Exercice 2 :
Le
responsable d’un organisme de vente de matériel informatique sur internet a relevé les montants des
commandes (en euro) passées par les internautes.
Les résultats sont donnés à
l’aide du diagramme suivant :
Nombre de commandes
Montant des commandes (€)
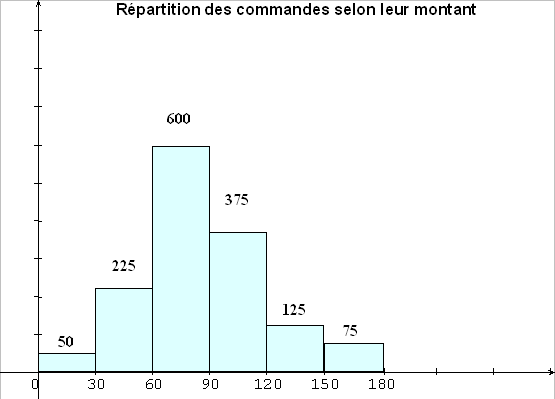
Compléter
le tableau de l’annexe 2 (à remettre avec la copie).
Répondre aux questions a) b) et c) de cette annexe.
PARTIE B
GÉOMÉTRIE
Exercice 1 :
Pour chacun des 4 cas ci-dessous,
indiquer une transformation géométrique qui permet de passer de la figure 1 à
la figure 2 (symétrie centrale, symétrie axiale, translation ou rotation).
Répondre
sur la copie.
|
1 2 |
|
1 2 |
|
1 2 |
|
1 2 |
||||||||||
|
|
|
|
|
|
|
|
I II III IV
Exercice 2 :
1) a) À l’aide du matériel de votre choix, tracer
sur la copie :
- un segment BC mesurant 8 cm,
- un segment
[AB] perpendiculaire à [BC] tel que AB = 4 cm,
- la droite ![]() parallèle à [BC]
passant par A.
parallèle à [BC]
passant par A.
b)
Placer le point D sur la droite![]() tel que l'angle
mesure 70°.
tel que l'angle
mesure 70°.
2) Mesurer AD.
3) Quel est le nom précis de la figure ABCD
obtenue ?
4) Calculer, en cm2, l’aire du
quadrilatère ABCD.
On
rappelle : aire = ![]()
 Exercice 3 :
Exercice 3 :
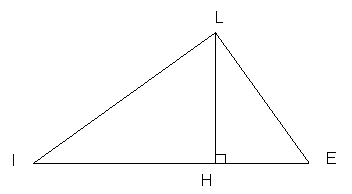
Soit
le triangle ILE représenté ci-contre
(la figure n’est pas à
l’échelle)
On
donne :
IE = 8 cm
IL = 7 cm
LE = 5 cm
1) Que représente
le segment [LH] pour le triangle ILE ?
2) Le triangle ILE
est-il rectangle ? Justifier par un calcul.
3) On donne : = 60°. En utilisant la formule
du sinus dans le triangle rectangle LHE, calculer, en cm, la longueur LH.
Arrondir à 0,01.
4) Calculer, en cm, la longueur IH en utilisant le théorème
de Pythagore dans le triangle rectangle LHI. Arrondir au dixième.
En
déduire HE.
TROISIÈME
PARTIE (12 points)
À traiter obligatoirement
Un véhicule consomme, en moyenne, 5 litres d’essence
aux 100 km. Le réservoir plein contient 50 litres.
1) a) Un
automobiliste part avec un réservoir plein. Quel volume d’essence a-t-il
consommé au bout de 200 km ?
b) Quel
volume d’essence reste-t-il dans son réservoir ?
2) Quel volume
d’essence reste-il au bout de 600 km ?
3) Au bout de
combien de km le réservoir sera-t-il vide ?
4) Le voyant du témoin d’essence s’allume lorsqu’il reste du plein d’essence dans le réservoir.
a) Calculer la quantité d’essence restant
dans le réservoir lorsque le voyant s’allume.
b) Quelle est alors la distance parcourue
par le véhicule ?
c) Quelle distance maximale le véhicule
peut-il encore alors parcourir ? (justifier la réponse)
5) Exprimer le
volume d’essence y (en litre) restant dans le réservoir quand
l’automobiliste a parcouru x km. (Le volume d’essence qui reste dans le réservoir
est égal au volume initial de 50 litres moins la quantité consommée).
6) Soit f la fonction définie par f (x) = 50 – 0,05 x pour x appartenant à l’intervalle
[0 ;
1 000].
a) Compléter le tableau de l’annexe 3 (à
remettre avec la copie).
b) La fonction f est-elle
affine ou linéaire ? Justifier la réponse.
c) Représenter graphiquement la fonction f dans le repère de l’annexe 3.
7) En vous aidant de la représentation graphique
précédente, lire la valeur de f (x) lorsque x = 900 (laisser les tracés apparents).
Que représente cette valeur pour ce problème de consommation
d’essence ?
ANNEXE 1
(à remettre avec la
copie)
a) Tableau :
|
Catégorie socioprofessionnelle |
Nombre de personnes |
Fréquence en pourcentage |
Angle (en degré) Mesure arrondie à l’unité |
|
Agriculteurs exploitants |
44 |
1,9 |
7 |
|
Artisans, commerçants, chefs d’entreprises |
84 |
3,6 |
13 |
|
Cadres et professions intellectuelles sup. |
47 |
2,0 |
|
|
Professions intermédiaires |
152 |
|
|
|
Employés |
256 |
|
40 |
|
Ouvriers |
496 |
|
|
|
Retraités |
576 |
|
|
|
Sans activité professionnelle |
656 |
|
|
|
Total |
|
100 |
360 |
b) Diagramme
circulaire :

ANNEXE 2
(à
remettre avec la copie)
Tableau :
répartition des commandes selon leur montant
|
Montant des commandes en
euro |
Nombre de commandes ni |
Centre de classes xi |
Produits ni ´ xi |
|
[ 0 ; 30 [ |
|
|
|
|
[ 30 ; 60 [ |
|
|
|
|
[ 60 ; 90 [ |
|
|
|
|
[ 90 ; 120 [ |
|
|
|
|
[ 120 ; 150 [ |
|
|
|
|
[ 150 ; 180 ] |
|
|
|
|
TOTAL |
1
450 |
|
|
a) Quel est le
nombre de commandes inférieures à 60 € ?
....................................................................................................................................................................
b) Quel est le
nombre de commandes d’au moins 90 € ?
....................................................................................................................................................................
c) Calculer le
montant moyen des commandes (arrondir au centième).
....................................................................................................................................................................
ANNEXE 3
(à
remettre avec la copie)
|
x |
0 |
100 |
200 |
1 000 |
|
f
(x) |
|
45 |
|
|