1) Une table de salon
circulaire a un rayon de 32 cm. Quelle est son aire ?
2) On veut couvrir un puits
circulaire de 55 cm de rayon avec une plaque métallique qui devra dépasser le bord
du puits de 5 cm. Quelle sera l’aire de cette plaque ?
3) Pour décorer une petite
table ronde de 50 cm de diamètre, maman confectionne un napperon d’un diamètre
inférieur de 15 cm à celui de la table. Quelle est l’aire du napperon ?
4) Une pelouse circulaire a
47,10 m de périmètre. Calculer son aire.
5) Sur le mur d’un collège, un
artisan réalise une mosaïque circulaire de 6 m de diamètre. Il est payé 329 € par m² posé. A combien revient la pose de
cette mosaïque ?
6) Pour confectionner un
dessous-de-plat, papa découpe, dans une planche carrée de 22 cm de côté, un
disque qui touche les 4 côtés de la planche. Quelle est l’aire du
dessous-de-plat ? Quelle est l’aire de planche inutilisée ?
7) Un disque de 33 tours a un
diamètre de 30 cm. Le trou central a 7 mm de diamètre. Calculer l’aire de la
surface pleine (au mm² près).
8) Un massif de fleurs a la
forme d’un disque de 6,50 m de diamètre. Le jardinier doit y planter des
rosiers et il estime qu’il faut environ 0,15 m² pour chaque plant. Combien de
rosiers faudra-t-il prévoir ?
9) Un couple a racheté un
vieux moulin et entreprend sa restauration. Le moulin, de forme cylindrique,
mesure 6,4 m de diamètre intérieur et comprend deux pièces superposées. Pour
repeindre les plafonds avec deux couches de peinture, combien de pots de 2,5 l
seront nécessaires si un pot couvre 35 m² ?
10)
Une table ronde de 1,10 m de diamètre est utilisée pour un repas de
famille. On lui ajoute, au milieu, deux rallonges rectangulaires mesurant
chacune 0,40 m sur 1,10 m. Quelle est l’aire totale obtenue ?
11)
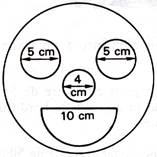Un enfant a réalisé en peinture un dessin
représenté par la figure ci-dessous. Le visage, d’un diamètre de 20 cm, est
peint en rose, le nez et la bouche en rouge ; les yeux sont laissés
blancs. Calculer les aires des surfaces roses, rouges et blanches.
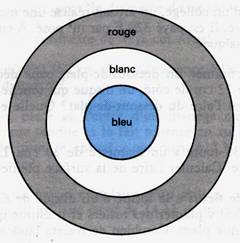
12)
Afin d’illustrer une leçon d’éducation civique, des élèves représentent
une cocarde tricolore (bleu, blanc, rouge) ; les diamètres des trois
cercles sont les suivants : 5 cm, 10 cm et 15 cm. Calculer les aires des
surfaces coloriées en bleu, en blanc, en rouge.
