Correction des
exercices du cours sur les équations et polynômes du second degré
Exercice
n°1
a)
![]() b)
b) ![]() c)
c) 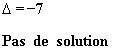 d)
d) 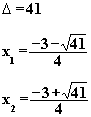 e)
e) 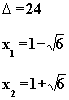
f)
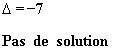 g)
g) h)
h)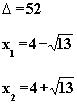
Exercice
n°2
a)
![]() b)
b) ![]() c) pas de
factorisations d)
c) pas de
factorisations d) ![]()
e)
![]() f)
f) ![]() g) Pas de factorisations h)
g) Pas de factorisations h)
![]()
Exercice
n°3
1°)
![]() il existe une solution :
il existe une solution : ![]()
2°) ![]() , P(x) est toujours positif.
, P(x) est toujours positif.
Corrigé des EXERCICES
D'APPLICATION
1°)
x²+9x+19=0 a=1 b=9 c=19 ![]() donc 2 solutions
donc 2 solutions
x²-4x+4=0
a=1 b=-4 c=4 ![]() donc une solution
donc une solution
-3x²+x-2=0 a=-3 b=1 c=-2 ![]() donc pas de solutions
donc pas de solutions
4x²+5x-6=0 a=4 b=5 c=-6 ![]() donc 2 solutions
donc 2 solutions
2°)
x² +x -6 =0 les solutions sont : -3 et 2 x²-6x+9=0
une solution x = 3
4x²-5x-6=0
les solutions sont 2 et -3/4 x²-x+1=0
pas de solution
9x²+6x+2=0
Pas de solution -2x²-13x+7=0
les solutions sont -7 et 1/2
4x²+12x+9=0
une solution -3/2 12x²=5x+2 les solutions sont -1/4 et 2/3
3°)
Pour factoriser un polynôme, il faut que celui-ci admette des racines :
x²+2x-3
= (x-1)(x+3) 4x²+5x-6=4(x-3/4)(x+2) -2x²+5x-3=-2(x-1)(x-3/2)
3x²+2x+2
n'est pas factorisable.
|
Valeurs de x |
-1 1/4 |
|
Signe de x+1 |
- 0 + |
|
Signe de x-1/4 |
- 0 + |
|
Signe de (x+1)(x-1/4) |
- 0
- 0 + |
|
Signe de P(x) |
+
0 - 0
+ |
4°)
4x²+3x-1=4(x-1/4)(x+1)
3x²-4x+4/3
= 3(x-2/3)² Ce polynôme est
toujours positif.
X²-3x+1
= (x-1)(x-2)
|
Valeurs de x |
1 2 |
|
Signe de x-1 |
- 0 + |
|
Signe de x-2 |
- 0 + |
|
Signe de (x-1)(x-2) |
+
0 - 0
+ |
|
Signe de x²-3x+1 |
+ 0 -
0 + |
-2x²+3x-2
Pas de solution, le polynôme est du signe de a c'est à dire négatif.
5°)
Résolution de 15x²-17x-4 < 0
On
fait un tableau de signe car : 15x²-17x-4 = 15(x+1/5)(x-4/3)
|
Valeurs de x |
-1/5 4/3 |
|
Signe de x+1/5 |
- 0 + |
|
Signe de x-4/3 |
- 0 + |
|
Signe de (x+1/5)(x-4/3) |
+
0 - 0
+ |
|
Signe de 15x²-17x-4 |
+
0 - 0
+ |
D'après
le tableau de signe l'ensemble solution de cette inéquation est
] -1/5 ; 4/3 [
Résolution
de 9x²-12x+4 ³ 0
9x²-12x+4
= 9(x-2/3)² ce polynôme est toujours positif, l'ensemble des réels est
solution.
6°)
a) D'après le graphique il y deux solutions 0 et 3 (intersection de la courbe
avec l'axe des abscisses).
b)
Les solutions de l'équation -x²+3x=4 sont les abscisses des points
d'intersection de la courbe représentative de
la
fonction -x²+3x et de la droite d'équation y = 4.
Il
en est de même pour les deux autres équation intersection avec y = 2,25 et y =
1
En
lisant le graphique :
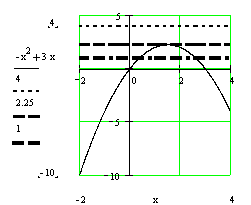
Dans
le premier cas il n'y a pas de solution
Dans
le second il y une solution pour x = 1,5 environ
Dans
le troisième cas il y a deux solutions x1 = 0,4 et x2 =
2,6
c)
En utilisant les formules de résolution :
-x²+3x
= 4 Pas de solution
-x²+3x
= 2,25 solution : x = 3/2
-x²+3x
= 1 solutions : x1 = (3-Ö5)/2»0,38 et x2 = (3
+ Ö5)/2»2,62