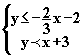7x
- 4 < 18
7x
- 4 + 4 < 18 + 4
7x
< 22
7x
/ 7 < 22 / 7
x < 22 / 7 L'intervalle de x solution de cette
inéquation est : ] -∞ ; 22/7 [
Exercice n°2
Pour
résoudre ces inéquations du second degré, il faut calculer le discriminant de
l'équation du second degré ( ax²
+ bx + c = 0 ) qui correspond et appliquer les règles
suivantes ( voir cours sur les équations et polynôme du second degré ) :
¶ Si le polynôme n'a pas de solutions, alors
pour tout réel x, le polynôme est du signe de a
· Si le polynôme a une ou deux solutions,
alors on effectue la factorisation du polynôme et on construit un tableau de
signe.
Résolution
de - 2 x² + 3 x + 8 > 0
Le
discriminant de l'équation -2x² + 3x + 8 = 0 est : Δ
= 3² -4 ´
(-2) ´
8 = 9 + 64 = 73
Il y a donc deux solutions : ![]()
![]()
-2x²
+ 3x + 8 se factorise donc de la manière suivante : -2(x - x1)(x - x2 )
On
a donc : -2x² + 3x + 8 = -2(x - x1)(x - x2 )
L'inéquation
du départ est donc équivalente à -2(x - x1)(x
- x2 ) > 0
Pour
étudier le signe de cet inéquation on dresse un
tableau de signe :
|
Valeurs de x |
x1 x2 |
|
Signe de x-x1 |
- 0 + |
|
Signe de x-x2 |
- 0 + |
|
Signe de (x-x1)(x-x2) |
+
0 - 0
+ |
|
Signe de -2x² + 3x + 8 |
-
0 + 0 - |
L'ensemble
solution est donc : ![]()
Résolution
de 4 x²+ 8 x + 15 > 0
Le
discriminant de l'équation 4x² + 8x + 15 = 0 est : Δ
= 8² -4 ´
2 ´ 15 = 64 - 120 = -56
Il
n'y a pas de solution à cette équation donc le polynôme 4x² + 8x + 15 est du
signe de 4 soit positif.
Quelque
soit la valeur de x on a 4x² + 8x + 15 > 0 ; L'ensemble solution est ] - ∞ ; + ∞ [
Résolution
de 13 x² - 2 x + 5 > 0
Le
discriminant de l'équation 13x² - 2x + 5 = 0 est : Δ
=(-2)² -4 ´ 13 ´ 5 = 4 - 260 = -256
Il
n'y a pas de solution à cette équation donc le polynôme 13x² - 2x + 5 est du signe de 13 soit positif.
Quelque
soit la valeur de x on a 13x² - 2x + 5> 0 ; L'ensemble solution est ] - ∞ ; + ∞ [.
Exercice n°3
![]() est
équivalent à
est
équivalent à ![]()
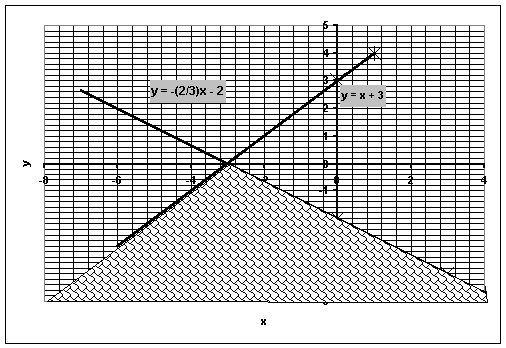
L'ensemble
des couples ( x ; y )
solution de ce système est donc l'ensemble des points dont les
coordonnées sont situées à la fois "au dessus" (droite comprise) de
la droite d'équation y = x + 1 et "en dessous" (droite comprise) de
la droite d'équation y = -x + 3
Il
faut tracer les deux droites :
y
= x + 1 passe par les points ( 0 ; 1 ) et ( 1 ; 2 ) par exemple
y
= -x + 3 passe par les points ( 0 ; 3 ) et ( 1 ; 2 )
par exemple
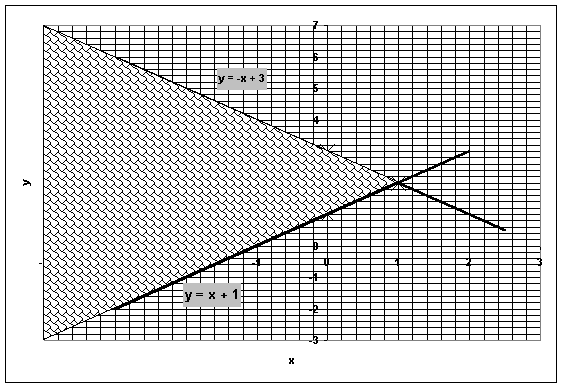
Les
solutions de ce système sont délimitées par la zone tuilées
sur le graphique.