Pré
requis : « Pythagore » ; « Développer un
prisme »
Niveau
4 : Les triangles rectangles :
« APPLIQUATION »
Recherche
et Calculs de dimensions dans un PRISME
DROIT.
Consignes : sur copie reproduire les figures ; mettre des couleurs pour
identifier les segments de droites dont on recherche la dimension.
|
Activité préalable : |
Données : |
|
|
|
|
|
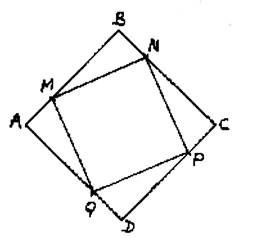
Soit le carré ABCD. On sait que : AB= 60 mm AM = BN = CP = DQ = 15 mm On demande : 1°) Par le tracé :mesurer les dimensions du carré MNPQ. 2°) par le calcul : déterminer les dimensions du carré MNPQ |
|
Soit les 3
prismes suivants :
|
N°1 |
Figure |
Données : |
|
|
|
|
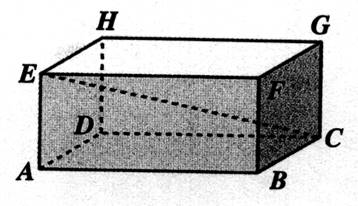
ADCB est la base du prisme.. Les dimensions
du parallélépipède rectangle sont : (en mm) L = 120
mm ; Largeur = 40 mm Hauteur = 30 mm 1°) Tracer les figures (faces) et déterminer par la mesure les dimensions EB = BG = EC = 2°) Déterminer par le calcul les dimensions EB = BG = EC = |
|
|
N°2 |
Figure |
Données : |
|
|
|
|
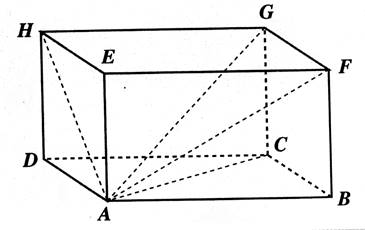
DCBA est la base du prisme.. Les dimensions du parallélépipède rectangle sont : (en mm) L = 100 mm ; Largeur = 40
mm ;Hauteur = 40 mm 1°) Faire un plan vue par
vue et mesurer la longueur : HA = ; GA
= ;FA
= ; CA = 2°) Déterminer par le calcul les dimensions |
|
|
N°3 |
Parallélépipède rectangle . |
Données : |
|
|
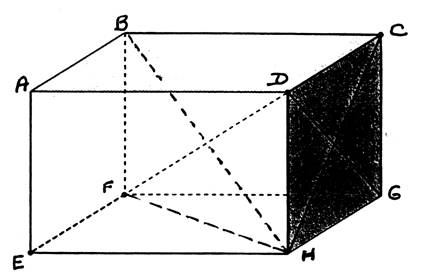
Les dimensions du prisme droit sont : 6 cm X 4 cm X 3 cm la vue de face mesure 6 cm par
3 cm. 1°) Tracer le prisme en
perspective cavalière. 2°) Tracer les vues et mesurer
les dimensions réelles de : ED =
; FH =
; HC = 3°) Déterminer par le
calcul les dimensions : ED =
; FH =
; HC = En plus : 4°) calculer la surface latérale du prisme. 5°) calculer la surface totale du prisme. 6°) Calculer le volume du prisme. 7°) Calculer la masse du prisme
( masse volumique = 1,2 kg / dm3 ;
g = 9,81 8°) Calculer la masse et le poids du prisme. |
|