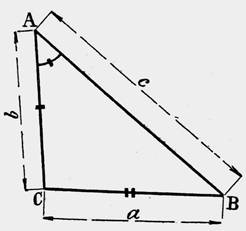
DOSSIER : LES RELATIONS entre les éléments d’un TRIANGLE QUELCONQUE.
Travaux auto formatifs. Sur : Résolution des triangles quelconques.
CONTROLE :
Citer les 3 relations que l’on utilise pour résoudre les triangles quelconques en trigonométrie
EVALUATION :
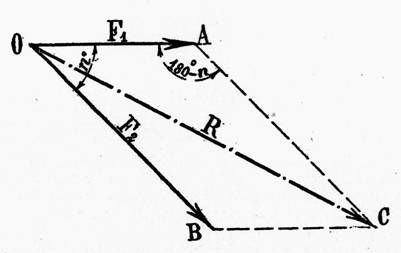
Application : On donne deux forces : si F1 = 15 N F 2 = 25 N et L’angle = 45° . 1°) Calculer la valeur de la résultante 2°) Donner la valeur de la direction de la résultante
Faire Les 4 EXERCICES types :
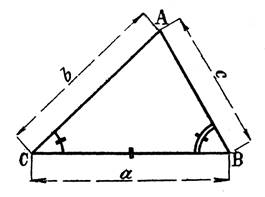
Premier cas : Résoudre un triangle quelconque dont on connaît un côté « a » et les deux angles adjacents et .
Les données sont : « a » = 83,25 m = 39° 30’ = 58° 20’		Les inconnues sont donc : « b » , « c » , et l’angle A.
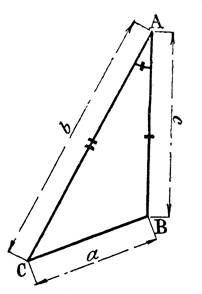
Deuxième cas : Résoudre un triangle quelconque dont on connaît deux côtés « b » et « c » et l’angle .
Les données sont : « b » = 160,60 m « c » = 112 , 90 m = 26° 15		Les inconnues sont donc : « a » =  ? = ? =  ?
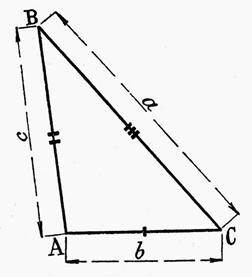
Troisième cas : Résoudre un triangle quelconque dont on connaît les trois côtés « a » , « b » et « c » .
Les données sont : « b » =  118 m « c » =  65 ,90 m « a » =  80,55 m		Les inconnues sont donc : = ? =  ? = ?
Quatrième cas : (deux exemples seront proposés : le premier débouche sur un ensemble de solutions . Le second exemple débouche sur deux ensembles de solutions possibles)
Résoudre un triangle quelconque dont on connaît deux côtés et l’angle opposé à l’un d’eux.
Les données : « a » « b » l’angle A.	Les inconnues sont : L’angle B ; L’angle C « c »
SERIE D’ EXERCICES sans corrigé :
I ) Résoudre un triangle quelconque connaissant :
Triangle 1
« a » = 728,5 m			« b » = ?			« c » = ?
= ?			= 34° 15’			= 58° 25’
Triangle 2
« a » = 164 , 30 m			« b » = ?			« c » = ?
= ?			= 48 ° 13’			= 54 ° 24 ‘
Triangle 3
« a » =			« b » =632 , 8 m			« c » = 340 , 5 m
= 35° 40’			=			=
Triangle 4
« a » =			« b » = 416,10 m			« c » = 802, 4 m
= 68° 24 ‘			=			=
Triangle 5
« a » = 153,20 m			« b » = 90 , 50 m			« c » = 162,30 m
=			=			=
Triangle 6
« a » = 146,15 m			« b » = 162, 25 m			« c » = 180, 75 m
=			=			=
Triangle 7
« a » = 124,75 m			« b » = 156,25 m			« c » =
= 42° 15’			=			=
Triangle 8
« a » = 219,65 m			« b » = 184, 45 m			« c » =
= 65° 25’			=			=
Calculer la hauteur AH d’un triangle ABC dans lequel on a : « a » = 4,25 m ; = 54° 40’ ; = 68°15’
Résoudre un triangle ABC inscrit dans une circonférence de rayon donné « R » = 0,125 m , sachant que les angles = 45° et = 60°
On donne un triangle ABC ; « a » = 2,75 m ; = 64° 30’ ; = 53° 20’ calculer 1°)le rayon « r » du cercle inscrit ; 2°) le rayon ra exinscrit dans l’angle .
INTERDISCIPLINARITE : mécanique.
1°) Un corps est soumis à l’action de deux forces concourantes ,, l’une de 1650 N l’autre de 3250 N . Ces forces font entre elles un angle de 56° 25’ . Calculer la valeur de la résultante des deux forces ainsi que son inclinaison par rapport aux deux composantes.
2° ) On veut remplacer l’action d’une force de 900 N par celles de deux forces ayant même point d’application que la première . L’une des deux forces est connues et vaut 380 N ; l’angle qu’elle fait avec celle de 900N est de 19° 20’ . On demande de calculer l’intensité de la deuxième force ainsi que l’angle des composantes.